谈谈卡尔曼滤波器
谈谈卡尔曼滤波器
文章目录
- 谈谈卡尔曼滤波器
- 概念
- 第一次使用
- 卡尔曼滤波器
- 状态观测器
- 卡尔曼滤波器基本思想
- 关于我
很早以前就听过卡尔曼滤波这个概念,但是一直没怎么接触过,而这个东西似乎又涉及挺广的,哪哪都能见到,哪哪都能用。今天想根据我了解的内容做一个整理。
概念
卡尔曼滤波(Kalman Filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
Kalman滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中,估计动态系统的状态。
常在控制、制导、导航、通讯等领域使用。目前已经发展了很多变体,扩展到更多领域,如计算机视觉。
第一次使用
斯坦利·施密特(Stanley Schmidt)首次实现了卡尔曼滤波器。卡尔曼在NASA埃姆斯研究中心访问时,发现他的方法对于解决阿波罗计划的轨道预测很有用,后来阿波罗飞船的导航电脑使用了这种滤波器。关于这种滤波器的论文由Swerling (1958), Kalman (1960)与 Kalman and Bucy (1961)发表。

卡尔曼滤波器
状态观测器
比如,你想要知道你喜欢的女生现在心情是好还是差,那你可以递给她一个小零食,假如她接受并笑了,说明她现在心情不差。这个过程就是状态观测。
状态观测可以帮助你估计你无法直接观察或者测量的信息。
一般用 x ^ \hat{x} x^来表示对 x x x的估计量。
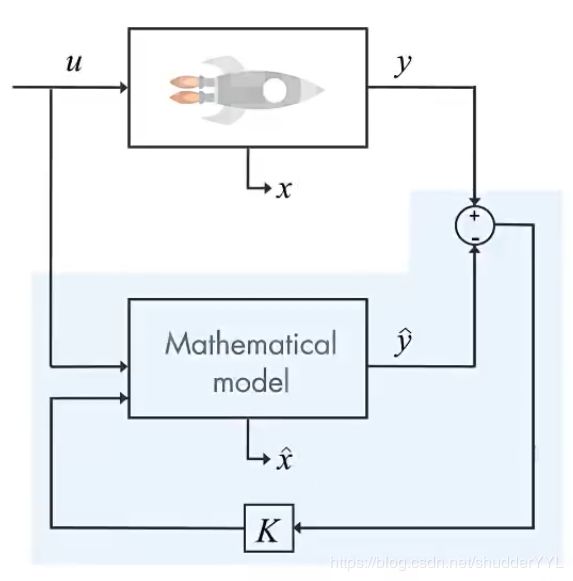
假如,有一架宇宙飞船在太空中飞行,我们需要监控喷气发动机的内部温度。如果温度太高,会损坏发动机,但是其内部温度本身就很高了,没有传感器可以被放在其内部直接测温,所以只能将传感器放在距离其不远处的外表面,放在那传感器不会被高温损坏,但是又可以测到一定的温度。
但这个温度并不代表发动机内部实际的温度,我们暂且将其标为 T e x t e r n a l T_{external} Texternal简写为 T e x t T_{ext} Text,而发动机内部的那个我们无法直接测量的实际温度我们将其标为 T i n t e r n a l T_{internal} Tinternal简写为 T i n T_{in} Tin。通过控制燃油流量来达到控制发动机内部温度的目的。
实际发动机内部写成状态方程的模样:
x ˙ = A x + B u y = C x \begin{alignedat}{2} &\dot{x}=Ax+Bu \\ &y=Cx \end{alignedat} x˙=Ax+Buy=Cx
这个 u u u是输入,表示发动机燃料流量。 y y y是输出,表示外测温度 T e x t T_{ext} Text。 x x x是观测量,表示观测温度 T i n T_{in} Tin。
我们的数学模型:
x ^ ˙ = A x ^ + B u y ^ = C x ^ \begin{alignedat}{2} &\dot{\hat{x}}=A\hat{x}+Bu \\ &\hat{y}=C\hat{x} \end{alignedat} x^˙=Ax^+Buy^=Cx^
因为数学模型的估计值肯定没法和实际值一样,中间就存在一个误差,我们的目标是将观测值 x ^ \hat{x} x^逐步逼近 x x x,从图1中可以看出,误差反馈回路中有一个 K K K,则:
x ˙ − x ^ ˙ = A ( x − x ^ ) + B u − B u + K ( y − y ^ ) e = x − x ^ e ˙ = x ˙ − x ^ ˙ y − y ^ = C e K ( y − y ^ ) = K ( C ( x − x ^ ) ) \begin{alignedat}{3} &\dot{x}-\dot{\hat{x}}=A(x-\hat{x})+Bu-Bu+K(y-\hat{y}) \\ &e=x-\hat{x} \\ &\dot{e}=\dot{x}-\dot{\hat{x}}\\ &y-\hat{y}=Ce\\ &K(y-\hat{y})=K(C(x-\hat{x})) \end{alignedat} x˙−x^˙=A(x−x^)+Bu−Bu+K(y−y^)e=x−x^e˙=x˙−x^˙y−y^=CeK(y−y^)=K(C(x−x^))
所以 e ˙ = ( A − K C ) e \dot{e}=(A-KC)e e˙=(A−KC)e,这个方程的解是一个指数函数 e ( t ) = e ( A − K C ) t e ( 0 ) e(t)=e^{(A-KC)t}e(0) e(t)=e(A−KC)te(0),
这就表示:
i f ( A − K C ) < 0 : t h e n e → 0 , a s t → ∞ , s o x ^ → x \begin{aligned} if (&A-KC)<0: \\ &then \enspace e \to 0,as\enspace t\to \infin,so \enspace \hat{x} \to x \end{aligned} if(A−KC)<0:thene→0,ast→∞,sox^→x
给观测器建立反馈回路的重要性在于,我们可以通过选择相应的控制器增益 K K K控制误差函数的衰减率。这里的 A A A一般不知道,所以无法控制误差衰减率的速度。使用反馈控制器可以更好地控制这些方程,并确保更快地消除错误。误差消除得越快,估算状态 x ^ \hat{x} x^收敛到 x x x的速度也就越快。
那么,选择 K K K的最佳方法,就是使用卡尔曼滤波器。
卡尔曼滤波器基本思想
假如,有一个自动驾驶汽车比赛,车里使用GSNN来测量汽车的位置,多支队伍分别在100种不同的地形上行驶1km,要求都要尽可能正好停在终点线上。比赛结束时,计算每支队伍的平均停车位置(AFP,Average Final Position)。具有最小误差方差(variance最小)和平均距离最接近1km(bias最小)的车队能获得冠军。
如果想要赢得比赛,那就不能完全依靠GSNN的数据,因为有时候卫星测的位置信息并不准确(尤其是在隧道、地下等场所,或者多云多雾的天气下)。除此之外,可以用卡尔曼滤波器来辅助估算汽车的位置。
如图3所示,我们可以构建一个简单的状态方程:
x k = A x k − 1 + B u k + w k y k = C x k + v k \begin{alignedat}{2} &x_k=Ax_{k-1}+Bu_k+w_k \\ &y_k=Cx_k+v_k \end{alignedat} xk=Axk−1+Buk+wkyk=Cxk+vk
这里可能有 k k k个输入,但输入 u k u_k uk都是速度(velocity)。输出 y k y_k yk是我们感兴趣的汽车的位置(position),观测的状态 x k x_k xk只有一个,是汽车的位置(position),这个状态正是我们测量的输出,也就是 y k = C x k + v k y_k=Cx_k+v_k yk=Cxk+vk,所以 C = 1 C=1 C=1。这里的 y k y_k yk是GSNN测得的,存在一定的误差,而且这种误差是随机变量,我们假设为 v k v_k vk。同样,还有过程误差(一般可以是外界环境对车速的影响),也是个随机变量,表示为 w k w_k wk。
这里的两个误差 v k v_k vk和 w k w_k wk我们不知道具体值,也没法测,但是我们可以用概率论中的各种表示它们,这些分布可以表示它们的平均属性。
假设:
v ∽ N ( 0 , R ) v\backsim N(0,R) v∽N(0,R), w ∽ N ( 0 , Q ) w\backsim N(0,Q) w∽N(0,Q),由于这是一个单输出系统,所以协方差矩阵 R = σ v 2 R=\sigma_v^2 R=σv2, Q = σ w 2 Q=\sigma_w^2 Q=σw2也就是方差。
同样,我们建立一个数学模型来对其进行估计。
卡尔曼滤波器将测量结果和预测结果相结合对汽车位置进行最优估计。
我先来解释一下图5,图5是从概率密度函数的角度,解释卡尔曼滤波器的工作原理。 x ^ k − 1 \hat{x}_{k-1} x^k−1是初始时刻的位置预测值,variance是方差,随着汽车的移动,进行到下一时刻 k k k,估计的不确定性增加,方差更大了。也许预测的位置 x k ^ \hat{x_k} xk^和实际测试的位置 y k y_k yk差得更多了,此时红色的线是测试的结果。用这二者共同表示真实的汽车位置,可见这个范围是很大的。有了预测和测试值,我们需要将其二者的信息进行整合,以便估计最优位置,可以通过将两个概率密度函数相乘得到,相乘的结果也是符合高斯分布,而该概率密度函数的平均值就是汽车位置的最优估计。
此处离散卡尔曼滤波器的方程是:
x k ^ = A x ^ k − 1 + B v k + K k ( y k − C ( A x ^ k − 1 + B u k ) ) \hat{x_k}=A\hat{x}_{k-1}+Bv_k+K_k(y_k-C(A\hat{x}_{k-1}+Bu_k)) xk^=Ax^k−1+Bvk+Kk(yk−C(Ax^k−1+Buk))
这就是卡尔曼滤波器的基本思想。