算法思想（五）——二叉搜索树

5.1 二分查找法 Binary Search

对于有序数列，才能使用二分查找法（排序的作用）（logn级别复杂度）

使用递归方式实现二分查找法
递归实现通常思维起来更容易，但在性能上会有略差。

//二分查找法，在有序数组arr中，查找target
//如果找到target，返回相应的索引index
//如果没有找到target，返回-1
template<typename T>
int binarySearch(T arr[],int n,T target)
{
    //在arr[l...r]中查找target
    int l=0,r=n-1;
    while(l<=r){
       //int mid =(l+r)/2;
       int mid = l+(r-l)/2;//避免溢出
       if(arr[mid]==target)
            return mid;

       if(target<arr[mid])
        //在arr[l....mid-1]中查找target
        r=mid-1;
       else
       //在arr[mid+1...r]中查找target
        l=mid+1;

    }
    return -1;

}

//用递归的方式写二分查找法
template<typename T>
int _binarySearch2(T arr[],int l,int r,T target)
{
    if(l>r) //递归结束条件
        return -1;

    int mid= l+(r-l)/2;

    if(arr[mid]==target)
        return mid;
    else if (target<arr[mid])
        return _binarySearch2(arr,l,mid-1,target);
    else
        return _binarySearch2(arr,mid+1,r,target);

}

template<typename T>
int binarySearch2(T arr[],int n,T target)
{
    return _binarySearch2(arr,0,n-1,target);
}

测试递归和非递归的二分查找的效率

#include
#include
#include

#include"BinarySearch.h"

//比较递归和非递归的二分查找的效率
//非递归算法在性能上有微弱优势
int main()
{
    int n= 1000000;
    int* a = new int[n];
    for(int i=0;i<n;i++)
        a[i]=i;

    //测试非递归二分查找法
    clock_t startTime = clock();

    // 对于我们的待查找数组[0...N)
    // 对[0...N)区间的数值使用二分查找，最终结果应该就是数字本身
    // 对[N...2*N)区间的数值使用二分查找，因为这些数字不在arr中，结果为-1
   for(int i=0;i<2*n;i++)
   {
       int v =binarySearch(a,n,i);
       if(i<n)
        assert(v==i);
       else
        assert(v==-1);
   }
   clock_t endTime = clock();
   cout<<"Binary Search(without Recursion):"<<double(endTime-startTime)/CLOCKS_PER_SEC<<" s"<<endl;


   // 测试递归的二分查找法
   startTime = clock();

    // 对于我们的待查找数组[0...N)
    // 对[0...N)区间的数值使用二分查找，最终结果应该就是数字本身
    // 对[N...2*N)区间的数值使用二分查找，因为这些数字不在arr中，结果为-1
   for( int i = 0 ; i < 2*n ; i ++ ){
        int v = binarySearch2(a, n, i);
        if( i < n )
            assert( v == i );
        else
            assert( v == -1 );
    }
    endTime = clock();
    cout << "Binary Search (Recursion): " << double(endTime - startTime) / CLOCKS_PER_SEC << " s"<<endl;

    delete[] a;

    return 0;
}

测试结果：

二分查找法的变种

两个非常重要的函数：floor和ceil（有的地方也成为lowerBound和upperBound）

为什么要使用这两个函数？
之前实现的二分查找法（上文），都是假设在这个数组中没有重复元素的，当然有重复元素时，依然能找到这个元素的索引，只不过这个元素可能在数组中出现过很多次，上文的二分查找无法找到具体哪个索引。

相应定义了两个函数，floor找到这个数字v在数组中第一次出现的位置。ceil是v最后一次出现的位置

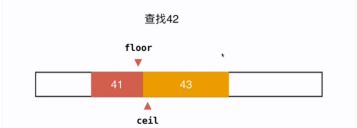
当在数组中查找的元素不存在的时候，（如查找42），上文的算法得到的是-1，但是定义floor和ceil后，如图，floor返回的是42之前的元素（41）的元素的最后一个位置，ceil返回的是42之后的元素（43）的第一个位置。

5.2 二分搜索树基础（Binary Search Tree）

---

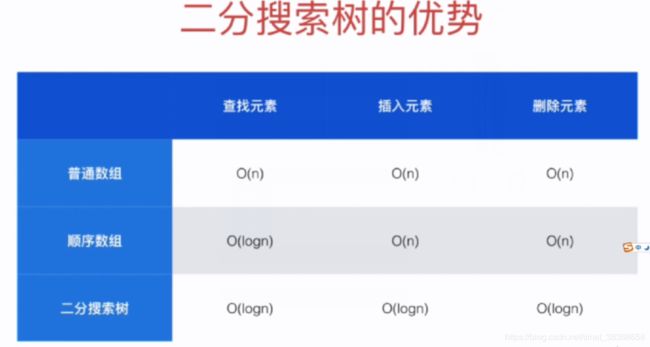
二分搜索树定义：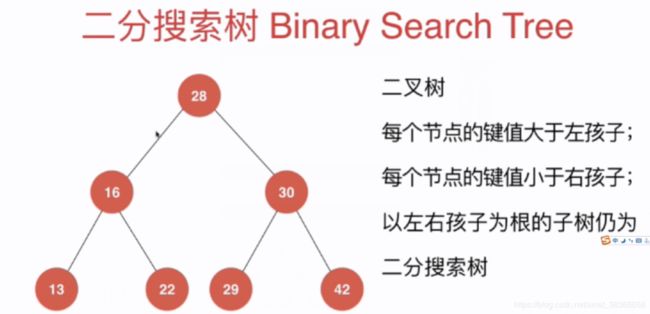
首先他依然是一颗二叉树

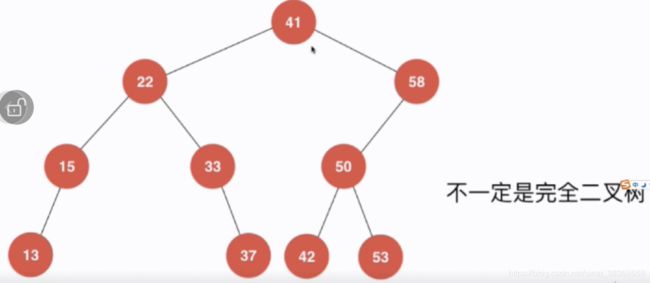
但是。二分搜索树不一定是一个完全二叉树，所以不能用数组，通常使用node结点表示key-value对，使用指针表示结点之间的关系。
[注]：上述结点的值为key的值

5-3 二分搜索树的节点插入

#ifndef BST_H_INCLUDED
#define BST_H_INCLUDED

#include
#include
#include

using namespace std;

template<typename Key,typename Value>
class BST{

private:
    struct Node {
        Key key;
        Value value;
        Node *left;
        Node *right;

        Node(Key key,Value value){
            this->key=key;
            this->value=value;
            this->left=this->right=NULL;
        }

    };

    Node *root;
    int count;

public:
    BST(){
        root = NULL;
        count =0;
    }
    ~BST(){
        //
    }
    int size(){
        return count;
    }

    bool isEmpty(){
        return count==0;
    }

    void insert(Key key,Value value){
        root = insert(root,key,value);
    }

    bool contain(Key key){

        return contain(root,key);
    }

    //使用Value* 使得当查找不存在的时候，可以返回空
    Value* search(Key key){
        return search(root,key);
    }


private:
    //递归定义的insert方法
    //向以node为根的二叉搜索树中，插入结点（key，value）
    //返回插入新节点后的二叉搜索树的根
    Node* insert(Node* node,Key key,Value value ){

        //递归到底的的情况
        if(node == NULL)
        {
            count++;
            return new Node(key,value);
        }

        if(key == node->key)
            node->value = value;
        else if(key<node->key)
            node->left = insert(node->left,key,value);
        else //key > node->key
            node->right = insert(node->right,key,value);

        return node;
    }

    //查看以node为根的二叉搜索树中是否包含键值为key的节点
    bool contain(Node* node, Key key){

        //递归到底的最基本的情况
        if(node==NULL)
        {
            return false;
        }

        if(key==node->key)
            return true;
        else if(key<node->key)
            return contain(node->left,key);
        else
            return contain(node->right,key);
    }

    //在以node为根的二叉搜索树中查找key所对应的value
    Value* search(Node* node,Key key){

        if(node==NULL)
            return NULL;

        if(key==node->key)
            return &(node->value);
        else if(key<node->key)
            return search(node->left,key);
        else
            return search(node->right,key);
    }
};



#endif // BST_H_INCLUDED

5-4 二分搜索树的查找

---

二分查找树的包含contain和查找search同质
如上述代码。