冒泡排序(Bubble Sort): 一种交换排序,它的基本思想是:两两比较相邻的关键字,如果反序则交换,直到没有反序的记录为止。
平实写冒泡排序,我都是这么写的:
- (void)logArray {
NSMutableArray * arr = @[@16,@1,@2,@9,@7,@12,@5,@3,@8,@13,@10].mutableCopy;
for (int i = 0; i < arr.count; i++) {
for (int j = i+1; j < arr.count; j++) {
if ([arr[i] intValue] < [arr[j] intValue]) {
[arr exchangeObjectAtIndex:i withObjectAtIndex:j];
}
}
[self logArr:arr];
}
}
//打印数组
- (void)logArr:(NSMutableArray * )array {
NSString * str = @"";
for (NSNumber * value in array) {
str = [str stringByAppendingString:[NSString stringWithFormat:@"%zd ",[value integerValue]]];
}
NSLog(@"%@",str);
}
//打印结果如下
16 1 2 9 7 12 5 3 8 13 10
16 13 1 2 7 9 5 3 8 12 10
16 13 12 1 2 7 5 3 8 9 10
16 13 12 10 1 2 5 3 7 8 9
16 13 12 10 9 1 2 3 5 7 8
16 13 12 10 9 8 1 2 3 5 7
16 13 12 10 9 8 7 1 2 3 5
16 13 12 10 9 8 7 5 1 2 3
16 13 12 10 9 8 7 5 3 1 2
16 13 12 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
查了定义后发现,这不算是标准的冒牌排序算法,因为它不满足“两两比较相邻”的冒泡排序思想,它更应该是最最简单的交换排序而已。它的思路是让每个关键字,都和它后面的一个关键字比较,如果小则交换。
它应该算是最容易写的排序代码了,不过这个简单易懂的代码是有缺陷的,观察后发现,每次排序只能确定一个位置,直到倒数第二次 末尾的最小值1才显示到最后,也就是说,这个算法的效率是非常低的。
正宗的冒泡排序算法:
- (void)logArrayFunction {
int count = 0;
int forcount = 0;
NSMutableArray * arr = @[@16,@1,@2,@9,@7,@12,@5,@3,@8,@13,@10].mutableCopy;
for (int i = 0; i < arr.count; i++) {
forcount++;
// 依次定位左边的
for (int j = (int)arr.count-2; j >= i; j--) {
count++;
if ([arr[j] intValue]< [arr[j+1] intValue]) {
[arr exchangeObjectAtIndex:j withObjectAtIndex:j+1];
}
}
[self logArr:arr];
}
NSLog(@"循环次数:%d",forcount);
NSLog(@"共%d次比较",count);
}
//打印如下
16 13 1 2 9 7 12 5 3 8 10
16 13 12 1 2 9 7 10 5 3 8
16 13 12 10 1 2 9 7 8 5 3
16 13 12 10 9 1 2 8 7 5 3
16 13 12 10 9 8 1 2 7 5 3
16 13 12 10 9 8 7 1 2 5 3
16 13 12 10 9 8 7 5 1 2 3
16 13 12 10 9 8 7 5 3 1 2
16 13 12 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
循环次数:11
共55次比较
/// 同样的道理,先定位右边:
int count = 0;
int forcount = 0;
NSMutableArray * arr = @[@16,@1,@2,@9,@7,@12,@5,@3,@8,@13,@10].mutableCopy;
for (int i = 0; i < arr.count; i++) {
forcount++;
for (int j = 0; j < arr.count-i-1; j++) {
count++;
if ([arr[j] integerValue] < [arr[j+1] integerValue]) {
[arr exchangeObjectAtIndex:j withObjectAtIndex:j+1];
}
}
[self logArr:arr];
}
NSLog(@"循环次数:%d",forcount);
NSLog(@"共%d次比较",count);
16 2 9 7 12 5 3 8 13 10 1
16 9 7 12 5 3 8 13 10 2 1
16 9 12 7 5 8 13 10 3 2 1
16 12 9 7 8 13 10 5 3 2 1
16 12 9 8 13 10 7 5 3 2 1
16 12 9 13 10 8 7 5 3 2 1
16 12 13 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
循环次数:11
共55次比较
冒泡排序的优化:
设想如果待排序的序列是{2,1,3,4,5,6,7,8,9},也就是说,2和1交换后就属于正常的排序结果了,但是之后的大量比较还是大大多余了。所以如果循环一次后如果没有数据交换,这就说明此序列已经有序,不需要再继续后面的循环判断工作了,为了实现这一想法,我们需要改进下代码,增加个BOOL变量flag来实现这一算法的改进。
- (void)logArrayFunctionNice {
int count = 0;
int forcount = 0;
BOOL flag = YES;
NSMutableArray * arr = @[@16,@1,@2,@9,@7,@12,@5,@3,@8,@13,@10].mutableCopy;
for (int i = 0; i < arr.count && flag; i++) {
forcount++;
flag = NO;
for (int j = (int)arr.count-2; j >= i; j--) {
count++;
if ([arr[j] intValue]< [arr[j+1] intValue]) {
[arr exchangeObjectAtIndex:j withObjectAtIndex:j+1];
flag = YES;
}
}
[self logArr:arr];
}
NSLog(@"循环次数:%d",forcount);
NSLog(@"共%d次比较",count);
}
//打印
16 13 1 2 9 7 12 5 3 8 10
16 13 12 1 2 9 7 10 5 3 8
16 13 12 10 1 2 9 7 8 5 3
16 13 12 10 9 1 2 8 7 5 3
16 13 12 10 9 8 1 2 7 5 3
16 13 12 10 9 8 7 1 2 5 3
16 13 12 10 9 8 7 5 1 2 3
16 13 12 10 9 8 7 5 3 1 2
16 13 12 10 9 8 7 5 3 2 1
16 13 12 10 9 8 7 5 3 2 1
循环次数:10
共45次比较
冒泡排序复杂度分析
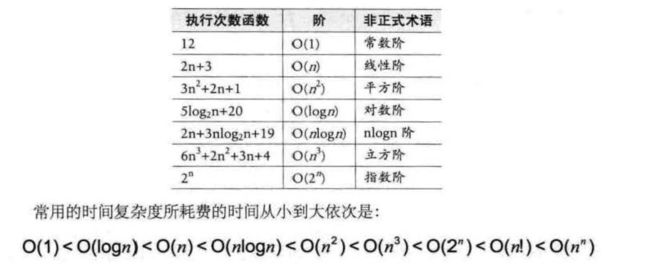
分析一下它的时间复杂度。当最好的情况,也就是要排序的本身就是有序的,那么我们比较次数,根据最后改进的代码,可以推断出就是n-1次的比较,没有数据交换,时间复杂度为O(n),当最坏的情况,即待排序表示逆序的情况,此时需要比较1+2+3+...+(n-1) = n(n-1)/2次,并作等数量级的记录移动,因此,总的时间复杂度为O(n²)。
备注:
时间性能 = 对比次数 + 是否移动
时间复杂度表:
下一篇:iOS算法总结-选择排序