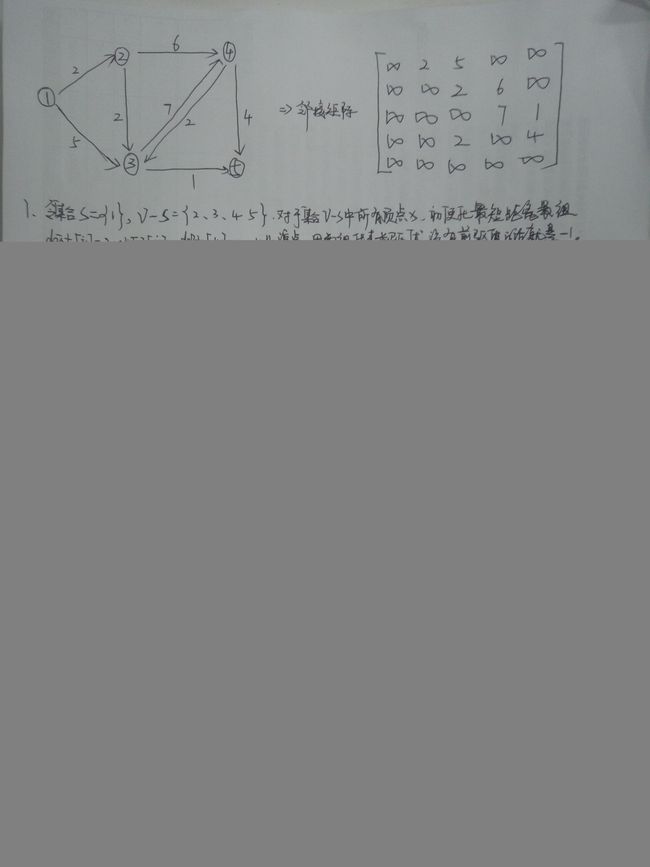
贪心算法之最短路径问题(Dijkstra算法)
1、问题
一个求单源最短路径的问题。给定有向带权图 G =(V, E ),
其中每条边的权是非负实数。此外,给定 V 中的一个顶点,
称为源点。现在要计算从源到所有其他各顶点的最短路径长
度,这里路径长度指路上各边的权之和。
其中每条边的权是非负实数。此外,给定 V 中的一个顶点,
称为源点。现在要计算从源到所有其他各顶点的最短路径长
度,这里路径长度指路上各边的权之和。
2、分析
3、代码实现
1、普通C++实现
#include
#include
#include
#include
using namespace std;
/*
一定要记得如果初始化矩阵的话,肯定需要一个变量保存长和宽的最大值,
如果看到权重的话,肯定是需要有个变量保存最大值的权重
*/
//城市的节点数目的最大值
const int MAX_CITY_NUM = 100;
//节点权值的最大值
const int MAX_POLICY = 1e7;
//初始化权重矩阵
int map[MAX_CITY_NUM][MAX_CITY_NUM];
//源点到各个顶点的最短具体数组
int dist[MAX_CITY_NUM];
//下标表示当前节点值,然后值保存为上个节点值
int p[MAX_CITY_NUM];
//城市的节点数目和线段的个数
int n, m;
//是否加入集合S,如果在集合S里面的话,值为true,否则在集合S-V里面,值为false;
bool flag[MAX_CITY_NUM];
//Dijkstra算法
void dijkstra(int start)
{
//初始化和源点相连的顶点进行初始化
for (int i = 1; i <= n; ++i)
{
//先把前节点都设置成false
flag[i] = false;
//先把和源点关联在一起的进行初始化,如果没有源点关联在一起的话
//就设置为权重的最大值,如果我在下面的条件里面判断,部分节点的权重
//可能为0,后面可能有问题
dist[i] = map[start][i];
if (dist[i] != MAX_POLICY)
{
//dist[i] = map[start][i];
p[i] = start;
}
else
{
p[i] = -1;
}
}
flag[start] = true;
dist[start] = 0;
//一开始,我忘记了dist[i]里面没有和源点关联的值应该是MAX_POLICY
//然后我也忘记了p[i]里面如果没有放值的话应该初始化为-1
//然后我也忘记了dist[start]=0,源点到源点的权重是0
//上面s集合里面只有源点,我们接下来需要在s集合里面添加其它的顶点,
for (int i = 1; i <= n; ++i)
{
//t保存我们每次找到的最小节点权重,然后min_dist用来每次保存最小的节点权重,然后每次更新这个数据
int min_dist = MAX_POLICY, t = start;
//先在V-S集合里面找到dist[i]里面权重最小的数据,然后把顶点加入s集合
for (int j = 1; j <= n; j++)
{
//这里需要得到最小的dist[j],所以我们这里不能用!=,必须用<
if (dist[j] < min_dist && !flag[j])
{
min_dist = dist[j];
t = j;
}
}
//我们发现程序退出的时候,p[j]里面只有源点的值是-1,其它的值都不是-1
//所以我们需要在循环里面打个标记,如果进去了,说明不能退出,如果没有进去
//这个临时变量t和之前的临时变量的值是一样,我们就跳出循环
if (t == start) return;
//找到之后我们需要先设置flag[j]为true
flag[t] = true;
//加入到s集合之后,如果发现新权重比在dist[i]里面要小,就需要更新dist[i]
for (int j = 1; j <= n; j++)
{ //C++里面false的值是0,不是-1,true的值是1,以后一定不能忘记
if (map[t][j] < MAX_POLICY && !flag[j])
{
if (dist[j] > (dist[t] + map[t][j]))
{
//更新新的定点权重
dist[j] = dist[t] + map[t][j];
//找到之后要记得设置之前的顶点
p[j] = t;
}
}
}
}
}
//打印出每个顶点的路径,这里值保存了前一个节点的key
//所以我们需要用到栈的特点,先进后出
void showProcess(int start)
{
int value;
stack stack;
for (int i = 1; i <= n; ++i)
{
value = p[i];
std::cout << "源点"<< start << "到"<< i << "的路径是";
while (value != -1)
{
stack.push(value);
value = p[value];
}
while (!stack.empty())
{
//pop函数是出来栈,没有返回值,先取出栈顶值,然后出栈
int node = stack.top();
stack.pop();
std::cout << node << "-";
}
std::cout << i << "最短距离为" << dist[i] << std::endl;
}
}
int main()
{
//定点u到定点v的权重是w, 然后输入的起始地点是start;
int u, v, w, start;
std::cout << "请输入城市的节点个数" << std::endl;
std::cin >> n;
if (n <= 0)
{
std::cout << "输入的城市节点个数因该大于0" << std::endl;
return -1;
}
std::cout << "请输入城市之间线路的个数" << std::endl;
std::cin >> m;
if (m <= 0)
{
std::cout << "输入的城市之前的线路个数不能小于0" << std::endl;
return -1;
}
//邻接举证的初始化,默认都为最大值,注意这里下标都是从1开始
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
map[i][j] = MAX_POLICY;
}
}
std::cout << "请输入城市顶点到城市顶点之前的权重" << std::endl;
//这里也可以使用while(--m),因为不涉及到用i
for (int i = 0; i < m; ++i)
{
std::cin >> u >> v >> w;
if (u > n || v > n)
std::cout << "您输入的定点有误" << std::endl;
//如果2次输入一样顶点,那么取最小的
map[u][v] = min(map[u][v], w);
}
std::cout << "请输入小明的位置" << std::endl;
//请输入起始的顶点
std::cin >> start;
if (start < 0 || start > n)
{
std::cout << "输入的起始城市定点有误" << std::endl;
return 0;
}
dijkstra(start);
std::cout << "小明所在的位置 " << start << std::endl;
for (int i = 1; i <= n; ++i)
{
std::cout << "小明(" << start << ")要去的位置是" << i;
if (dist[i] == MAX_POLICY)
std::cout << "无路可到" << std::endl;
else
std::cout << "最短距离为" << dist[i] << std::endl;
}
showProcess(start);
return 0;
}
2、类C++实现
#include
#include
#include
#include
using namespace std;
//城市的节点数目的最大值
const int MAX_CITY_NUM = 100;
//节点权值的最大值
const int MAX_POLICY = 1e7;
/*
一定要记得如果初始化矩阵的话,肯定需要一个变量保存长和宽的最大值,
如果看到权重的话,肯定是需要有个变量保存最大值的权重
*/
class Dijkstra
{
public:
//初始化工作
void init();
//dijkstra算法
void dijkstra();
//显示源点到其它顶点的经过的顶点
void showProcess();
//显示源点到各个顶点的最小权重
void showMinPolicy();
private:
//城市的节点数目和线段的个数和起始位置
int n, m, start;
//初始化权重矩阵
int map[MAX_CITY_NUM][MAX_CITY_NUM];
//源点到各个顶点的最短具体数组
int dist[MAX_CITY_NUM];
//下标表示当前节点值,然后值保存为上个节点值
int p[MAX_CITY_NUM];
//是否加入集合S,如果在集合S里面的话,值为true,否则在集合S-V里面,值为false;
bool flag[MAX_CITY_NUM];
};
//Dijkstra算法
void Dijkstra::dijkstra()
{
//初始化和源点相连的顶点进行初始化
for (int i = 1; i <= n; ++i)
{
//先把前节点都设置成false
flag[i] = false;
//先把和源点关联在一起的进行初始化,如果没有源点关联在一起的话
//就设置为权重的最大值,如果我在下面的条件里面判断,部分节点的权重
//可能为0,后面可能有问题
dist[i] = map[start][i];
if (dist[i] != MAX_POLICY)
{
//dist[i] = map[start][i];
p[i] = start;
}
else
{
p[i] = -1;
}
}
flag[start] = true;
dist[start] = 0;
//一开始,我忘记了dist[i]里面没有和源点关联的值应该是MAX_POLICY
//然后我也忘记了p[i]里面如果没有放值的话应该初始化为-1
//然后我也忘记了dist[start]=0,源点到源点的权重是0
//上面s集合里面只有源点,我们接下来需要在s集合里面添加其它的顶点,
for (int i = 1; i <= n; ++i)
{
//t保存我们每次找到的最小节点权重,然后min_dist用来每次保存最小的节点权重,然后每次更新这个数据
int min_dist = MAX_POLICY, t = start;
//先在V-S集合里面找到dist[i]里面权重最小的数据,然后把顶点加入s集合
for (int j = 1; j <= n; j++)
{
//这里需要得到最小的dist[j],所以我们这里不能用!=,必须用<
if (dist[j] < min_dist && !flag[j])
{
min_dist = dist[j];
t = j;
}
}
//我们发现程序退出的时候,p[j]里面只有源点的值是-1,其它的值都不是-1
//所以我们需要在循环里面打个标记,如果进去了,说明不能退出,如果没有进去
//这个临时变量t和之前的临时变量的值是一样,我们就跳出循环
if (t == start) return;
//找到之后我们需要先设置flag[j]为true
flag[t] = true;
//加入到s集合之后,如果发现新权重比在dist[i]里面要小,就需要更新dist[i]
for (int j = 1; j <= n; j++)
{ //C++里面false的值是0,不是-1,true的值是1,以后一定不能忘记
if (map[t][j] < MAX_POLICY && !flag[j])
{
if (dist[j] > (dist[t] + map[t][j]))
{
//更新新的定点权重
dist[j] = dist[t] + map[t][j];
//找到之后要记得设置之前的顶点
p[j] = t;
}
}
}
}
}
//打印出每个顶点的路径,这里值保存了前一个节点的key
//所以我们需要用到栈的特点,先进后出
void Dijkstra::showProcess()
{
int value;
stack stack;
for (int i = 1; i <= n; ++i)
{
value = p[i];
std::cout << "源点"<< start << "到"<< i << "的路径是";
while (value != -1)
{
stack.push(value);
value = p[value];
}
while (!stack.empty())
{
//pop函数是出来栈,没有返回值,先取出栈顶值,然后出栈
int node = stack.top();
stack.pop();
std::cout << node << "-";
}
std::cout << i << "最短距离为" << dist[i] << std::endl;
}
}
void Dijkstra::init()
{
//定点u到定点v的权重是w, 然后输入的起始地点是start;
int u, v, w;
std::cout << "请输入城市的节点个数" << std::endl;
std::cin >> n;
if (n <= 0)
{
std::cout << "输入的城市节点个数因该大于0" << std::endl;
return;
}
std::cout << "请输入城市之间线路的个数" << std::endl;
std::cin >> m;
if (m <= 0)
{
std::cout << "输入的城市之前的线路个数不能小于0" << std::endl;
return;
}
//邻接举证的初始化,默认都为最大值,注意这里下标都是从1开始
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
map[i][j] = MAX_POLICY;
}
}
std::cout << "请输入城市顶点到城市顶点之前的权重" << std::endl;
//这里也可以使用while(--m),因为不涉及到用i
for (int i = 0; i < m; ++i)
{
std::cin >> u >> v >> w;
if (u > n || v > n)
std::cout << "您输入的定点有误" << std::endl;
//如果2次输入一样顶点,那么取最小的
map[u][v] = min(map[u][v], w);
}
std::cout << "请输入小明的位置" << std::endl;
//请输入起始的顶点
std::cin >> start;
if (start < 0 || start > n)
{
std::cout << "输入的起始城市定点有误" << std::endl;
return;
}
}
void Dijkstra::showMinPolicy()
{
std::cout << "小明所在的位置 " << start << std::endl;
for (int i = 1; i <= n; ++i)
{
std::cout << "小明(" << start << ")要去的位置是" << i;
if (dist[i] == MAX_POLICY)
std::cout << "无路可到" << std::endl;
else
std::cout << "最短距离为" << dist[i] << std::endl;
}
}
int main()
{
Dijkstra dij;
dij.init();
dij.dijkstra();
dij.showMinPolicy();
dij.showProcess();
return 0;
} 4、运行结果和时间复杂度和空间复杂度
请输入城市的节点个数
5
请输入城市之间线路的个数
11
请输入城市顶点到城市顶点之前的权重
1 5 12
5 1 8
1 2 16
2 1 29
5 2 32
2 4 13
4 2 27
1 3 15
3 1 21
3 4 7
4 3 19
请输入小明的位置
5
小明所在的位置 5
小明(5)要去的位置是1最短距离为8
小明(5)要去的位置是2最短距离为24
小明(5)要去的位置是3最短距离为23
小明(5)要去的位置是4最短距离为30
小明(5)要去的位置是5最短距离为0
源点5到1的路径是5-1最短距离为8
源点5到2的路径是5-1-2最短距离为24
点5到3的路径是5-1-3最短距离为23
源点5到4的路径是5-1-3-4最短距离为30
源点5到5的路径是5最短距离为0时间复杂度O(n2),空间复杂的O(n);
5、总结
1、 最短路径我们采用贪心算法,每次找S-V集合里面最小权重得放到S集合,然后再找S集合里面零边的权重,是否更新数组的权重
2、我们用 for循环的时候,如果不涉及使用i,比如while(--m){}和for(int i = 0; i < m; ++i)等效
3、初始化的时候,要记得先把所有的dist[i]设置位最大值,然后还有所有得flag[i]为false,还有就是p[i]为-1
4、我们下次遇到问题,比如把集合数据拉到另外一个集合得时候,我们要记得构筑flag[i]来标识,比如true在一个集合,false代表另外一个集合
5、
当一个数组的value保存得值是,另外一个数组的key,也就是题目中的p[i],保持着前驱节点,这个时候我们需要用栈(stack),先push,然后pop处理,以后一定要有这个思想
6、在C++里面,我们把常量放在类的外面,然后全局变量,全局可以使用,如果在都在类方法里面使用的话,我们也可以把全局变量作为类的私有变量
7、C++里面尽量用头文件#include ,不要用#include
8、获取集合里面最小权重,我们可以先定义一个变量,默认最大值,然后通过for循环遍历获取权重,判断每次是否小于这个变量,遇到小的就跟新这个变量,就是这个比较小的权值。
9、这个问题跳出循环,我们分析,最后S-V集合里面没有数据,也就是说flag里面变成了true,所以我们先定义一个变量节点为源点,然后通过for循环里面找,如果发现都不匹配条件,(只有匹配条件才更新变量节点),然后最后发现变量节点依然是源点,我们就return.