房价预测解决方案
一、解决方案概述
1.1项目介绍与问题概述
请求买家描述他们的梦想家园,同时项目给出维79特征向量用来描述(几乎)爱荷华州Ames住宅的每一个方面。比赛挑战的就是你预测每个家庭的最终价格。
问题转换为回归问题,评价标准时RMSE,从MSSubClass,MSZoning,LotFrontage等特征提取新的特征。考虑到评价指标是RMSE,本质是一个回归问题,模型融合时候可以使用多个回归模型进行stacker。
1.2项目总体思路
本文首先从数据清洗开始,其次进行特征工程,再进行特征选择,再模型设计与分析。
二、数据清洗
2.1缺失数据处理
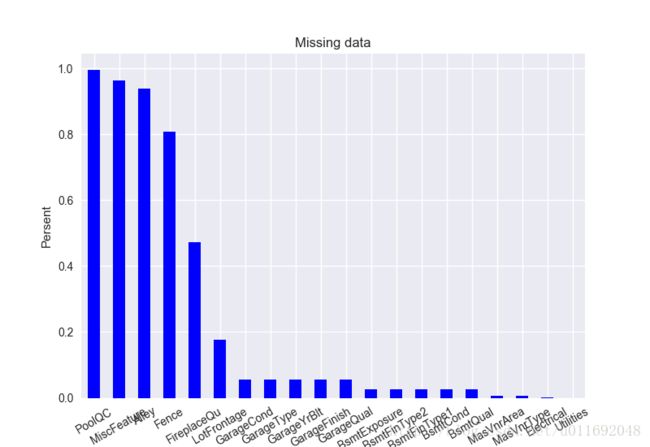
缺失数据意味着样本大小的缩减,影响分析。除此之外,以实质性的角度来说,需要保证对缺失数据的处理不会出现偏离或隐藏任何难以忽视的真相。按列统计缺失值个数,统计缺失值的属性和相应的缺失比率。
其中特征PoolQC,MiscFeature,Alley,Fence,FireplaceQu,LotFrontage缺失率大于10%,这6维数据可以直接丢掉。
2.2剔除常变量
原始数据中针对竖直型特征,通过计算每个数值型特征的标准差,剔除部分变化很小的特征。这些变化很小的特征意味着区分度很低,可以直接清除掉。
| KitchenAbvGr |
0.220338 |
| BsmtHalfBath |
0.238753 |
| HalfBath |
0.502885 |
| BsmtFullBath |
0.518911 |
| FullBath |
0.550916 |
| Fireplaces |
0.644666 |
| GarageCars |
0.747315 |
| BedroomAbvGr |
0.815778 |
| OverallCond |
1.112799 |
| YrSold |
1.328095 |
| OverallQual |
1.382997 |
| TotRmsAbvGrd |
1.625393 |
| MoSold |
2.703626 |
针对数值特征,去除方差较小的特征便于后续的特征工程。
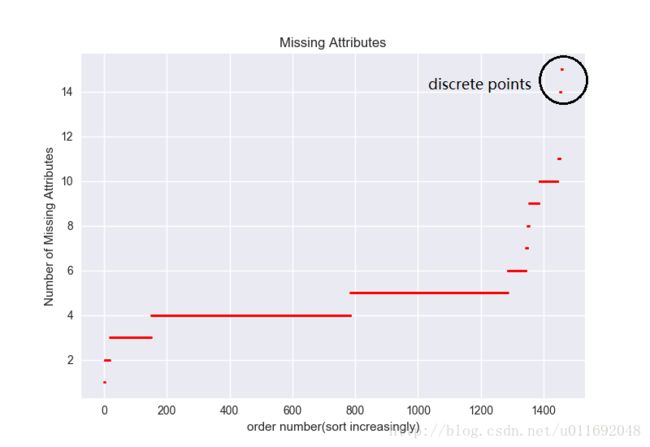
2.3剔除离群点
在样本空间中与其他样本点的一般行为或特征不一致的点称为离群点,考虑到离群点的异常特征可能是多维度的组合,我们通过分析样本属性的缺失值个数,剔除极少量的离群点。三、特征工程
进行特征工程,那么就要先对数据进行分析,分析数据之间的联系,数据的分布,数据的类型等。
l 房价分布
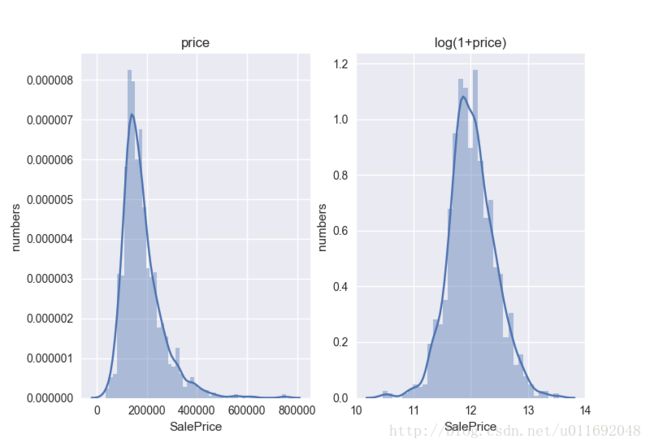
针对最重要的分布,绘制出房价的分布。
计算房价的偏度和峰度值Skewness: 1.882876,Kurtosis: 6.536282。可以发现label本身并不平滑,为了分类器的学习更加准确,首先把label给“平滑化”(正态化)。这里,用numpy中的log1p函数进行平滑。
1、相关变量分析
分别分析SalePrice,OverallQual,GrLivArea,GarageCars,TotalBsmtSF, FullBath和YearBuilt之间的关系,绘制相关性曲线,如下图所示。
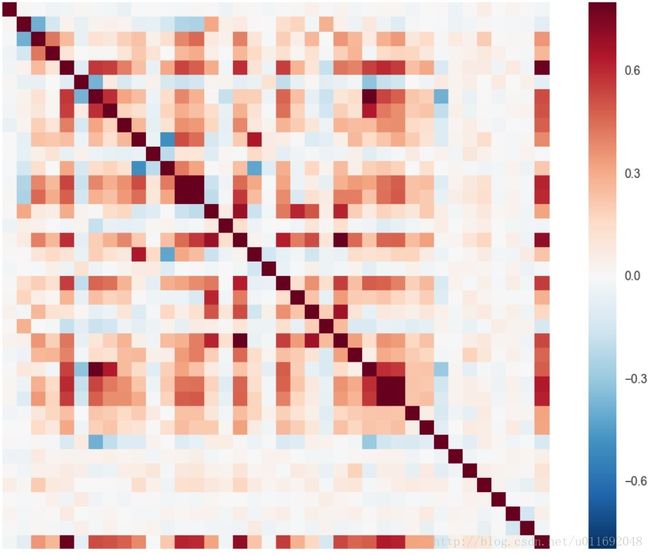
同时统计SalePrice和各个特征的相关系数矩阵,可以发现SalePrice和那些变量的相关性更强。如下图所示:
2、变量转换
首先注意到MSSubClass的值其实应该是一个category,需要对这些数字附后改成object形式,在进行one-hot编码。
3、缺失数据
处理数值特征时,发现数据存在缺失,前面已经数据清理中已经清除部分缺失数据,对于数据的缺失这里的处理办法是用平均值进行代替。
4、标准化数据
因为是做回归分类器,需要将源数据放在一个标准分布内,不要让数据之间的差距太大,因此需要对数据进行标准化处理。
四、特征选择
在特征工程部分,构建了一系列位置信息相关的特征、组合特征、成交时间特征、排序特征、类别稀疏特征相关的特征等,,这么多维特征一方面可能会导致维数灾难,另一方面很容易导致过拟合,需要做降维处理,降维方法常用的有如 PCA,t-SNE 等,这类方法的计算复杂度比较高。并且根据以往经验,在数据挖掘类的比赛中,PCA或 t-SNE 效果往往不好。除了采用降维算法之外,也可以通过特征选择来降低特征维度。
特征选择的方法很多:最大信息系数(MIC)、皮尔森相关系数(衡量变量间的线性相关性)、正则化方法(L1,L2)、基于模型的特征排序方法。比较高效的是最后一种,即基于学习模型的特征排序方法,这种方法有一个好处:模型学习的过程和特征选择的过程是同时进行的,因此采用这种方法,基于xgboost来做特征选择,xgboost模型训练完成后可以输出特征的重要性,据此我们可以保留 Top N个特征,从而达到特征选择的目的。
五、模型设计与分析
5.1 XGBoost
xgboost 的全称eXtreme Gradient Boosting。正如其名,它是Gradient Boosting Machine的一个c++实现,作者为正在华盛顿大学研究机器学习的大牛 陈天奇 。他在研究中深感自己受制于现有库的计算速度和精度,因此在一年前开始着手搭建xgboost项目,并在去年夏天逐渐成型。xgboost最大的特点在于,它能够自动利用CPU的多线程进行并行,同时在算法上加以改进提高了精度。
5.2 ExtraTreesRegressor
它适合于数据集的各种子样本上的多个随机决策树(又称额外树),并使用平均来提高预测精度和控制过拟合。
5.3 RandomForestRegressor
随机森林是一种元估计,适合于数据集的各种子样本上的多个分类决策树,并使用平均来提高预测精度和控制过拟合。子样本大小与原始输入样本大小始终相同,但如果bootstrap = True(默认),则样本将以替换方式绘制。
5.4 Ridge
该模型解决了一个回归模型,其中损失函数是线性最小二乘函数,正则化由l2范数给出。也称为岭回归或Tikhonov正则化。该估计器内置了对多变量回归的支持。
5.5 Lasso
LASSO由1996年Robert Tibshirani首次提出,全称Least absolute shrinkage and selection operator。该方法是一种压缩估计。它通过构造一个罚函数得到一个较为精炼的模型,使得它压缩一些系数,同时设定一些系数为零。因此保留了子集收缩的优点,是一种处理具有复共线性数据的有偏估计。
5.6 多模型Stack
在 Kaggle 等高水平的数据挖掘大赛中,诸多冠军队伍都会使用多模型融合技术,比如blending ensemble 和 stack ensemble 技术,因为单个模型的结果不够理想,如果想得到更好的结果,需要把很多单个模型的结果融合在一起,这就是一种 ensemble 技术。在这个比赛中选择stack ensemble的ensemble方式。主要融合效果较好5个模型:Xgboost,ExtraTreesRegressor,RandomForestRegressor,Ridge,Lasso。
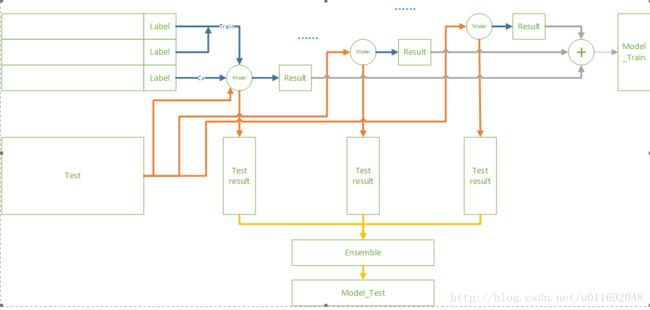
Stack过程是过程主要根据 CV过程将 train 数据集拆分成子训练集 train_train和子验证数据集 train_valid,通过每次对train_train进行训练分别对train_valid和test数据集进行预测train_valid_pred和test_pred结果,将每个模型CV产生的train_valid_pred。拼 接 成 train_pred ,对test_pred取 平 均 生 成test_pred_mean。这里假设分为3折,针对一个模型的示意图如下图所示5.7模型融合
通过5.6节可知,一个模型stack产生的Model_Test和Model_Train,这里考虑5个模型,在将5个Model_Train作为一个5维特征,原始数据的标签作为训练标签,再一次进行训练Xgboost。5个模型生成的Model_Test作为测试样本的5维特征。训练的示意图如下图所示:import pandas as pd
import numpy as np
from scipy.stats import skew
import xgboost as xgb
from sklearn.cross_validation import KFold
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import Ridge, RidgeCV, ElasticNet, LassoCV, Lasso
from math import sqrt
TARGET = 'SalePrice'
NFOLDS = 5
SEED = 0
NROWS = None
SUBMISSION_FILE = '../input/sample_submission.csv'
## Load the data ##
train = pd.read_csv("../input/train.csv")
test = pd.read_csv("../input/test.csv")
ntrain = train.shape[0]
ntest = test.shape[0]
## Preprocessing ##
y_train = np.log(train[TARGET]+1)
train.drop([TARGET], axis=1, inplace=True)
all_data = pd.concat((train.loc[:,'MSSubClass':'SaleCondition'],
test.loc[:,'MSSubClass':'SaleCondition']))
#log transform skewed numeric features:
numeric_feats = all_data.dtypes[all_data.dtypes != "object"].index
skewed_feats = train[numeric_feats].apply(lambda x: skew(x.dropna())) #compute skewness
skewed_feats = skewed_feats[skewed_feats > 0.75]
skewed_feats = skewed_feats.index
all_data[skewed_feats] = np.log1p(all_data[skewed_feats])
all_data = pd.get_dummies(all_data)
#filling NA's with the mean of the column:
all_data = all_data.fillna(all_data.mean())
#creating matrices for sklearn:
x_train = np.array(all_data[:train.shape[0]])
x_test = np.array(all_data[train.shape[0]:])
kf = KFold(ntrain, n_folds=NFOLDS, shuffle=True, random_state=SEED)
class SklearnWrapper(object):
def __init__(self, clf, seed=0, params=None):
params['random_state'] = seed
self.clf = clf(**params)
def train(self, x_train, y_train):
self.clf.fit(x_train, y_train)
def predict(self, x):
return self.clf.predict(x)
class XgbWrapper(object):
def __init__(self, seed=0, params=None):
self.param = params
self.param['seed'] = seed
self.nrounds = params.pop('nrounds', 250)
def train(self, x_train, y_train):
dtrain = xgb.DMatrix(x_train, label=y_train)
self.gbdt = xgb.train(self.param, dtrain, self.nrounds)
def predict(self, x):
return self.gbdt.predict(xgb.DMatrix(x))
def get_oof(clf):
oof_train = np.zeros((ntrain,))
oof_test = np.zeros((ntest,))
oof_test_skf = np.empty((NFOLDS, ntest))
for i, (train_index, test_index) in enumerate(kf):
x_tr = x_train[train_index]
y_tr = y_train[train_index]
x_te = x_train[test_index]
clf.train(x_tr, y_tr)
oof_train[test_index] = clf.predict(x_te)
oof_test_skf[i, :] = clf.predict(x_test)
oof_test[:] = oof_test_skf.mean(axis=0)
return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1)
et_params = {
'n_jobs': 16,
'n_estimators': 100,
'max_features': 0.5,
'max_depth': 12,
'min_samples_leaf': 2,
}
rf_params = {
'n_jobs': 16,
'n_estimators': 100,
'max_features': 0.2,
'max_depth': 12,
'min_samples_leaf': 2,
}
xgb_params = {
'seed': 0,
'colsample_bytree': 0.7,
'silent': 1,
'subsample': 0.7,
'learning_rate': 0.075,
'objective': 'reg:linear',
'max_depth': 4,
'num_parallel_tree': 1,
'min_child_weight': 1,
'eval_metric': 'rmse',
'nrounds': 500
}
rd_params={
'alpha': 10
}
ls_params={
'alpha': 0.005
}
xg = XgbWrapper(seed=SEED, params=xgb_params)
et = SklearnWrapper(clf=ExtraTreesRegressor, seed=SEED, params=et_params)
rf = SklearnWrapper(clf=RandomForestRegressor, seed=SEED, params=rf_params)
rd = SklearnWrapper(clf=Ridge, seed=SEED, params=rd_params)
ls = SklearnWrapper(clf=Lasso, seed=SEED, params=ls_params)
xg_oof_train, xg_oof_test = get_oof(xg)
et_oof_train, et_oof_test = get_oof(et)
rf_oof_train, rf_oof_test = get_oof(rf)
rd_oof_train, rd_oof_test = get_oof(rd)
ls_oof_train, ls_oof_test = get_oof(ls)
print("XG-CV: {}".format(sqrt(mean_squared_error(y_train, xg_oof_train))))
print("ET-CV: {}".format(sqrt(mean_squared_error(y_train, et_oof_train))))
print("RF-CV: {}".format(sqrt(mean_squared_error(y_train, rf_oof_train))))
print("RD-CV: {}".format(sqrt(mean_squared_error(y_train, rd_oof_train))))
print("LS-CV: {}".format(sqrt(mean_squared_error(y_train, ls_oof_train))))
x_train = np.concatenate((xg_oof_train, et_oof_train, rf_oof_train, rd_oof_train, ls_oof_train), axis=1)
x_test = np.concatenate((xg_oof_test, et_oof_test, rf_oof_test, rd_oof_test, ls_oof_test), axis=1)
print("{},{}".format(x_train.shape, x_test.shape))
dtrain = xgb.DMatrix(x_train, label=y_train)
dtest = xgb.DMatrix(x_test)
xgb_params = {
'seed': 0,
'colsample_bytree': 0.8,
'silent': 1,
'subsample': 0.6,
'learning_rate': 0.01,
'objective': 'reg:linear',
'max_depth': 1,
'num_parallel_tree': 1,
'min_child_weight': 1,
'eval_metric': 'rmse',
}
res = xgb.cv(xgb_params, dtrain, num_boost_round=1000, nfold=4, seed=SEED, stratified=False,
early_stopping_rounds=25, verbose_eval=10, show_stdv=True)
best_nrounds = res.shape[0] - 1
cv_mean = res.iloc[-1, 0]
cv_std = res.iloc[-1, 1]
print('Ensemble-CV: {0}+{1}'.format(cv_mean, cv_std))
gbdt = xgb.train(xgb_params, dtrain, best_nrounds)
submission = pd.read_csv(SUBMISSION_FILE)
submission.iloc[:, 1] = gbdt.predict(dtest)
saleprice = np.exp(submission['SalePrice'])-1
submission['SalePrice'] = saleprice
submission.to_csv('xgstacker_starter.sub.csv', index=None)主要参考的kaggle比赛的