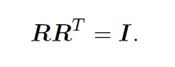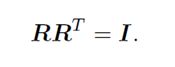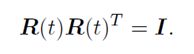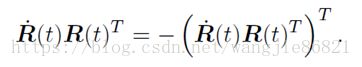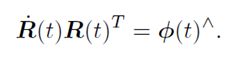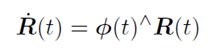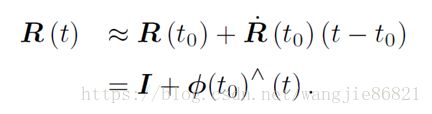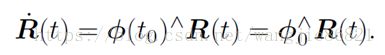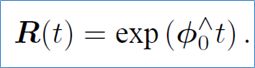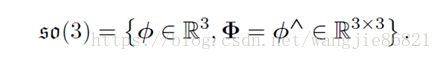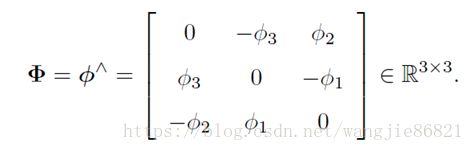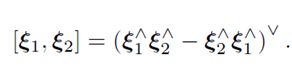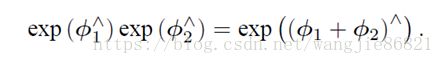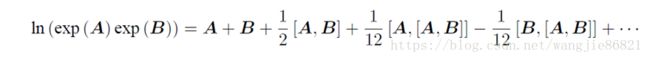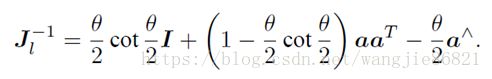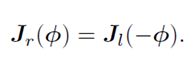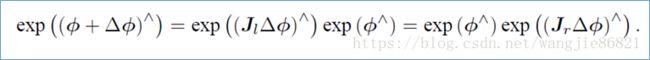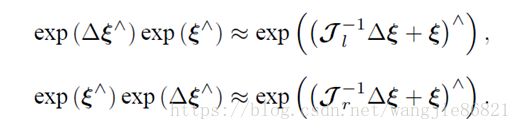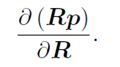SLAM基础之李群和李代数
在做SLAM研究的时候,会涉及到对旋转矩阵求导的问题。然而矩阵求导中多个变换矩阵相加问题很难解决,这时候需要使用矩阵李群的知识,将旋转或者变换等矩阵李群形式,映射到李代数上求解。
李群和李代数
群的概念:群(Group)是一种集合加上一种运算的代数结构。
记集合为A,运算为 · ,那么当运算满足以下性质时,称 (A, · )成群:
我们可以根据群的概念验证得到:
(1)旋转矩阵集合与矩阵乘法构成群
(2)变换矩阵集合与矩阵乘法构成群
在SLAM当中,我们常用到的群一般有特殊正交群和特殊欧氏群两种
李群
李群主要是指:
具有连续(光滑)性质的群。既是群也是流形。
直观上看,一个刚体能够连续地在空间中运动,故SO(3)和SE(3)都是李群。
但是,SO(3)和SE(3)只有定义良好的乘法,没有加法,所以难以进行取极限、求导等操作。所以我们引出了李代数的概念。
李代数
李代数:与李群对应的一种结构,位于向量空间。事实上是李群单位元处的正切空间。
我们通过旋转矩阵来引出李代数,考虑任意旋转矩阵R,满足
令R随时间变化(连续运动),有:
两侧对时间求导,可得:
整理可得:
可以看出,这是一个反对称矩阵,记为:
两侧右乘R(t):
可以认为,对R求导后,左侧多出一个∅(t)
可见∅反映了一阶导数性质,它位于正切空间(tangent space)上,在t0附近,假设∅不变,有微分方程:
已知初始情况:R(0)=I ,解之,得:
上式说明,对任意t,都可以找到一个R和一个的∅对应关系,该关系称为指数映射。
在这里这个∅称为SO(3)对应的李代数:so(3)
现在,我们来定义一下李代数:
其中二元运算[,]被称为李括号,直观上说,李括号表达了两个元素的差异。
对于每个李群,都有与之对应的李代数,李代数描述了李群单位元附件的正切空间性质。
那么对于李代数so(3),我们可以定义
李括号内的运算为:
同理可得,SE(3)亦有李代数se(3)
指数映射和对数映射
指数映射反映了从李代数到李群的对应关系
但是ϕ^是一个矩阵,对于矩阵,如何定义求指数运算?
由于ϕ^是向量,定义其角度和模长可得:
然后对exp(ϕ^)泰勒展开可得:
整理:
而在旋转矩阵中罗德里格斯公式即这个公式,所以,我们可以认为so(3) 的物理意义就是旋转向量。
反之,给定旋转矩阵时,亦能求李代数:
称为对数映射
但实际当中没必要这样求,矩阵到向量的转换关系可以由矩阵的迹得到
在此我们已经得出了李群和李代数的对应关系,下面总结一下在SO(3)和SE(3)中的对应关系。
李代数求导与扰动模型
我们了解到李群跟李代数的对应关系之后,我们回到最初的问题中来,当初就是考虑到旋转矩阵没有加法,所以我们无法定义导数,那么,现在我们该怎么定义导数模型呢?
我们假想,当在李代数中做加法时,是否等价于在李群上做乘法呢? 即:
在使用标量的时候,该式明显成立,然而这儿ϕ^是个矩阵,我们可以使用BCH公式近似:
其中方括号为李括号。
可以得到,当其中一个量为小量时,忽略其高阶项,BCH具有线性近似形式
这里有左雅克比为
右雅克比为:
所以,以左乘为例,即在李群上左乘小量时,李代数上的加法相差左雅可比的逆
同样,李代数上进行小量加法时,相当于李群上左(右)乘一个带左(右)雅可比的量
SE(3)比SO(3)更复杂:
因为在使用过程中用到的不多,所以暂时不展开讨论。
综上:通过BCH线性近似,可以定义李代数上的导数,旋转后的点关于旋转的导数可以不严谨地记为:
由于R没有加法,导数无从定义,所以存在两种解决办法:
1.对 R 对应的李代数加上小量,求相对于小量的变化率(导数模型);
2.对 R 左乘或右乘一个小量,求相对于小量的李代数的变化率(扰动模型)。
对于导数模型,有:
由于雅克比矩阵比较不好运算,考虑扰动模型,
本文主要参考高翔博士的视觉SLAM十四讲以及他在深蓝学院的讲课讲义