【真实原创,转载务必注明出处】
上一个连载中我们已经了解了神经元模型和其工作方式。单个神经元就可以构成一个最简单的神经网络——感知机。在单层神经元感知机中,网络接收若干过输入,并通过输入函数、传输函数给出一个网络的输出。这个网络已经可以解决苹果和香蕉的分类问题。在本系列中,将具体介绍其内部原理。
首先,我们确定感知机的输入。在此,我们引入形状和颜色两个变量,苹果的形状为圆形记为1,颜色为红色记为1;香蕉的形状为弯形记为-1,颜色为黄色记为-1。则有输入p如表3.1所示。
表3.1 常用传输函数列表
| P |
形状 |
颜色 |
| 苹果 |
1 |
1 |
| 香蕉 |
-1 |
-1 |
其次可以确定传输函数f为Step函数。由于Step函数只能有1和0两种输出,故在此处,定义输出1表示苹果,输出0表示香蕉。
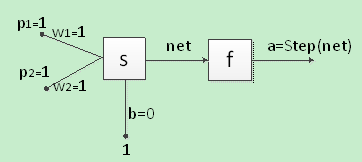
令权重w1=1,w2=1,b=0,则有图3.1所示的感知机,它有两个输入,并且都是1。这表示圆形,并且红色。
此时,net=p1*w1+p2*w2+b
=1+1+0
=2
Step(net)=1
可以看到当输入苹果属性时,感知机正确输出了1,表示苹果。
同样道理当输入-1、-1的香蕉属性时,感知机反应如下:
net=p1*w1+p2*w2+b
=-1-1+0
=-2
Step(net)=0
感知机又作出了正确的判断,当遇到弯的黄色水果时,感知机判断其为香蕉。
虽然感知机在此时已经可以做出来正确的判断,但是我相信读者一定会觉得很疑惑,权值w1、w2和b究竟为什么定义为1、1、0?如果取其它值,感知机还可以正常工作吗?应该如何求出权重和偏置的取值呢?
首先,必须知道,权重和偏置的取值会直接关系到感知机能否正常工作,并不是所有的取值都可以使感知机正常工作。但所幸的是,即使弄错了权值和偏置,还可以使用一套感知机的学习规则,通过不断的迭代学习,求得可以使感知机正常工作的权值和偏置。
感知机学习规则如下:
wnew=wold+ep
bnew=bold+e
其中e表示误差,e=t-a,t为期望输出,a为实际输出。
此规则的含义是,如果感知机的输出有误,则首先计算误差e,e为期望输出和实际输出的差值。新的权值等于旧值加上误差和输入p的乘积。同理,偏置可以看做是输入p恒为1的输入信号,故新的偏置等于旧偏置加入误差。当计算机出新的权重和偏置后,使用测试数据再次测试感知机,直到没有误差或误差在可接受范围内为止。
设w1=1,w2=-1,b=0,输入苹果属性1,1。得到:
net=p1*w1+p2*w2+b
=1-1+0
=0
Step(net)=0
输出错误,存在误差,故进行修正。
e=t-a
=1-0
=1
w1new=w1old+ep
=1+1*1
=2
w2new=w2old+ep
=-1+1*1
=0
bnew=bold+e
=0+1
=1
使用新的权值带入感知机,重新计算苹果的属性输入。
net=p1*w1+p2*w2+b
=1*2+1*0+1
=3
Step(net)=1
纠正误差后,苹果判断正确。尝试判断香蕉。
net=p1*w1+p2*w2+b
=-1*2-1*0+1
=-1
Step(net)=0
香蕉判断也正确,误差为0,学习结束。由此可见,即使初始权值是错误的,只要按照感知机学习规则修正权值和偏置,在感知机的可判断范围内,就有可能消除误差或将误差限制在可接收范围内。
感知机的基本原理已经基本介绍完毕。下面就可以动手实现自己的感知机了。为了方便读者理解,本书使用Java来实现神经网络,并引入神经网络框架neuroph,辅助神经网络的实现。有关neuroph框架以及感知机的具体实现,将在下一章节做详细介绍。