本文从属于笔者的数据结构与算法系列文章。
BinarySearchTree
图解:二叉搜索树算法(BST)
binary-search-tree-complete-implementation
二叉查找树可以递归地定义如下,二叉查找树或者是空二叉树,或者是满足下列性质的二叉树:
(1)若它的左子树不为空,则其左子树上任意结点的关键字的值都小于根结点关键字的值。
(2)若它的右子树不为空,则其右子树上任意结点的关键字的值都大于根节点关键字的值。
(3)它的左、右子树本身又是一个二叉查找树。
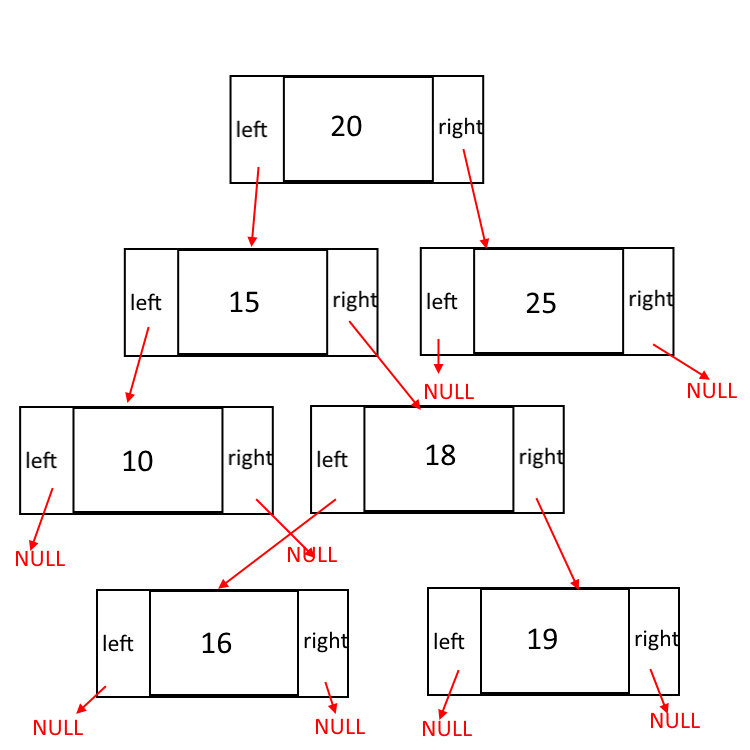
从性能上来说如果二叉查找树的所有非叶子结点的左右子树的结点数目均保持差不多(平衡),那么二叉查找树的搜索性能逼近二分查找;但它比连续内存空间的二分查找的优点是,改变二叉查找树结构(插入与删除结点)不需要移动大段的内存数据,甚至通常是常数开销。二叉查找树可以表示按顺序序列排列的数据集合,因此二叉查找树也被称为二叉排序树,并且同一个数据集合可以表示为不同的二叉查找树。二叉查找树的结点的数据结构定义为:
struct celltype{
records data;
celltype * lchild, * rchild;
}
typedef celltype * BST;
在Java中,节点的数据结构定义如下:
package wx.algorithm.search.bst;
/**
* Created by apple on 16/7/29.
*/
/**
* @function 二叉搜索树中的节点
*/
public class Node {
//存放节点数据
int data;
//指向左子节点
Node left;
//指向右子节点
Node right;
/**
* @function 默认构造函数
* @param data 节点数据
*/
public Node(int data) {
this.data = data;
left = null;
right = null;
}
}
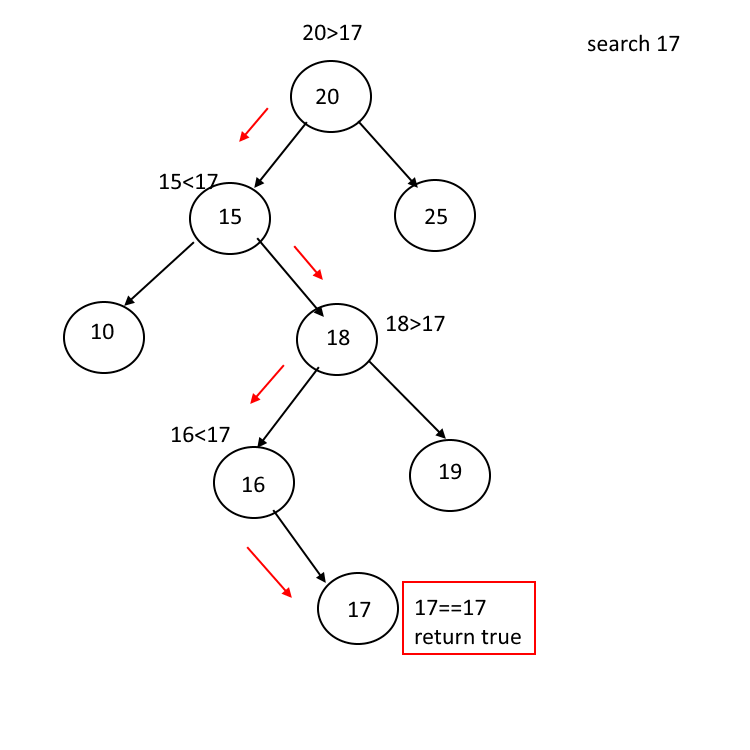
查找
而二叉查找树的查找过程为从根结点开始,如果查询的关键字与结点的关键字相等,那么就命中;否则,如果查询关键字比结点关键字小,就进入左儿子;如果比结点关键字大,就进入右儿子;如果左儿子或右儿子的指针为空,则报告找不到相应的关键字。
BST Search(keytype k, BST F){
//在F所指的二叉查找树中查找关键字为k的记录。若成功,则返回响应结点的指针,否则返回空
if(F == NULL) //查找失败
return NULL;
else if(k == F -> data.key){ //查找成功
return F;
}
else if (k < F -> data.key){ //查找左子树
return Search(k,F -> lchild);
}
else if (k > F -> data.key){ //查找右子树
return Search(k,F -> rchild);
}
}
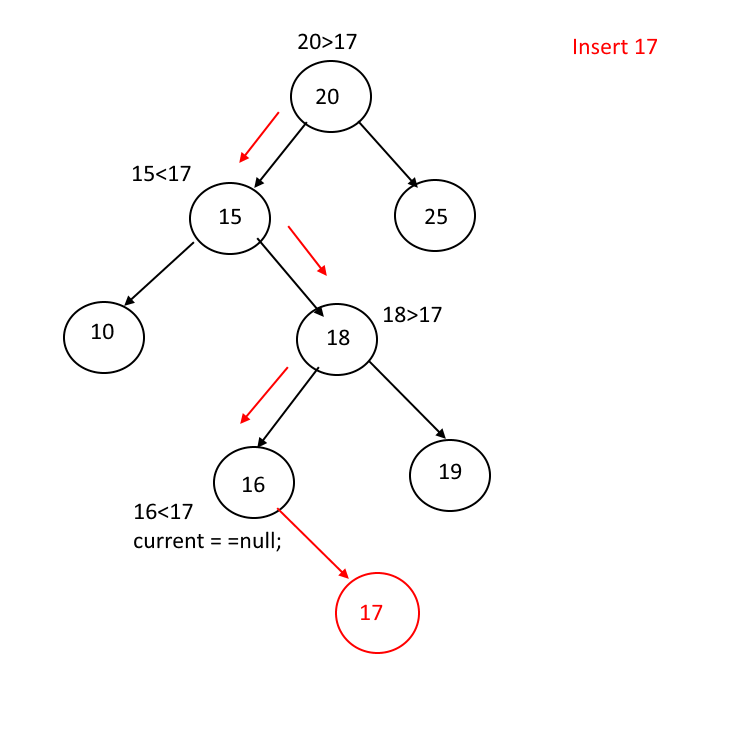
插入
把一个新的记录R插入到二叉查找树,应该保证在插入之后不破坏二叉查找树的结构性质。因此,为了执行插入操作首先应该查找R所在的位置。查找时,仍然采用上述的递归算法。若查找失败,则把包含R的结点插在具有空子树位置,若查找成功,则不执行插入,操作结束。
void Insert(records R, BST &F){
//在F所指的二叉查找树中插入一个新纪录R
if(F == NULL){
F = new celltype;
F -> data = R;
F -> lchild = NULL;
F -> rchild = NULL;
}
else if (R.key < F -> data.key){
Insert(R,F -> lchild);
}else if(R.key > F -> data.key){
Insert(R,F -> rchild);
}
//如果 R.key == F -> data.key 则返回
}
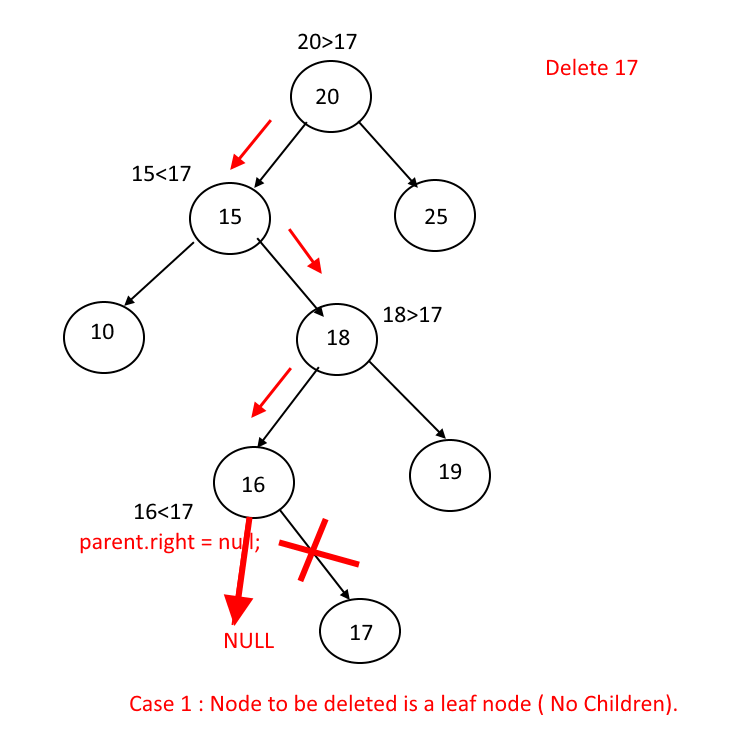
删除
删除叶节点
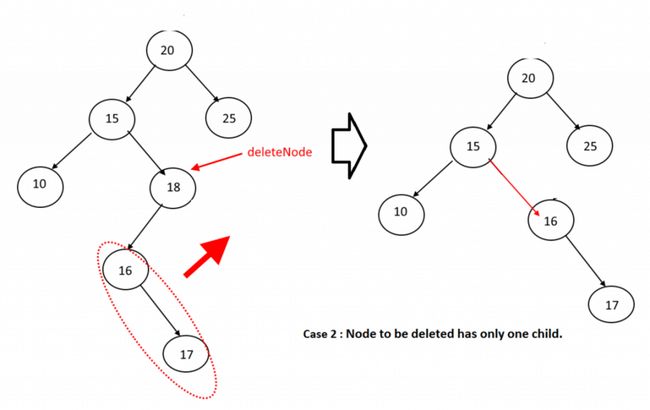
删除只有一个子节点的内部节点
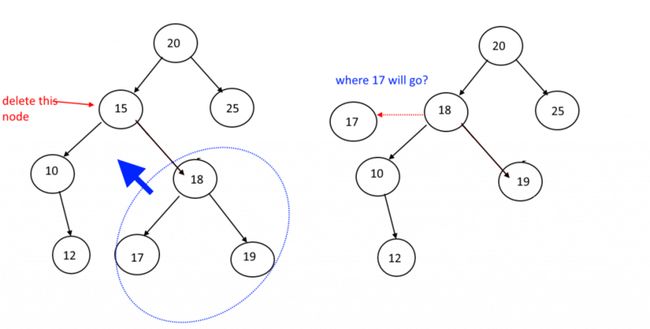
删除有两个子节点的内部节点
如果我们进行简单的替换,那么可能碰到如下情况:
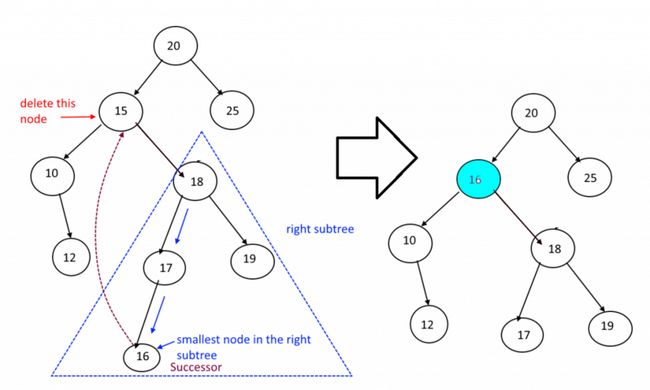
因此我们要在子树中选择一个合适的替换节点,替换节点一般来说会是右子树中的最小的节点:
Java Implementation
BinarySearchTree的Java版本代码参考BinarySearchTree:
package wx.algorithm.search.bst;
/**
* Created by apple on 16/7/29.
*/
/**
* @function 二叉搜索树的示范代码
*/
public class BinarySearchTree {
//指向二叉搜索树的根节点
private Node root;
//默认构造函数
public BinarySearchTree() {
this.root = null;
}
/**
* @param id 待查找的值
* @return
* @function 默认搜索函数
*/
public boolean find(int id) {
//从根节点开始查询
Node current = root;
//当节点不为空
while (current != null) {
//是否已经查询到
if (current.data == id) {
return true;
} else if (current.data > id) {
//查询左子树
current = current.left;
} else {
//查询右子树
current = current.right;
}
}
return false;
}
/**
* @param id
* @function 插入某个节点
*/
public void insert(int id) {
//创建一个新的节点
Node newNode = new Node(id);
//判断根节点是否为空
if (root == null) {
root = newNode;
return;
}
//设置current指针指向当前根节点
Node current = root;
//设置父节点为空
Node parent = null;
//遍历直到找到第一个插入点
while (true) {
//先将父节点设置为当前节点
parent = current;
//如果小于当前节点的值
if (id < current.data) {
//移向左节点
current = current.left;
//如果当前节点不为空,则继续向下一层搜索
if (current == null) {
parent.left = newNode;
return;
}
} else {
//否则移向右节点
current = current.right;
//如果当前节点不为空,则继续向下一层搜索
if (current == null) {
parent.right = newNode;
return;
}
}
}
}
/**
* @param id
* @return
* @function 删除树中的某个元素
*/
public boolean delete(int id) {
Node parent = root;
Node current = root;
//记录被找到的节点是父节点的左子节点还是右子节点
boolean isLeftChild = false;
//循环直到找到目标节点的位置,否则报错
while (current.data != id) {
parent = current;
if (current.data > id) {
isLeftChild = true;
current = current.left;
} else {
isLeftChild = false;
current = current.right;
}
if (current == null) {
return false;
}
}
//如果待删除的节点没有任何子节点
//直接将该节点的原本指向该节点的指针设置为null
if (current.left == null && current.right == null) {
if (current == root) {
root = null;
}
if (isLeftChild == true) {
parent.left = null;
} else {
parent.right = null;
}
}
//如果待删除的节点有一个子节点,且其为左子节点
else if (current.right == null) {
//判断当前节点是否为根节点
if (current == root) {
root = current.left;
} else if (isLeftChild) {
//挂载到父节点的左子树
parent.left = current.left;
} else {
//挂载到父节点的右子树
parent.right = current.left;
}
} else if (current.left == null) {
if (current == root) {
root = current.right;
} else if (isLeftChild) {
parent.left = current.right;
} else {
parent.right = current.right;
}
}
//如果待删除的节点有两个子节点
else if (current.left != null && current.right != null) {
//寻找右子树中的最小值
Node successor = getSuccessor(current);
if (current == root) {
root = successor;
} else if (isLeftChild) {
parent.left = successor;
} else {
parent.right = successor;
}
successor.left = current.left;
}
return true;
}
/**
* @param deleleNode
* @return
* @function 在树种查找最合适的节点
*/
private Node getSuccessor(Node deleleNode) {
Node successsor = null;
Node successsorParent = null;
Node current = deleleNode.right;
while (current != null) {
successsorParent = successsor;
successsor = current;
current = current.left;
}
if (successsor != deleleNode.right) {
successsorParent.left = successsor.right;
successsor.right = deleleNode.right;
}
return successsor;
}
/**
* @function 以中根顺序遍历树
*/
public void display() {
display(root);
}
private void display(Node node) {
//判断当前节点是否为空
if (node != null) {
//首先展示左子树
display(node.left);
//然后展示当前根节点的值
System.out.print(" " + node.data);
//最后展示右子树的值
display(node.right);
}
}
}测试函数:
package wx.algorithm.search.bst;
import org.junit.Before;
import org.junit.Test;
/**
* Created by apple on 16/7/30.
*/
public class BinarySearchTreeTest {
BinarySearchTree binarySearchTree;
@Before
public void setUp() {
binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(3);
binarySearchTree.insert(8);
binarySearchTree.insert(1);
binarySearchTree.insert(4);
binarySearchTree.insert(6);
binarySearchTree.insert(2);
binarySearchTree.insert(10);
binarySearchTree.insert(9);
binarySearchTree.insert(20);
binarySearchTree.insert(25);
binarySearchTree.insert(15);
binarySearchTree.insert(16);
System.out.println("原始的树 : ");
binarySearchTree.display();
System.out.println("");
}
@Test
public void testFind() {
System.out.println("判断4是否存在树中 : " + binarySearchTree.find(4));
}
@Test
public void testInsert() {
}
@Test
public void testDelete() {
System.out.println("删除值为2的节点 : " + binarySearchTree.delete(2));
binarySearchTree.display();
System.out.println("\n 删除有一个子节点值为4的节点 : " + binarySearchTree.delete(4));
binarySearchTree.display();
System.out.println("\n 删除有两个子节点的值为10的节点 : " + binarySearchTree.delete(10));
binarySearchTree.display();
}
}![]()