K-Nearest Neighbor理解笔记（KNN原理及代码实现）

目录

邻近算法(Nearest Neighbor)

概念原理

算法分析

代码实现

K近邻算法（K-Nearest Neighbor）

概念原理

算法分析

代码实现

优缺点分析：

 

---

 

邻近算法(Nearest Neighbor)

 

概念原理

        邻近算法(Nearest Neighbor)的思想实际上十分简单，就是将测试图片和储存起来的训练集一一进行相似度计算，计算出最相近的图片，这张图片的标签便是赋给测试图片的分类标签。

那么如何比较两组数据之间的相似长度呢？

 

算法分析

        最常用的两种方式： ①L1距离(Manhattan distance)

                                         ②L2距离(Euclidean  distance)

 

一、Manhattan distance

计算公式：

                                  

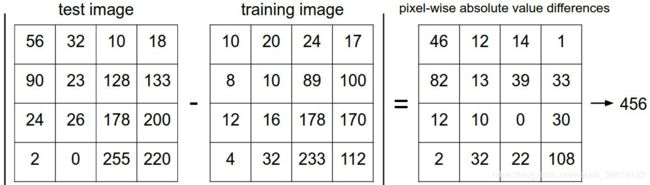
在图片上的具体反映：

在上述图片中最右侧的数字就是distance

两张图片使用L1距离来进行比较。逐个像素求差值，然后将所有差值加起来得到一个数值。如果两张图片一模一样，那么L1距离为0，但是如果两张图片很是不同，那L1值将会非常大。

 

代码实现：

#coding: utf-8
import numpy as np
import cv2 as cv
import _pickle as pickle

def load_CIFAR10(filename):
    """载入cifar数据集的一个batch"""
    training_file = filename + "/data_batch_1"
    testing_file = filename + "/test_batch"

    #载入训练集
    with open(training_file, 'rb') as f:
        data = pickle.load(f, encoding='iso-8859-1')
        Xtr = data['data']
        Xtr = Xtr[:300]   #由于一个batch中有10000张图片，碍于计算速度，这里只载入300张图片
        Ytr = data['labels']
        Ytr = Ytr[:300]


    #载入测试集
    with open(testing_file, 'rb') as f:
        data = pickle.load(f, encoding='iso-8859-1')
        Xte = data['data']
        Xte = Xte[:300]    #同上诉处理
        Yte = data['labels']
        Yte = Yte[:300]

    return Xtr, Ytr, Xte, Yte  #返回数据


#邻近算法
class NearestNeighbor(object):
    def __init__(self):
        pass

    def train(self, X, Y):
        self.Xtr = X
        self.Ytr = Y

    #计算Manhattan距离
    def predict_L1(self, X):
        num_test = X.shape[0]
        Ypred = np.zeros(num_test)

        #计算训练集和测试集之间的距离
        for i in range(num_test):
            #print("i:  " ,i)
            distances = np.sum(np.abs(self.Xtr - X[i, :]), axis=1)
            min_index = np.argmin(distances)
            Ypred[i] = self.Ytr[min_index]
        return Ypred

    #计算Euclidean距离
    def predict_L2(self, X):
        num_test = X.shape[0]
        Ypred = np.zeros(num_test)

        for i in range(num_test):
            #print("i:  " ,i)
            distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))
            min_index = np.argmin(distances)
            Ypred[i] = self.Ytr[min_index]
        return Ypred


Xtr, Ytr, Xte, Yte = load_CIFAR10("./data/cifar-10")

#进行Nearest Neighbor运算
nn = NearestNeighbor()
nn.train(Xtr, Ytr)
Yte_predict = nn.predict_L2(Xte)
print(Yte_predict)
print('accuracy: %f' % (np.mean(Yte_predict == Yte)))

 

K近邻算法（K-Nearest Neighbor）

 

概念原理

        在邻近算法(Nearest Neighbor)的思想中，我们只计算最相近的图片的标签。但是，在实际上，为了更好的效果，我们可以找最相似的K张图片，然后用这K张图片中数量最多的标签作为测试图片的分类标签。

 

算法分析

        最常用的两种方式： ①L1距离(Manhattan distance)

                                         ②L2距离(Euclidean  distance)                  ----其实么得变化

只是将一张图片扩增为K张图片。

 

代码实现：

#coding: utf-8
import numpy as np
import cv2 as cv
import _pickle as pickle
import heapq

def load_CIFAR10(filename):
    """载入cifar数据集的一个batch"""
    training_file = filename + "/data_batch_1"
    testing_file = filename + "/test_batch"
    #载入训练集
    with open(training_file, 'rb') as f:
        data = pickle.load(f, encoding='iso-8859-1')
        Xtr = data['data']
        Xtr = Xtr[:300]
        Ytr = data['labels']
        Ytr = Ytr[:300]
  #  print("len:", len(Xtr[0]))
    #载入测试集
    with open(testing_file, 'rb') as f:
        data = pickle.load(f, encoding='iso-8859-1')
        Xte = data['data']
        Xte = Xte[:300]
        Yte = data['labels']
        Yte = Yte[:300]

    return Xtr, Ytr, Xte[0], Yte[0]


class NearestNeighbor(object):
    def __init__(self):
        pass

    def train(self, X, Y):
        self.Xtr = X
        self.Ytr = Y

    def predict_L1(self, X):
        num_test = X.shape[0]
        Ypred = np.zeros(num_test)

        img_distance = []
        for i in range(num_test):
            # print("i:  " ,i)
            distance = np.sum(np.abs(self.Xtr[i] - X))
            img_distance.append(distance)
        #取出前K个最小的值
        min_dist = map(img_distance.index, heapq.nsmallest(K, img_distance))
        for i in list(min_dist):
            Ypred[i] = Ytr[i]

        print("Ypred: ", Ypred)
        label_count = []
        for i in range(0, 9):
            label_count.append(list(Ypred).count(i))
        label = np.argmax(label_count)
        return label

    def predict_L2(self, X, K):
        num_test = self.Xtr.shape[0]
        Ypred = np.zeros(num_test)

        img_distance = []
        for i in range(num_test):

            #print("i:  " ,i)
            distance = np.sqrt(np.sum(np.square(self.Xtr[i] - X)))
            img_distance.append(distance)
        #取出前K个最小的值
        min_dist = map(img_distance.index, heapq.nsmallest(K, img_distance))
        for i in list(min_dist):
            Ypred[i] =Ytr[i]

        print("Ypred: ",Ypred)
        label_count = []
        for i in range(0,9):
            label_count.append(list(Ypred).count(i))
        label = np.argmax(label_count)
        return label


Xtr, Ytr, Xte, Yte = load_CIFAR10("./data/cifar-10")
#Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3)
#Xte_rows = Xte.reshape(Xtr.shape[0], 32 * 32 * 3)
#print("Xte_rows：", Xte_rows)
nn = NearestNeighbor()
nn.train(Xtr, Ytr)
Yte_predict = nn.predict_L2(Xte,5)
print("Xtr: ", Xtr.shape)
print(Yte_predict)
print('accuracy: %f' % (np.mean(Yte_predict == Yte)))

那么在K-NN中，K的值应该如何选出呢?

在这里，需要指出的是，K-NN的K值与我们所选择的计算图像距离的方式L1或者L2一样，我们尚且思考，在计算距离时，我们到底是应该选择L1还是L2呢？当你发出这样的提问时，你就会发现，这就如同思考，K的取值一般。K可以是2、3、4，那为什么不能是5、6、7呢？所以，这实际上，是以最后的结果好坏为导向性的。这一类在training中无法learn到，需要人为设置的参数，称之为超参数（hyperparameter），与参数不同，参数是在整个训练过程中可以不断优化得到最终结果的，超参数只能一开始就认为设置。

那么怎么才能确定自己选择的超参数是好的呢？

一遍遍的不断尝试，通过结果好坏进行分析。（要不怎么说人工智能，首先要有人工才能有智能呢，小声bb.....）

 

优缺点分析：

 

缺点：

其实基本上，在图像识别上，是基本不会用到KNN的，因为KNN的最终结果很大程度上是以背景为导向的。

举一个栗子：

这时一只草地上的小狗：                                                   这时一只在沙发上的小猫：

                        

 

那么，当我们有一只在草地上的猫咪时，会如何呢？

使用KNN的话，基本上，会认为是与上面左边的在草地上的狗最相似，因为，两张图片上，有着更多的相似像素点，这样一来，距离也就更加相近。你可以认为是，KNN记住了绿色的背景。所以说，他是以背景为导向的。

还有就是，由于KNN的计算特殊性，在所谓的训练阶段，KNN只是简单的储存所有的训练集，然后在检测阶段，进行一一的对比。这样就造成一个问题，那就是在检测阶段花费时间太长，使得基本不可能商用（也就是约等于没用233）。

优点：

但是其实，优点还是有的，因为使用了KNN总比你瞎猜强。

 

好啦，以上就真的是KNN的所有内容啦，感谢各位看官。