位图(bitmap)的理解及应用实例 布隆过滤
位图是内存中连续的二进制位,用于大量整型数的查询和去重。
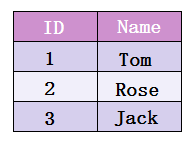
比如,给定10bit的内存空间,要将{5,3,4,7}插入其中。
则,先将第5位置1,
再将3,4,7 依次置1。

这样,此时bitmap中存储了哪些元素,就一目了然。
bitmap还可以用于去掉重复的整型值。
在一个用户表中,一个用户对应多种标签。
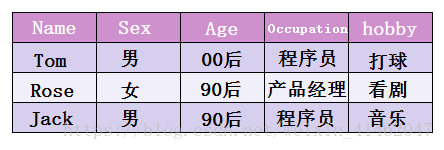
我们可以多个标签对应一个用户。
然后,让每一个标签存储包含此标签的所有的ID,每一个标签都是一个独立的bitmap。

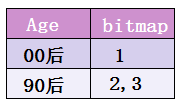
等等…
位图
- 优点:1.节省空间(相比HashSet或HashMap)
2.运算快,交集或并集运算,使用位运算。(比如,要找“90后的程序员”,就用“90后”和”程序员”标签的bitmap取交集) - 缺点:不支持非运算。(如果想要取非,可以定义一个全量用户的bitmap,两者相异或,就可以取非)
位图的实现:
- JDK中BitSet就是对bitmap算法的实现
- 谷歌的EWAHCompressedBitmap是一种更优化的实现
EWAHCompressedBitmap
把bitmap存储在long数组中
这样,对于及其稀疏的bitmap,这种存储方式就会节省大量空间。
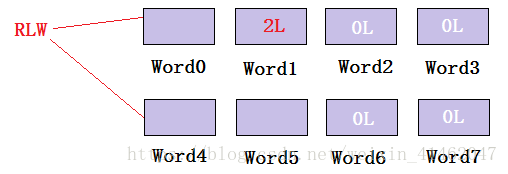
一个新数据的插入,就要依靠每一个RLW作为路标,然后找到自己该插的位置。
这种结构,按照顺序插会比较容易些,如果要插入的数已经被RLW跨过去了的话,就要将RLW拆开,会比较麻烦。官方也建议使用者按照顺序,从小到大的插入。
*Though you can set the bits in any order (e.g., set(100), set(10), set(1),
* you will typically get better performance if you set the bits in increasing order (e.g., set(1), set(10), set(100)).
*
* Setting a bit that is larger than any of the current set bit
* is a constant time operation. Setting a bit that is smaller than an
* already set bit can require time proportional to the compressed
* size of the bitmap, as the bitmap may need to be rewritten.
问题及应用实例
1 使用位图法判断整形数组是否存在重复
判断集合中存在重复是常见编程任务之一,当集合中数据量比较大时我们通常希望少进行几次扫描,这时双重循环法就不可取了。
位图法比较适合于这种情况,它的做法是按照集合中最大元素max创建一个长度为max+1的新数组,然后再次扫描原数组,遇到几就给新数组的第几位置上1,如遇到 5就给新数组的第六个元素置1,这样下次再遇到5想置位时发现新数组的第六个元素已经是1了,这说明这次的数据肯定和以前的数据存在着重复。这种给新数组初始化时置零其后置一的做法类似于位图的处理方法故称位图法。它的运算次数最坏的情况为2N。如果已知数组的最大值即能事先给新数组定长的话效率还能提高一倍。
2 在2.5亿个整数中找出不重复的整数,注,内存不足以容纳这2.5亿个整数
解法一:将bit-map扩展一下,采用2-Bitmap(每个数分配2bit,00表示不存在,01表示出现一次,10表示多次,11无意义)进行,共需内存2^32 * 2 bit=1 GB内存,还可以接受。然后扫描这2.5亿个整数,查看Bitmap中相对应位,如果是00变01,01变10,10保持不变。所描完事后,查看bitmap,把对应位是01的整数输出即可。
或者我们不用2bit来进行表示,我们用两个bit-map即可模拟实现这个2bit-map,都是一样的道理。
解法二:也可采用与第1题类似的方法,进行划分小文件的方法。然后在小文件中找出不重复的整数,并排序。然后再进行归并,注意去除重复的元素。
2.1 一个序列里除了一个元素,其他元素都会重复出现3次,设计一个时间复杂度与空间复杂度最低的算法,找出这个不重复的元素。
3 已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数。
8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。 (可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit==1.2MBytes,这样,就用了小小的1.2M左右的内存表示了所有的8位数的电话)
4 给40亿个不重复的unsigned int的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那40亿个数当中?
解析:bitmap算法就好办多了。申请512M的内存,一个bit位代表一个unsigned int值,读入40亿个数,设置相应的bit位;读入要查询的数,查看相应bit位是否为1,为1表示存在,为0表示不存在。
Note: unsigned int最大数为2^32 - 1,所以需要2^32 - 1个位,也就是(2^32 - 1) / 8 /10 ^ 9G = 0.5G内存。
逆向思维优化:usinged int只有接近43亿(unsigned int最大值为232-1=4294967295,最大不超过43亿),所以可以用某种方式存没有出现过的3亿个数(使用数组{大小为3亿中最大的数/8 bytes}存储),如果出现在3亿个数里面,说明不在40亿里面。3亿个数存储空间一般小于40亿个。(xx存储4294967296需要512MB, 存储294967296只需要35.16MBxx)
5 给定一个数组a,求所有和为SUM的两个数。
如果数组都是整数(负数也可以,将所有数据加上最小的负数x,SUM += 2x就可以了)。如a = [1,2,3,4,7,8],先求a的补数组[8,7,6,5,2,1],开辟两个数组b1,b2(最大数组长度为SUM/8/2{因为两数满足和为SUM,一个数 < SUM / 2,另一个数也就知道了},这样每个b数组最大内存为SUM/(8*2*1024*1024) = 128M),使用bitmap算法和数组a分别设置b1b2对应的位为1,b1b2相与就可以得到和为SUM的两个数其中一个数了。
布隆过滤
以bitmap为基础的排重算法。
应用:URL的排重;垃圾邮箱地址的过滤
- 创建bitmap集合
- 把第一个URL按照三种不同的Hash算法,生成三种不同的Hash值。
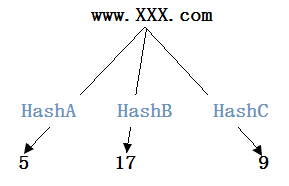
- 分别判断5,17,9对应的位置是否为1,只要不同时为1,就认为该URL没有重复,然后把5,17,9对应位置置1。
当被置1的位变多了,有可能没有重复的URL,Hash出来的结果,对应的位数都是1,那么就误判了。为减小误判的几率,可以让bitmap的空间更大一些,单个URL所做的Hash更多(一般是8次)。
垃圾邮箱的过滤,则可以考虑加上白名单。
:-)