吴恩达机器学习(三)（logistics回归）

分类问题：先从一个二元分类开始。二元分类问题是让我去将问题分成两类，这两类互相呈对立面。

logistics回归的本质上就是研究sigmoid（激活）函数，
y=1/（1+e^-x）也可以叫做logistics函数，他是个生物学概念函数。
我们可以看到激活函数经过（0,0.5），当我们将第一节课学的拟合函数
h_θ(x)=θ^Tx（θ，x默认是一个列向量）外面再套上一层对应关系g()，这个对应关系就是激活函数中x与y的关系。
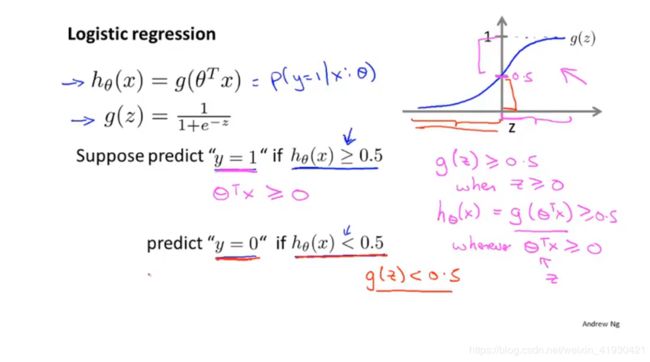
如图，令其θ^Tx=Z为横坐标；当h_θ(x)大于等于0.5时，Z正好对应这大于零，反之亦然。
同时我们在描述这个h_θ(x)=g(θ^Tx)=1/（1+e^-Z）的时候，基于他的最大值为1，和如果过0点，那么其纵坐标值也将大于0.5这个特点，如果假设条件是当输出值h_θ(x)>0.5时我们自动判断一个实际情况y=1，反之y=0。那么他就表示成
P(y=1|x；θ)，他表示在x和θ一定条件下的y=1的概率，在线性回归中h_θ(x)这个原本是拟合曲线的狗东西现在变成了概率了。参数θ和数据的特征量x我们在没有实际情况出现前都是不知道的。当然，如果数据是以0为u的正态分布，那么y=0或者1都将接近百分之五十。

上面我们提到了如果说参数θ和数据的特征量x不确定的情况下，那么判断这个y=0,1是无法进行的。那么现在我们定义了如果给定了θ，如下图θ=[-3 1 1]’;我们就能发现在以特征量x为坐标轴的坐标系上面产生了一条边界。我们称他就是决策边界
从下图我们可以发现，决策边界仅仅与θ有关，而与数据无关，它不代表数据的属性。

我们来看稍微复杂的一个例子，我们给原来的h_θ(x)增加两个特征量x₁²，x₂²
那么问题来了，我们可以随便增加特征量吗？答案自然是可以的，我们可以回顾第一课笔记中的以三角函数为基函数的非线性拟合，这里的基函数就相当于特征的意思，当我们使用在1,x,x² 。。。的时候一样可以进行拟合，特征选择的时候关键是看数据特征和你想要什么样的决策边界。
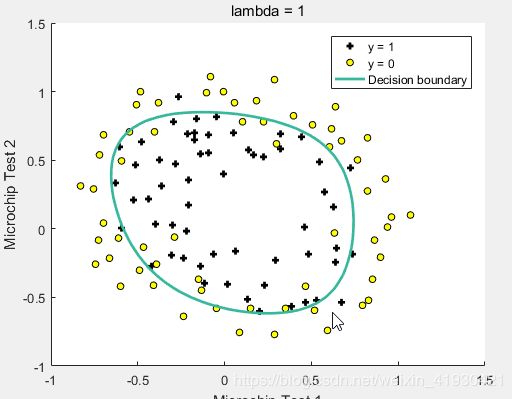
下图的决策边界就是一个圆。

我们现在学习如何去拟合θ，我假定了m组特征，m组y值，这个y值我们称他为标签值，也就是实际情况。二元分类问题中它是非零即一。每一个特征当中有n+1的训练数据。h_θ(x)的对应关系是激活函数。

现在去定义一个代价函数，如果这个代价函数最小，那我们就找到了一个最能体现输出值h_θ(x)表达实际情况y的θ值，也就是能做预测了。

我们将之前学的线性拟合代价函数中1/2m中的1/2放到求和符号的里面，然后去定义这里面为一个cost函数，我们如果把h_θ(x)=g(θ^Tx)=1/（1+e^-Z）这个对应关系放入到cost函数中回代就会发现，J会变成如图一的有多个局部最优解的非凸函数，它不会像梯度下降线性回归中的代价函数一样呈现一个单弓型凸函数（那么最优解就好找了），就是因为他现在用在了logistics回归上。

基于上面的复杂情况，我们重新定义了一个cost函数，他的方程如下，他的概念不再是输出值和y的差值的平方了，而是在原来的sigmoid对应关系上套了一层log的鬼玩意儿。

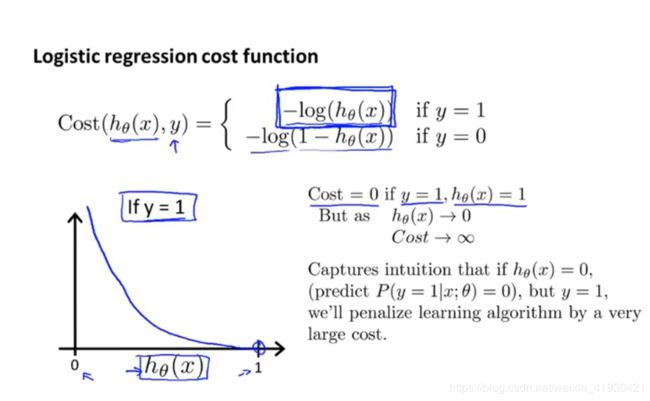
cost函数（有log的）

我们可以看到他的图像是在当实际情况是y=1的时候，输出值h_θ(x)=1，cost函数为0。也就是说，如果我们的这个输出值h_θ(x)=1，实际情况y=1那么cost也就是0了，这个h_θ(x)在取值上就是和y比较相像了，损失比较小了。这比较符合常理。当然如果说实际情况y=0，但是输出值h_θ(x)=1，那么cost就会是无穷大，也就是说如果我预测一个东西，但是这个东西和实际情况是截然相反的。那么我付出的损失将是巨大的。这样也是符合常理。所以也验证了这个log对应关系的科学性。

为了偷懒，我们将上面的cost函数写成紧凑格式如下
cost(h_θ(x),y)=-ylog(h_θ(x))-(1-y)log(1-h_θ(x))
代入原J中

我们在计算梯度的时候，带入h_θ(x)=1/（1+e^-Z）后求偏导，即是下面手写的这行公式

我们现在需要搞清楚的是θ取到何值的时候J会变的最小，J变小也相当于cost函数最小，表明了我们的输出预测概率值h_θ(x)更好的体现实际情况标签量y。那实际上和之前学过的梯度下降是一样的

数据可视化，计算代价函数和梯度

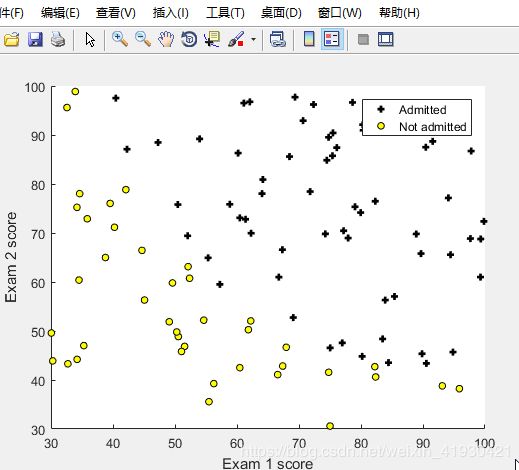
例题一：在本部分练习中，您将建立一个逻辑回归模型，以预测学生是否被大学录取。假设您是大学部门的管理员，并且您要根据每个申请人的入学机会来确定他们的入学机会两次考试的结果。 您有以前申请人的历史数据可以用作逻辑回归的训练集。 每次训练例如，您在两次考试和录取中都有申请人的分数决定。0/1表示有没有录取。
您的任务是建立一个分类模型，以估算申请人的入学概率。基于这两次考试的分数下面看例题1的数据：

主函数

clear ; close all; clc
data = load('ex2data1.txt');
X = data(:, [1, 2]); y = data(:, 3);
plotData(X, y);
hold on;
xlabel('Exam 1 score')；      %坐标轴名
ylabel('Exam 2 score')；
legend('Admitted', 'Not admitted')
hold off;

[m, n] = size(X);
X = [ones(m, 1) X];                     %加第一列
initial_theta = zeros(n + 1, 1);     %初始化的θ
[cost, grad] = costFunction(initial_theta, X, y);   
test_theta = [-24; 0.2; 0.2];              %测试的θ格式，x默认格式是一次方1,x1,x2
[cost, grad] = costFunction(test_theta, X, y);    

返回代价函数和梯度

function [J, grad] = costFunction(theta, X, y)      %返回代价函数和梯度值
m = length(y);
J = 0;
grad = zeros(size(theta));
J = 1/m*(-y'*log(sigmoid(X*theta)) - (1-y)'*(log(1-sigmoid(X*theta))));
grad = 1/m * X'*(sigmoid(X*theta) - y);

激活函数

function g = sigmoid(z)
g = zeros(size(z));
g = 1./(1 + exp(-z));
end

画图函数

function plotData(X, y)
figure;
hold on;
pos = find(y==1);      %分出第三列是1/0的特征
neg = find(y == 0);
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, ...
'MarkerSize', 5);          %默认黑色加号，线宽2
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
'MarkerSize', 5);          %黄色的圆

只不过现在的h_θ(x)有了新的对应关系。

这里将介绍优化函数fminunc，这是matlab自带的库函数。他可以帮助你找到第二个向量参数initialtheta的最优解，只需要你将

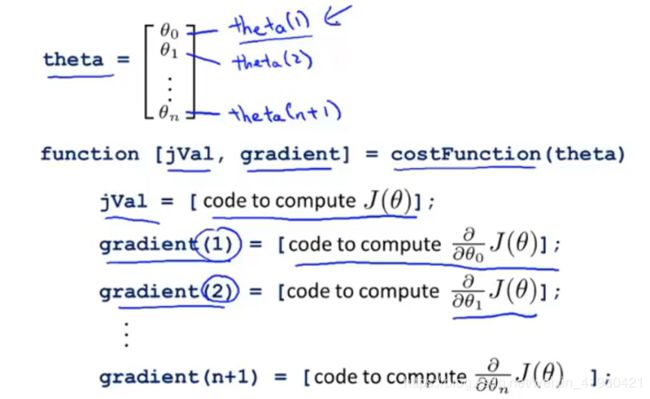
画出决策边界

利用上面的的fminunc函数
你要使用它只需要设置一些参数，option中‘GradObj’表示选择梯度，'on’表示开启，还有最大的迭代次数。
区别于octave，matlab在设置句柄时使用固定格式，@(参数)function（参数1，参数2，，，）

主函数（接上面的主函数）

options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, cost] = ...
	fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);  %自动帅选出合适的initi_theta
	plotDecisionBoundary(theta, X, y);                     %画出决策边界
	hold on;   
	xlabel('Exam 1 score')；
    ylabel('Exam 2 score')； 
legend('Admitted', 'Not admitted')
hold off;

画图函数

function plotDecisionBoundary(theta, X, y)
plotData(X(:,2:3), y);       %输出data前两列
hold on；
if size(X, 2) <= 3             %X数据的列数小于等于三
plot_x = [min(X(:,2))-2,  max(X(:,2))+2];
plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));
plot(plot_x, plot_y)；
          legend('Admitted', 'Not admitted', 'Decision Boundary')；
    axis([30, 100, 30, 100])；
% else
    u = linspace(-1, 1.5, 50);             %建立-1到1.5的50个空间
    v = linspace(-1, 1.5, 50);

    z = zeros(length(u), length(v));
        for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z';
        contour(u, v, z, [0, 0], 'LineWidth', 2)
% end                              
%%  本例可以发现X的列数正好是3，故这一块用不到。
hold off
end

我们去预测一个学生的录取概率
这是后我们已经得到了theta，只需将题目的X带入，并且计算这个预测的准确率是多少？

prob = sigmoid([1 45 85] * theta);
fprintf(['For a student with scores 45 and 85, we predict an admission ' ...
         'probability of %f\n'], prob); %如果一个学生成绩是45 85那么他的概率？
        p = predict(theta, X);
        fprintf('Train Accuracy: %f\n', mean(double(p == y))

可见


octave软件从操作如下：

敲回车之后，鼠标处是因为前面因为前面被遮挡了

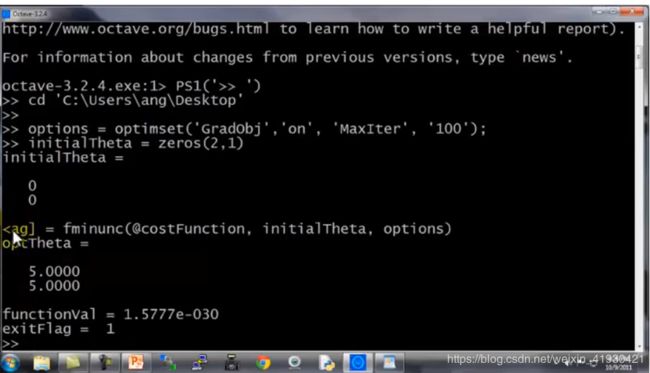
正则化

欠拟合和过拟合，对于泛化数据来说都是不好的。
所以接下来会用到正则化消除一些不需要的特征种类


去减少一些特征量x，正则化：减少θ值

线性回归正则化

加入了正则项（紫色部分）
我们只对θ1开始之后的θ做正则化。

增加惩罚θ₄θ₅的效果
注意下面的式子中惩罚的θ是从1开始的。但是h_θ(x)中是有θ₀的。

最终的代价函数公式为（正则化后）

我们将θ₀分离出来。

最终的θ公式为

简便起见我们不会太考虑学习率α，就假设是1了。
我们将θ₀的迭代式子分离出来，这样比较清晰明了。

当我们使用正规方程做线性回归一步到位时候，θ的计算方法有了如下的变化。

logistic回归的正则化

其中的梯度和代价函数，写的好看点

J = 1/m * (-y' * log(sigmoid(X*theta)) - (1 - y') * log(1 - sigmoid(X * theta))) + lambda/2/m*sum(theta(2:end).^2);

上面式子中2改为n。

grad(1,:) = 1/m * (X(:, 1)' * (sigmoid(X*theta) - y));
grad(2:size(theta), :) = 1/m * (X(:, 2:size(theta))' * (sigmoid(X*theta) - y))... 
        + lambda/m*theta(2:size(theta), :);

例题2

在本部分练习中，您将实现正则逻辑回归预测制造工厂的微芯片是否通过质量保证。在质量检查过程中，每个微芯片都要经过各种测试以确保它运行正常。
假设您是工厂的产品经理，并且您拥有一些微芯片在两种不同测试中的测试结果。 通过这两个测试，您想确定是否应接受微芯片或拒绝。为了帮助您做出决定，您拥有测试结果的数据集在过去（1/0是否合格）的微芯片上，您可以从中构建逻辑回归模型。

主函数

%% 画图函数
data = load('ex2data2.txt');
X = data(:, [1, 2]);
y = data(:, 3);          
plotData(X, y); 
hold on;

xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
legend('y = 1', 'y = 0')
hold off;

%% 计算梯度和theta
X = mapFeature(X(:,1), X(:,2));       %特征提取，X二维扩展到28维度
initial_theta = zeros(size(X, 2), 1);  %初始化theta
lambda = 1;                                     %就是那个λ

[cost, grad] = costFunctionReg(initial_theta, X, y, lambda);       %利用正则化来计算代价函数和梯度
fprintf('Cost at initial theta (zeros): %f\n', cost);               %初始状态下theta所带来的损耗
fprintf(' %f \n', grad(1:5));

%% 正则化回归出拟合曲线和预测准确率
initial_theta = zeros(size(X, 2), 1);
lambda = 1;
options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, J, exit_flag] = fminunc(@(t)(costFunctionReg(t, X, y, lambda)), ...
      initial_theta, options); %仍然是利用fminunc函数来找到最佳的initial_theta
plotDecisionBoundary(theta, X, y);
hold on;
title(sprintf('lambda = %g', lambda))；

xlabel('Microchip Test 1')；
ylabel('Microchip Test 2')；

legend('y = 1', 'y = 0', 'Decision boundary')；
hold off;

p = predict(theta, X);

fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100); %与原来的判断标准进行比较求一个百分比准确率
fprintf('Expected accuracy (with lambda = 1): 83.1 (approx)\n');%判断准确率的答案是83.1

数据2

特征提取函数mapFeature.m

function out = mapFeature(X1, X2)
degree = 6;                                         %最高阶次就是六次方
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end
end

从原来的两个特征扩展到1+2+3+。。。7=28个特征种类。

计算代价和梯度函数（防止过拟合使用了正则化）

costFunctionReg.m

function [J, grad] = costFunctionReg(theta, X, y, lambda)
m = length(y); 
grad = zeros(size(theta));
J = 1/m * (-y' * log(sigmoid(X*theta)) - (1 - y') * log(1 - sigmoid(X * theta))) + lambda/2/m*sum(theta(2:end).^2);
grad(1,:) = 1/m * (X(:, 1)' * (sigmoid(X*theta) - y));
grad(2:size(theta), :) = 1/m * (X(:, 2:size(theta))' * (sigmoid(X*theta) - y))... 
        + lambda/m*theta(2:size(theta), :);
end

预测函数predict.m（还是要用到的）

预测的概率就是sigmoid函数，h_θ(x)。

function p = predict(theta, X)
m = size(X, 1);       %28
p = zeros(m, 1);     %初始化
p = sigmoid(X * theta)>=0.5;  %如果概率大于0.5则是1返回后是118组0/1