Maxout网络学习

原文地址：http://blog.csdn.net/hjimce/article/details/50414467

Maxout算法流程

1. 算法概述

开始前我们先对maxout networks有一个简单的了解。Maxout是深度学习网络中一层网络，就像池化层、卷积层一样等，我们可以把maxout层看作是网络的激活函数层。

我们假设某一层输入的特征向量为：X=（x1,x2,…,xd），也就是我们输入的 d 个神经元。Maxout隐藏层每个神经元的计算公式如下：

上面的公式就是 maxout 层神经元 i 的计算公式。其中，k就是maxout层所需要的参数了，由我们人为设定大小。就像 dropout 一样，也有自己的参数 p（每个神经元dropout的概率），maxout的参数就是 k。公式中Z的计算公式为：

权重 w 是一个大小为（d,m,k）的三维矩阵，b 是一个大小为（m,k）的二维矩阵，这两个就是我们需要学习的参数。如果设定参数k=1，此时网络就类似于以前我们所学普通的网络。

也可以这么理解，本来传统的MLP算法在第 i 层到第 i+1 层，参数只有一组，现在maxout层在这一层同时训练n组参数，然后选择激活值最大的作为下一层神经元的激活值。

为了简单起见，假设我们网络第i层有2个神经元x1、x2，第i+1层的神经元个数为1个，如下图所示：

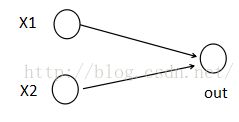
（1) 以前MLP的方法。我们要计算第i+1层，那个神经元的激活值的时候，传统的MLP计算公式就是：

z=W*X+b
out=f(z)
//其中f就是我们所谓的激活函数，比如sigmod，relu，tanh等。

（2）Maxout的方法。如果我们设置maxout的参数k=5，maxout层如下所示：

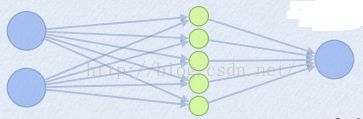
相当于在每个输出神经元前面又多了一层。这一层有5个神经元，此时maxout网络的输出计算公式为：

z1=w1*x+b1

z2=w2*x+b2

z3=w3*x+b3

z4=w4*x+b4

z5=w5*x+b5

out=max(z1,z2,z3,z4,z5)
//所以这就是为什么采用maxout的时候，参数个数成k倍增加的原因。本来我们只需要一组参数就够了，采用maxout后，就需要有k组参数。

2. keras源码

ok，为了学习maxout源码的实现过程，我这边引用keras的源码maxout的实现，进行讲解。keras的网站为：http://keras.io/ 。项目源码网站为：https://github.com/fchollet/keras。下面是keras关于maxout网络层的实现函数：

#maxout 网络层类的定义
class MaxoutDense(Layer):
    # 网络输入数据矩阵大小为(nb_samples, input_dim)
    # 网络输出数据矩阵大小为(nb_samples, output_dim)
    input_ndim = 2
   #nb_feature就是我们前面说的k的个数了，这个是maxout层特有的参数
    def __init__(self, output_dim, nb_feature=4,
                 init='glorot_uniform', weights=None,
                 W_regularizer=None, b_regularizer=None, activity_regularizer=None,
                 W_constraint=None, b_constraint=None, input_dim=None, **kwargs):
        self.output_dim = output_dim
        self.nb_feature = nb_feature
        self.init = initializations.get(init)
 
        self.W_regularizer = regularizers.get(W_regularizer)
        self.b_regularizer = regularizers.get(b_regularizer)
        self.activity_regularizer = regularizers.get(activity_regularizer)
 
        self.W_constraint = constraints.get(W_constraint)
        self.b_constraint = constraints.get(b_constraint)
        self.constraints = [self.W_constraint, self.b_constraint]
 
        self.initial_weights = weights
        self.input_dim = input_dim
        if self.input_dim:
            kwargs['input_shape'] = (self.input_dim,)
        self.input = K.placeholder(ndim=2)
        super(MaxoutDense, self).__init__(**kwargs)
    #参数初始化部分
    def build(self):
        input_dim = self.input_shape[1]
 
        self.W = self.init((self.nb_feature, input_dim, self.output_dim))#nb_feature是我们上面说的k。
        self.b = K.zeros((self.nb_feature, self.output_dim))
 
        self.params = [self.W, self.b]
        self.regularizers = []
 
        if self.W_regularizer:
            self.W_regularizer.set_param(self.W)
            self.regularizers.append(self.W_regularizer)
 
        if self.b_regularizer:
            self.b_regularizer.set_param(self.b)
            self.regularizers.append(self.b_regularizer)
 
        if self.activity_regularizer:
            self.activity_regularizer.set_layer(self)
            self.regularizers.append(self.activity_regularizer)
 
        if self.initial_weights is not None:
            self.set_weights(self.initial_weights)
            del self.initial_weights
 
    def get_output(self, train=False):
        X = self.get_input(train)#需要切记这个x的大小是(nsamples,input_num) 
        # -- don't need activation since it's just linear.
        output = K.max(K.dot(X, self.W) + self.b, axis=1)#maxout激活函数
        return output

看上面的代码的话，其实只需要看get_output()函数，就知道maxout的实现了。所以说有的时候，一篇文献的代码，其实就只有几行代码，maxout就仅仅只有一行代码而已：

output = K.max(K.dot(X, self.W) + self.b, axis=1)
#maxout激活函数

3. 理论上与传统激活函数对比

Maxout可以看成是一个激活函数 ，然而它与原来我们以前所学的激活函数又有所不同。传统的激活函数：

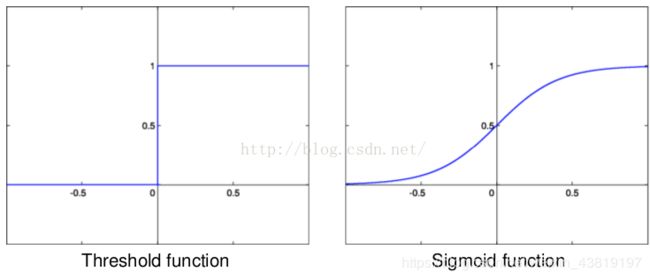
比如阈值函数、S函数等。maxout激活函数，它具有如下性质：

1、maxout激活函数并不是一个固定的函数，不像Sigmod、Relu、Tanh等函数，是一个固定的函数方程
2、它是一个可学习的激活函数，因为我们W参数是学习变化的。
3、它是一个分段线性函数：

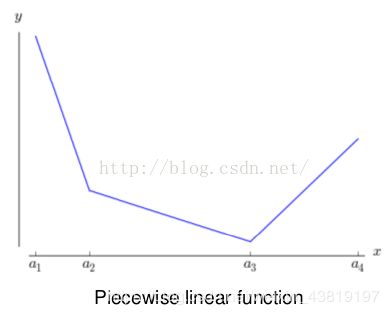
然而任何一个凸函数，都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数：relu、abs激活函数，看成是分成两段的线性函数，如下示意图所示：

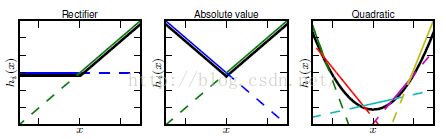
maxout的拟合能力是非常强的，它可以拟合任意的的凸函数。最直观的解释就是任意的凸函数都可以由分段线性函数以任意精度拟合（学过高等数学应该能明白），而maxout又是取k个隐隐含层节点的最大值，这些”隐隐含层"节点也是线性的，所以在不同的取值范围下，最大值也可以看做是分段线性的（分段的个数与k值有关）
maxout是一个函数逼近器，对于一个标准的MLP网络来说，如果隐藏层的神经元足够多，那么理论上我们是可以逼近任意的函数的。类似的，对于maxout 网络也是一个函数逼近器。