（二）永磁同步电机矢量控制（三电平）——三电平传统SVPWM调制算法原理

  各位同学你们好呀，上期我们讲了中性点钳位型的三电平逆变器原理，相信大家都有印象了。那么这一期我们要详解三电平传统SVPWM调制算法原理。通过学习后，希望能给初学者提供捷径明白算法原理，将来做仿真研究或者工程实际应用能快速上手。

可能有些同学对SVPWM是零基础的，为了能够使大家快速入门，这期我们分三部分内容来写：

1. 什么是空间矢量调制（SVPWM）。到底有什么意义？
2. 三电平SVPWM算法原理。可能有些人会问，怎么一下子就说三电平的？我两电平都还没搞清楚呢。不用担心，我在讲的时候会提到两电平的，三电平的会了两电平的自然就会！！！这部分的内容原理比较多，包括扇区判断、区域判断、时间计算和时间状态分配。
3. 总结。

---

进入正文！！

---

1 什么是空间矢量调制（SVPWM）

SVPWM这种调制方法是专门应用在电机控制上的，目的是为了获得幅值恒定的旋转圆形磁场，这样电机才能稳定运行。

那怎样才能够产生圆形的旋转磁场呢？学过高等数学（复变函数与积分变换）的同学都知道，圆周运动对应在直线上投影就是正弦波。

动画清晰的描述了正弦波与圆周运动有内在联系。那么只要控制磁链以恒定的角速度w做圆周运动就行了，对应的说，控制磁链以恒定的角速度w做正弦变化。由电机定子电压方程式可知，定子电压和磁链有对应关系，当各相电压和磁链合成在一起后，化简为如下：

其中us定子三相电压合成矢量，Rs是定子电阻，Is是定子三相电流合成矢量，Ψs是定子三相磁链合成矢量。当电机转速不是很低的时候，定子电阻压降可以忽略不计，化简为如下：

给出磁链矢量Ψs的表达式，如下：

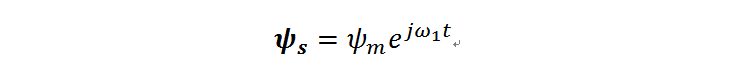
其中Ψm是磁链Ψs的幅值，w1是磁链角速度。将此式进行求导可得出电压矢量us的表达式：

由此可知，当磁链大小固定时，电压矢量的幅值和角速度w1成正比，且方向与磁链方向正交。

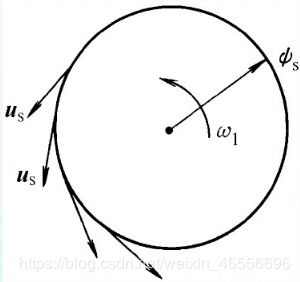
最终，想要控制磁链轨迹为圆形就转化为控制电压矢量轨迹为圆形。

总结：在一个输出周期内，通过控制三相电压所合成的电压矢量为圆轨迹的调制方式就是空间矢量调制（SVPWM）。

---

2 三电平SVPWM算法原理

既然明白了要使合成电压矢量为圆轨迹，那具体应该如何才能做到？这就涉及到算法原理。

以中性点钳位型三电平逆变器为主电路。上一期总结过，该电路有三种工作状态：高电平p、零电平o和低电平n。

由于三相电路由三个相同的电路结构组成，那么合起来工作状态组合有3^3=27种。因此，在基于三相ABC坐标系下，可以画出三电平的空间矢量图。

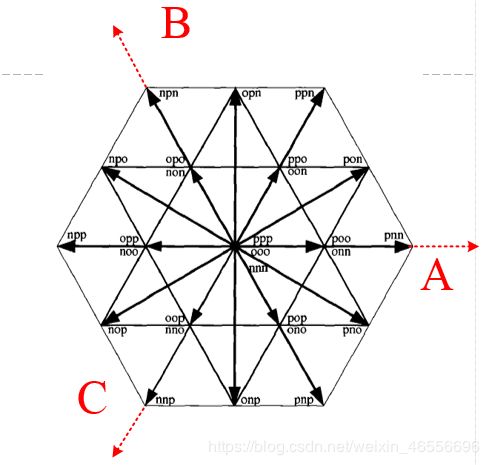
从图中可以看出，实际上独立的电压矢量只有19个，称为“基本电压矢量”，剩下8个称为“冗余矢量”。基本矢量有长有短，分下类：零矢量、短矢量、中矢量和长矢量。为了使三电平逆变器输出的电压矢量为圆形，可以选择三个基本电压矢量来等效。

等效的原理是根据伏秒平衡原则，假设选取基本电压矢量为V1、V2和V3，那么基本电压矢量与合成电压参考矢量有以下关系：

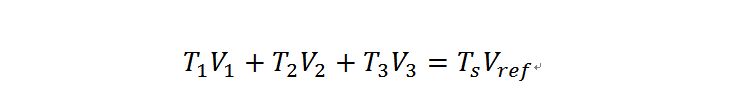
其中T1、T2、T3为对应的作用时间，Ts是采样时间。因此，当采样时间Ts足够小，所合成的电压参考矢量在一个输出周期内越接近圆。

那么三电平SVPWM的基本电压矢量该如何选择？这个是需要几个判断步骤的，依次为：扇区判断、区域判断、时间计算和时间状态分配。
（注意：两电平的SVPWM所画出的空间矢量状态图只有一层六边形，所以不用区域判断，很方便吧！！）

2.1 扇区判断

将空间矢量图按60°来划分区域，分为六个扇区，分别为I、II、III、IV、V、VI表示扇区号，且每个扇区的角度为60°。

因此可以按照基于A相坐标下的参考电压矢量的角度来判断其所在的扇区位置。具体判断如下：

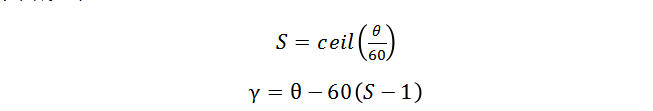
其中ceil函数表示向上取整；S表示扇区位置；θ表示参考电压矢量的辐角；γ表示参考电压矢量在对应扇区位置的角度。

2.2 区域判断

区域判断的目的主要是找出该扇区内合成参考电压矢量的三个基本矢量。传统三电平SVPWM方法是将每个扇区分为6个区域，分别用1,2,3,4,5,6表示区域号。

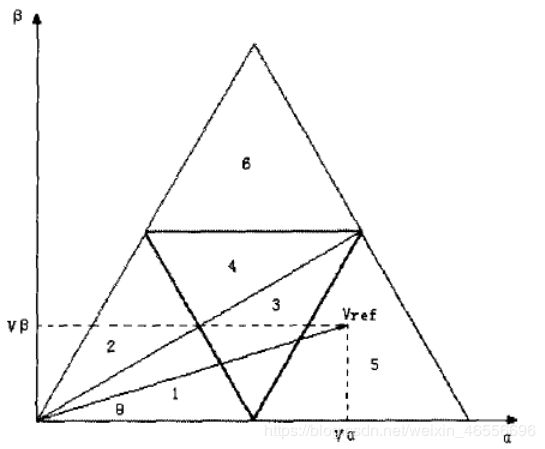
将参考电压矢量Vref在α轴和β轴上的投影分别为Vα和Vβ，角度为θ。根据几何知识可知，判断参考电压矢量所在区域：

确定好区域位置后，根据最近三角形矢量法则（选取三角形内的三个顶点），就能够找到对应三个基本电压矢量。

为了更直观点给大家看明白，对应上面的图，列了个表格如下：

2.3 时间计算

找到基本矢量之后就需要确定每个矢量的作用时间，来合成等效参考电压矢量。假设所找到的三个基本矢量为V1，V2，V3，连同参考电压矢量Vref一起，根据伏秒平衡，则：

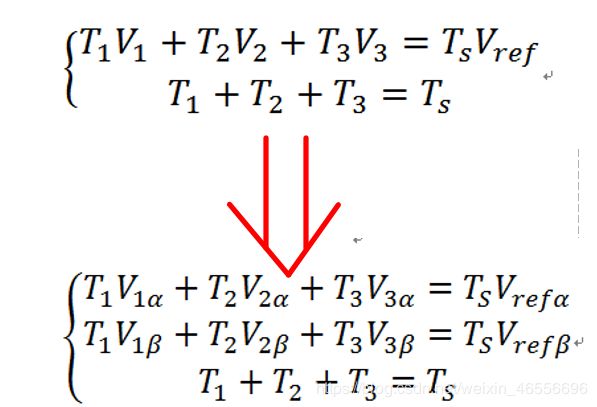
由于上面式子，一共有三个方程式。那么根据矩阵分析知识，即可求得线性方程组的解T1、T2、T3。当然也可以用几何知识来求解，不过比较麻烦，但前人比较牛B，已经用几何知识推出了所有区域的解。

2.4 时间状态分配

知道了基本电压矢量和作用时间。那如何分配才能较好的等效为合成参考矢量？？这里有两种方法：第一是五段式；第二是七段式。一般来说七段式方法效果更好。

七段式有以下分配原则：

• 三个基本矢量中，以较短矢量作为起始矢量。
• 任意一次电压矢量的变化，只允许只有一相的电路状态发生改变。这样做是为了降低开关损耗。

以区域1为例，七段式矢量排序为： V2→V3-→V1→V2→V1→V3→V2。

对应的时间分配如下图所示：

根据以上分配方式，依次推导出所有区域的矢量状态排序。

最终，我们只需要根据基本电压矢量来确定开关管状态即可，从而完成SVPWM输出。

3 总结

通过这期学习后，应该都明白什么是SVPWM了，大家可以根据这个算法原理去尝试搭建个三电平SVPWM模块。如果觉得在区域判断那里用几何知识搭建很复杂的话，可以用矩阵的方法来搭。希望本文能够帮助到大家，下一期就介绍三电平仿真总体模型和仿真结果。

更详细的讲解请关注公众号：电力电子学社

之后会陆续开放仿真模型下载喔~敬请关注！