数据结构_队列及其应用

除了顺序容器外，标准库还定义了三个顺序容器适配器，stack、queue和priority_queue。本质上一个适配器是一种机制，能使某种事物的行为看起来像另外一种事物一样。一个容器适配器接收一种已有的容器类型，使其行为看起来像另外一种不同类型一样。
本文主要介绍队列及其应用，栈及其应用参考栈及其应用 ，优先级队列参考

队列

/*queue默认基于deque实现，也可以使用list或vector事项*/
q.pop();  //删除队首元素，并返回
q.empty();
q.push();
q.front();
q.back();

1、银行服务模拟
以银行这一典型场景为例，使用队列实现顾客服务的调度优化。

struct Customer
{
    int window;                  //所属窗口
    unsigned int time;           //其所办业务的服务时长
};

/*模拟银行中接收服务的整个过程,根据银行所设窗口的数量相应的建立多个队列，以单位时间为间隔反复迭代直至下班*/
void simulate ( int nWin, int servTime ) { //按指定窗口数、服务总时间模拟银行业务
    Queue* windows = new Queue[nWin]; //为每一窗口创建一个队列
    for ( int now = 0; now < servTime; now++ ) { //在下班之前，每隔一个单位时间
       if ( rand() % ( 1 + nWin ) ) { //新顾客以nWin/(nWin + 1)的概率到达
          Customer c ; c.time = 1 + rand() % 98; //新顾客到达，服务时长随机确定
          c.window = bestWindow ( windows, nWin ); //找出最佳（最短）的服务窗口
          windows[c.window].push ( c ); //新顾客加入对应的队列
       }
       for ( int i = 0; i < nWin; i++ ) //分别检查
          if ( !windows[i].empty() ) //各非空队列
             if ( -- windows[i].front().time <= 0 ) //队首顾客的服务时长减少一个单位
                windows[i].pop(); //服务完毕的顾客出列，由后继顾客接替
    } //for
    delete [] windows; //释放所有队列（此前，~List()会自动清空队列）
 }

/*每一个时刻都有一位顾客按一定的概率抵达，随机确定所办业务的时长之后，归入某一最优的队列*/
 int bestWindow ( Queue windows[], int nWin ) { //为新到顾客确定最佳队列
    int minSize = windows[0].size(), optiWin = 0; //最优队列（窗口）
    for ( int i = 1; i < nWin; i++ ) //在所有窗口中
       if ( minSize > windows[i].size() ) //挑选出
          { minSize = windows[i].size(); optiWin = i; } //队列最短者
    return optiWin; //返回
 }

2、使用两个栈实现一个队列
题目：用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }

    int pop() {
        //stack2没有元素时将stack1中的元素弹入stack2
        if(stack2.size()<=0)
        {
            while(stack1.size()>0)
            {
                int &i=stack1.top();
                stack1.pop();
                stack2.push(i);
            }
        }
        int &j=stack2.top();
        stack2.pop();
        return j;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

上述的基本步骤：当stack2中不为空时，在stack2中的栈顶元素时最先进入队列的元素，可以弹出。如果stack2为空时，我们把stack1中的元素逐个弹出压入栈stack2中。

3、滑动窗口的最大值
题目：给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

对于这种如果采用蛮力算法很容易就可以解决：可以扫描每一个滑动窗口的所有数字并找出其中的最大值。如下：

class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        //暴力解出来
        vector<int> max;
        if(num.size()>=size&&size>=1)
        {
            for(int i=0;i1;++i)
            {
                int m=num[i];
                for(int j=i+1;jif(num[j]>m)
                        m=num[j];
                }
                max.push_back(m);
            }
        }
        return max;
  }
};

其实滑动窗口可以看成是一个队列，如果我们可以在队列中找到他的最大数，就可以解决。在栈及其应用 中的说明了如何实现用o(1)的时间得到最小值的栈，并且上面实现了用两个栈实现一个队列，综合，我们可以把队列用两个栈实现，可以用o(1)时间找到栈中的最大值，就可以用0(1)时间找到队列的最小值。

这里使用另外一种思路：并不把滑动窗口的每个数值都存入队列中，而是只把有可能成为滑动窗口最大的值存入一个双端口队列。

class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        vector<int> max;
        if(num.size()>=size&&size>=1)
        {
            deque<int> index;
            for(int i=0;iwhile(index.size()&&num[i]>=num[index.back()])
                    index.pop_back();
                index.push_back(i);
            }
            for(int i=size;i//从后面依次弹出队列中比当前num值小的元素，同时也能保证队列首元素为当前窗口最大值下标
                while(index.size()&&num[i]>=num[index.back()])
                    index.pop_back();
                //当当前窗口移出队首元素所在的位置，即队首元素坐标对应的num不在窗口中，需要弹出
                while(index.size()&&index.front()<=(i-size))
                    index.pop_front();
                index.push_back(i);
            }
            max.push_back(num[index.front()]);
        }
        return max;
    }
};

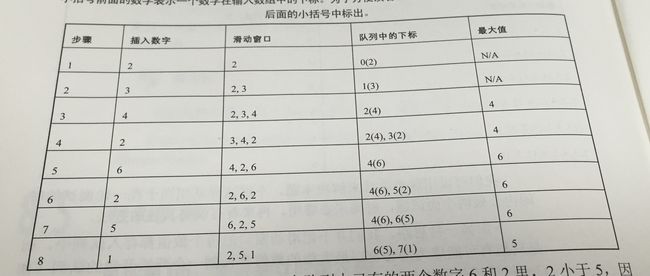
上述代码中，index是一个两端开口的队列，用来保存有可能是滑动窗口最大值的数字的下标。在存入一个数字之前，首先要判断队列里已有的数字是否小于待存入数字。如果小于将把它们从队列的尾部删除，这些数字已经不可能是窗口的最大值。同时如果队列头部的数字已经从窗口滑出，滑出的数字也要从队列的头部删除。