SVM原理和SOM算法总结

1 原问题

约定：Data=${(x_i,y_i)}_{i=1}^N,x_i\in R^p,y_i\in \{1,-1\}$,

则SVM变为如下的最优化问题：

(1)$\{\begin{array}{l}min\frac{1}{2}{w}^{T}w\\ s.t.y_i(w^T{x}_i+b)\ge 1⟺1-y_i(w^T{x}_i+b)\le 0\end{array}$

令$\mathcal{L}(w,b,\alpha )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\alpha }_i(1-y_i(w^T{x}_i+b))$,
这里${\alpha }_i\ge 0,1-y_i(w^T{x}_i+b)\le 0.$

下面证明问题(1)等价于下面的问题$(P)$.

$(P)\{\begin{array}{l}\underset{w,b}{\min }\underset{\alpha }{\max }\mathcal{L}(w,b,\alpha )\\ s.t.{\alpha }_i\ge 0\end{array}$

证明：讨论两种情况：

如果$1-y_i(w^T{x}_i+b)\ge 0$,又由于${\alpha }_i\ge 0$，所以,
$\underset{\alpha }{\max }\mathcal{L}(w,b,\alpha )=\frac{1}{2}{w}^{T}w+\infty =\infty$.

如果$1-y_i(w^T{x}_i+b)\le 0$,则$\underset{\alpha }{\max }\mathcal{L}(w,b,\alpha )=\frac{1}{2}{w}^{T}w+0=\frac{1}{2}{w}^{T}w$.

综上，$\underset{w,b}{\min }\underset{\alpha }{\max }\mathcal{L}(w,b,\alpha )=\underset{w,b}{\min }\{\infty ,\frac{1}{2}{w}^{T}w\}=\frac{1}{2}{w}^{T}w.证毕$

2 对偶问题

弱对偶定理:$\underset{w,b}{\min }\underset{\alpha }{\max }\mathcal{L}(w,b,\alpha )\ge \underset{\lambda }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )$.

强对偶定理:$\underset{w,b}{\min }\underset{\alpha }{\max }\mathcal{L}(w,b,\alpha )=\underset{\lambda }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )$.

由于原问题$(P)$目标函数是二次函数(凸函数),约束条件是线性，所以对于问题$(P)$，强对偶定理成立。

即原问题$(P)$等价于下面的对偶问题(D):

(D)$\{\begin{array}{l}\underset{\alpha }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )\\ s.t.{\alpha }_i\ge 0\end{array}$

3对偶问题的求解

(D)$\{\begin{array}{l}\underset{\alpha }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )\\ s.t.{\alpha }_i\ge 0\end{array}$

先来求$\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )$，这时需要$\mathcal{L}(w,b,\alpha )$函数分别对w,b求导如下。

$\frac{\partial L}{\partial b}=\frac{\partial }{\partial b}(-\sum _{i=1}^N{\alpha }_i{y}_{i}b)=-\sum _{i=1}^N{\alpha }_i{y}_i=0$,即$\sum _{i=1}^N{\alpha }_i{y}_i=0$.

将其带入$\mathcal{L}(w,b,\alpha )$得，

$\begin{array}{ll}\mathcal{L}(w,b,\alpha )& =\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i(w^T{x}_i+b)\\ & =\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^N{\alpha }_i{y}_{i}b\\ & =\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{w}^T{x}_i\end{array}.$

$\frac{\partial \mathcal{L}}{\partial w}=\frac{1}{2}\cdot 2\cdot w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0⟹w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$.

再将上式带入$L$中得，

$\begin{array}{ll}\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )& =\frac{1}{2}(\sum _{i=1}^N{\alpha }_i{y}_i{x}_i{)}^T(\sum _{i=1}^N{\alpha }_i{y}_i{x}_i)-\sum _{i=1}^N{\alpha }_i{y}_i(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j{)}^T{x}_i+\sum _{i=1}^N{\alpha }_i\\ & =\frac{1}{2}\sum _{i=1}^N{\alpha }_i{y}_i{x}_i^T\sum _{j=1}^N{\alpha }_j{y}_j{x}_j-\sum _{i=1}^N{\alpha }_i{y}_i\sum _{j=1}^N{\alpha }_j{y}_j{x}_j^T{x}_i+\sum _{i=1}^N{\alpha }_i\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_j^T{x}_i+\sum _{i=1}^N{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\alpha }_i\end{array}$,

，上面用到了$x_i^T\cdot x_j=x_j^T\cdot x_i$.

综上，问题(D)等价于下面的$(D_1)$:

$(D_1)\{\begin{array}{l}\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\alpha }_i\\ s.t.{\alpha }_i\ge 0\\ \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$

事实上，在SVM中经常使用核函数来将输入映射到高维空间，内积只是核函数的一种。我们把$x_i,x_j$的内积$x_i^T{x}_j$改为$K(x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$，则(D2)变为：
$(D_1^{\prime })\{\begin{array}{l}\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)+\sum _{i=1}^N{\alpha }_i\\ s.t.{\alpha }_i\ge 0\\ \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$

此时，与上面类似，我们有$w=\sum _{i=1}^N{\alpha }_i{y}_i\varphi (x_i).$

4 KKT条件

考虑如下一般形式的约束优化问题：

$\{\begin{array}{l}\min f(x),\\ s.t.g_i(x)\le 0,i=1,2,\cdots ,m,\\ h_i(x)=0,i=1,2,\cdots ,\ell .\end{array}$

假设$x^{\ast }$是原问题的局部最优解，且$x^{\ast }$处某个"适当的条件(constraint qualification, 也称约束规范)"成立，则存在$\alpha ,\mu$使得,

$$\begin{array}{r}\nabla f(x^{\ast })+\sum _{i=1}^m{\alpha }_i\nabla g_i(x^{\ast })-\sum _{j=1}^{\ell }{\mu }_j\nabla h_j(x^{\ast })=0\\ {\alpha }_i\ge 0,i=1,2,\cdots m,\\ g_i(x^{\ast })\le 0,i=1,2,\cdots ,m,\\ h_j(x^{\ast })=0,i=1,2,\cdots ,\ell ,\\ {\alpha }_i{g}_i(x^{\ast })=0,i=1,2,\cdots ,m.\end{array}$$
，以上5条称为Karush-Kuhn_Tucker(KKT)条件。
对于SVM的对偶问题：
(D)$\{\begin{array}{l}\underset{\alpha }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )\\ s.t.{\alpha }_i\ge 0\end{array}$
其中，$\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )$对应的KKT条件为:
$$\{\begin{array}{l}\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0\\ 1-y_i(w^T{x}_i+b)\le 0,\\ {\alpha }_i\ge 0,\\ {\alpha }_i(1-y_i(w^T{x}_i+b)=0.\end{array}$$
最后一条称为互补松弛条件(slackness complenmentary)。
注意：对于$1-y_i(w^T{x}_i+b)<0$的点，要想互补松弛条件成立，${\alpha }_i=0$必须成立。即，对于非支撑向量，$\alpha$的值都为0. 也就是说，对于目标函数$L$来说，真正起作用的只有支撑向量。
前面我们已经求出$w^{\ast }=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$，下面我们来求b。
由前面分析，存在支撑向量$(x_k,y_k)$使得$1-y_k(w^T{x}_k+b)=0$，即$y_k(w^T{x}_k+b)=1\Rightarrow y_k^2(w^T{x}_k+b)=w^T{x}_k+b=y_k$。
从而，$b^{\ast }=y_k-w^T{x}_k=y_k-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i^T{x}_k$。

注意:(1)$\alpha$在非支撑向量上都为0，所有的非零$\alpha$只有在支撑向量才会出现。
(2) 对于使用核函数的情况，$w^{\ast }=\sum _{i=1}^N{\alpha }_i{y}_i\varphi (x_i)$,$b^{\ast }=y_k-\sum _{i=1}^N{\alpha }_i{y}_{i}K(x_i,x_k)$.

上面我们已经求出$w^{\ast },b^{\ast }$的值，但是这两个式子都有未知量$\alpha$, 所以还需要首先求出$\alpha$的值。这就要用到SMO算法。

5 软间隔SVM

经过加入松弛变量 ${\xi }_i$ 后，模型修改为：

$(2)\{\begin{array}{l}min\frac{1}{2}{w}^{T}w+C\sum _{i=1}^N{\xi }_i\\ s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i\\ {\xi }_i\ge 0\end{array}$
将其转化为：
$(P_2)\{\begin{array}{l}\underset{w,b,\xi }{\min }\underset{\alpha ,\mu }{\max }\mathcal{L}(w,b,\alpha ,\mu )=\frac{1}{2}{w}^{T}w+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i(y_i(w^T{x}_i+b)-1+{\xi }_i)-\sum _{i=1}^N{\mu }_i{\xi }_i\\ s.t.\forall i,{\alpha }_i\ge 0\\ \forall i,{\mu }_i\ge 0\end{array}$
对应的对偶问题为：
$(D_2)\{\begin{array}{l}\underset{\alpha ,\mu }{\max }\underset{w,b,\xi }{\min }\mathcal{L}(w,b,\alpha ,\mu )=\frac{1}{2}{w}^{T}w+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i(y_i(w^T{x}_i+b)-1+{\xi }_i)-\sum _{i=1}^N{\mu }_i{\xi }_i\\ s.t.\forall i,{\alpha }_i\ge 0\\ \forall i,{\mu }_i\ge 0\end{array}$
其中，$\underset{w,b,\xi }{\min }\mathcal{L}(w,b,\alpha ,\xi )$对应的KKT条件为：
$\{\begin{array}{l}\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0,\frac{\partial L}{\partial \xi }=0\\ y_i(w^T{x}_i+b)-1+{\xi }_i\ge 0\\ {\xi }_i\ge 0\\ {\alpha }_i\ge 0,{\mu }_i\ge 0\\ {\alpha }_i(y_i(w^T{x}_i+b)-1+{\xi }_i)=0\\ {\mu }_i{\xi }_i=0\end{array}$
其中，第一个条件可化为：
$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i,0=\sum _{i=1}^N{\alpha }_i{y}_i,{\alpha }_i=C-{\mu }_i$.

将这些等式带入，可以得到下面的等价问题：

$(D_2^{\prime })\{\begin{array}{l}\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\alpha }_i\\ s.t.0\le {\alpha }_i\le C\\ \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$

令$f(x)=w^{T}x+b$，从得到的结果逆向推理，可以得到下面的式子：

$\begin{array}{l}{\alpha }_i=0\to {\mu }_i=C\to {\xi }_i=0\to y_{i}f(x_i)\ge 1\\ 0<{\alpha }_i<C\to {\mu }_i\ne 0\to {\xi }_i=0\to {\alpha }_i(y_{i}f(x_i)-1)=0\to y_{i}f(x_i)=1\\ {\alpha }_i=c\to {\mu }_i=0\to {\xi }_i\ge 0\to {\alpha }_i(y_{i}f(x_i)-1+{\xi }_i)=0\to y_{i}f(x_i)\le 1.\end{array}$

6 SMO算法

现在我们的问题就是，如何快速的求解下面这个优化问题。
$(D_3)\{\begin{array}{l}\underset{a}{\min }\frac{1}{2}\sum _{i=1}^N\sum _{i=1}^N{y}_i{y}_j{x}_i^T{x}_j{\alpha }_i{\alpha }_j-\sum _{i=1}^N{\alpha }_i\\ s.t.0\le {\alpha }_i\le C\\ \sum _{i=1}^N{y}_i{\alpha }_i=0\end{array}$
写成核函数形式为：
$(D_3^{\prime })\{\begin{array}{l}\underset{a}{\min }\frac{1}{2}\sum _{i=1}^N\sum _{i=1}^N{y}_i{y}_{j}K(x_i,x_j){\alpha }_i{\alpha }_j-\sum _{i=1}^N{\alpha }_i\\ s.t.0\le {\alpha }_i\le C\\ \sum _{i=1}^N{y}_i{\alpha }_i=0\end{array}$
解决带不等式限制的凸优化问题，采取的一般都是内点法。但是内点法的代价太大，需要存储一个$N^2$的矩阵，在内存有限的条件下不可行，且每次求全局导数花费时间很多，此外还牵涉到数值问题。而SMO是解决二次优化问题的神器。他每次选择两个拉格朗日乘子${\alpha }_i,{\alpha }_j$来求条件最小值，然后更新${\alpha }_i,{\alpha }_j$。由于在其他拉格朗日乘子固定的情况下，${\alpha }_i,{\alpha }_j$有如下关系：
$$\sum _{i=1}^N{\alpha }_i{y}_i=0\to {\alpha }_i{y}_i+{\alpha }_j{y}_j=-\sum _{k\ne i,j}^N{\alpha }_k{y}_k.$$

这样${\alpha }_i$就可以通过${\alpha }_j$表示出来，此时优化问题可以转变为一个变量的二次优化问题，这个问题的计算量非常少。所以SMO包括两个过程，一个过程选择两个拉格朗日乘子，这是一个外部循环，一个过程来求解这两个变量的二次优化问题，这个是循环内过程。我们先来解决两个变量的lagrange multipliers问题，然后再去解决乘子的选择问题。

6.1 ${\alpha }_i,{\alpha }_j$的计算

由SVM优化目标函数的约束条件$\sum _{i=1}^N{a}_i{y}_i=0$，可以得到：
$$a_1{y}_1+a_2{y}_2=-\sum _{j=3}^N{a}_j{y}_j\triangleq \zeta \to a_1=(\zeta -a_2{y}_2)y_1$$.
为了计算两个lagrange Multiplier的优化问题，SMO首先计算这两个乘子的取值范围，然后再这个范围限制下解决二次优化问题。为了书写方便，现在用1,2来代替i,j。这两个变量之间的关系为$a_1{y}_1+a_2{y}_2=\zeta$，下面这幅图生动形象的解释了这两个变量的关系。

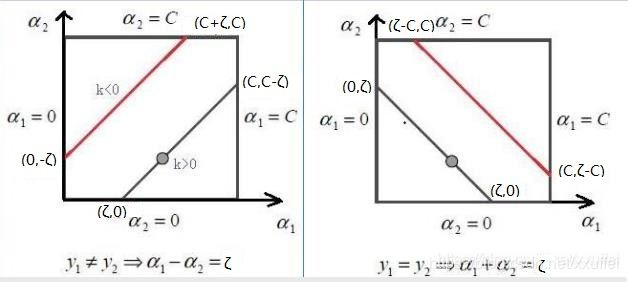
现在我们来讨论在进行双变量二次优化时${\alpha }_2$的取值范围。如果$y_1\ne y_2$，则${\alpha }_2$的下界L和上界H可以表示为:
$$L=\max (0,{\alpha }_2-{\alpha }_1),H=\min (C,C+{\alpha }_2-{\alpha }_1).(13-\text{Platt论文中编号})$$

反之，如果y1=y2，则${\alpha }_2$的下界L和上界H可以表示为:
$$L=\max (0,{\alpha }_2+{\alpha }_1-C),H=\min (C,{\alpha }_2+{\alpha }_1).(14-\text{Platt论文中编号})$$

对于上面的问题$(D_3^{\prime })$:

$(D_3^{\prime })\{\begin{array}{l}\underset{a}{\min }\frac{1}{2}\sum _{i=1}^N\sum _{i=1}^N{y}_i{y}_{j}K(x_i,x_j){\alpha }_i{\alpha }_j-\sum _{i=1}^N{\alpha }_i\\ s.t.0\le {\alpha }_i\le C\\ \sum _{i=1}^N{y}_i{\alpha }_i=0\end{array}$

首先，将原优化目标函数展开为与${\alpha }_1$和${\alpha }_2$有关的部分和无关的部分：
$\begin{array}{rl}\min \Phi ({\alpha }_1,{\alpha }_2)& =\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+a_1{y}_1\sum _{i=3}^N{\alpha }_i{y}_i{K}_{1i}+{\alpha }_2{y}_2\sum _{j=3}^N{\alpha }_j{y}_j{K}_{2j}+c)\\ & =\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+{\alpha }_1{y}_1{v}_1+{\alpha }_2{y}_2{v}_2+c)(1)\end{array}$,

其中$v_i=\sum _{j=3}^N{\alpha }_j{y}_j{K}_{ij}(i=1,2)$，c是与${\alpha }_1$和${\alpha }_2$无关的部分，在本次优化中当做常数项处理。

我们将优化目标中所有的${\alpha }_1$都替换为用${\alpha }_2$表示的形式，得到如下式子：
$\begin{array}{rl}\min \Phi ({\alpha }_2)=& \frac{1}{2}{K}_{11}(\zeta -{\alpha }_2{y}_2{)}^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_2{K}_{12}{\alpha }_2(\zeta -{\alpha }_2{y}_2)-\\ & y_1(\zeta -{\alpha }_2{y}_2)-{\alpha }_2+(\zeta -{\alpha }_2{y}_2)\sum _{i=3}^N{\alpha }_i{y}_i{K}_{1i}+{\alpha }_2{y}_2\sum _{j=3}^N{\alpha }_j{y}_j{K}_{2j}+c\\ =& \frac{1}{2}{K}_{11}(\zeta -{\alpha }_2{y}_2{)}^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_2{K}_{12}{\alpha }_2(\zeta -{\alpha }_2{y}_2)-\\ & y_1(\zeta -{\alpha }_2{y}_2)-{\alpha }_2+(\zeta -{\alpha }_2{y}_2)v_1+{\alpha }_2{y}_2{v}_2+c.(2)\end{array}$.

此时，优化目标中仅含有${\alpha }_2$一个待优化变量了，现在将待优化函数对${\alpha }_2$求偏导得到如下结果：

$\begin{array}{rl}\frac{\partial \Phi ({\alpha }_2)}{\partial {\alpha }_2}=& (K_{11}+K_{22}-2K_{12})alph{a}_2-K_{11}\zeta y_2+K_{12}\zeta y_2+y_1{y}_2-1-y_2\sum _{i=3}^N{a}_i{y}_i{K}_{1i}+y_2\sum _{j\ne 1,2}^N{\alpha }_j{y}_j{K}_{2j}\\ =& (K_{11}+K_{22}-2K_{12}){\alpha }_2-K_{11}\zeta y_2+K_{12}\zeta y_2+y_1{y}_2-1-y_2{v}_1+y_2{v}_2(3)\end{array}$.

前面我们已经定义SVM超平面的模型为$f(x)=w^{T}x+b$，将已推导出w的表达式带入得
$f(x)=\sum _{i=1}^N{\alpha }_i{y}_{i}K(x_i,x)+b;f(x_i)$表示样本$x_i$的预测值，$y_i$表示样本$x_i$的真实值，定义$E_i$表示预测值与真实值之差为$E_i=f(x_i)-y_i$，从而，
$v_i=\sum _{j=3}^N{\alpha }_i{y}_i{K}_{ij},i=1,2$，因此，
$\begin{array}{rl}{v}_1& =f(x_1)-\sum _{j=1}^2{y}_j{\alpha }_j{K}_{1j}-b=f(x_1)-y_1{\alpha }_1{K}_{11}-y_2{\alpha }_2{K}_{12}-b(4)\\ v_2& =f(x_2)-\sum _{j=1}^2{y}_j{\alpha }_j{K}_{2j}-b=f(x_2)-y_1{\alpha }_1{K}_{21}-y_2{\alpha }_2{K}_{22}-b(5)\end{array}$.

优化前的解记为${\alpha }_1^{old},{\alpha }_2^{old}$，更新后的解记为${\alpha }_1^{new},{\alpha }_2^{new}$，则(1),(4),(5)可得，

$$\{\begin{array}{l}{a}_1^{old}{y}_1+a_2^{old}{y}_2=\zeta \\ \sum _{i=3}^N{\alpha }_i{y}_i{K}_{1i}=f(x_1)-y_1{\alpha }_1^{old}{K}_{11}-y_2{\alpha }_2^{old}{K}_{12}+b\\ \sum _{j=3}^N{\alpha }_j{y}_j{K}_{2j}=f(x_2)-y_1{\alpha }_1^{old}{K}_{21}-y_2{\alpha }_2^{old}{K}_{22}+b\end{array}$$

将以上三个条件带入偏导式子中，得到如下结果：

$\begin{array}{rl}\frac{\partial \Phi ({\alpha }_2)}{\partial {\alpha }_2}& =(K_{11}+K_{22}-2K_{12})alph{a}_2-(K_{11}-K_{12})({\alpha }_1^{old}{y}_1+{\alpha }_2^{old}{y}_2)y_2\\ & +y_1{y}_2-1-y_2(u(x_1)-y_1{\alpha }_1^{old}{K}_{11}-y_2{\alpha }_2^{old}{K}_{12}-b)\\ & +y_2(u(x_2)-y_1{\alpha }_1^{old}{K}_{21}-y_2{\alpha }_2^{old}{K}_{22}-b)=0\end{array}$.

化简后得：

$(K_{11}+K_{22}-2K_{12}){\alpha }_2=(K_{11}+K_{22}-2K_{12}){\alpha }_2^{old}+y_2[(f(x_1)-y_1)-(f(x_2)-y_2)]$

记：$\eta =K_{11}+K_{22}-2K_{12}$, 则得到${\alpha }_2$的更新公式：

$${\alpha }_2^{new}={\alpha }_2^{old}+\frac{y_2(E_1-E_2)}{\eta }$$,
但是，我们还需要考虑${\alpha }_2$的取值范围，所以我们最后得到的${\alpha }_2$的新值为：
$${\alpha }_2^{new,clip}=\{\begin{array}{rl}H& if{\alpha }_2^{new}\ge H\\ {\alpha }_2^{new}& ifL<a_2^{new}<H\\ L& if{\alpha }_2^{new}\le L\end{array}(6)$$

由${\alpha }_1^{old}{y}_1+{\alpha }_2^{old}{y}_2={\alpha }_1^{new}{y}_1+{\alpha }_2^{new}{y}_2=C$可得${\alpha }_1$的更新公式：
$${\alpha }_1^{new}={\alpha }_1^{old}+y_1{y}_2({\alpha }_2^{old}-{\alpha }_2^{new,clip})(7)$$.

6.2 ${\alpha }_1,{\alpha }_2$取临界情况

大部分情况下，有$\eta =K_{11}+K_{22}-2K_{12}>0$。但是在如下几种情况下，${\alpha }_2^{new}$需要取临界值L或者H:

• η<0，当核函数K不满足Mercer定理（ Mercer定理:任何半正定对称函数都可以作为核函数）时，矩阵K非正定；
• η<0，样本x1与x2输入特征相同；

也可以如下理解，(3)式对${\alpha }_2$再求导，或者说(2)式中$\Phi ({\alpha }_2)$对${\alpha }_2$求二阶导数就是$\eta =K_{11}+K_{22}-2K_{12}>0$，

• 当η<0时，目标函数为凸函数，没有极小值，极值在定义域边界处取得。
• 当η=0时，目标函数为单调函数，同样在边界处取极值。

计算方法如下：
将${\alpha }_2^{new}=L$和${\alpha }_2^{new}=H$分别带入(7)式中，计算出${\alpha }_1^{new}=L_1$和${\alpha }_1^{new}=H_1$，其中$L_1={\alpha }_1+s({\alpha }_2-L),H_1={\alpha }_1+s({\alpha }_2-H)$.
将其带入目标函数(1)内，比较${\Psi }_L\triangleq \Psi ({\alpha }_1=L_1,{\alpha }_2=L)$与${\Psi }_H\triangleq \Psi ({\alpha }_1=H_1,{\alpha }_2=H)$的大小，${\alpha }_2$取${\Psi }_L$和${\Psi }_H$中较小的函数值对应的边界点，${\Psi }_L$和${\Psi }_H$计算如下：

$\begin{array}{rl}{\Psi }_L& =L_1{f}_1+L{f}_2+\frac{1}{2}{L}_1^2{K}_{11}+\\ {\Psi }_H& \end{array}$