机器学习算法调优的一般步骤

引言

假设我们实现了一个机器学习算法用于做分类，但在测试集上结果不好，下一步应该怎么办呢？有没有一些一般性的指导原则对我们的算法调优进行指导？

除了模型本身的一些参数调节，大部分人都知道去尝试下面一些通用的调整方法：

• 增加训练集
• 减少特征维度（从已有的特征中挑选出一部分）
• 增加新特征
• 增加多项式元素（比如将特征平方后叠加到原特征上，相当于增加了非线性的输入）
• 减小正则化参数的 λ 值
• 增大正则化参数的 λ 值

正如Andrew NG在机器学习课程上所说，上面提到的每一个方法，都可以扩展成一个6个月的项目；而大部分人都是凭直觉选择这些方法的，这浪费了大量的调优时间。有没有科学的指导原则来帮助我们选择这些通用的调整方法呢？

本文就以线性回归为例，详细讲解如何选择这些通用的调整方法，得出的结论也适用于其他的机器学习算法。下面先介绍正则化的作用。

正则化

这里先引入正则化的概念。

直观理解

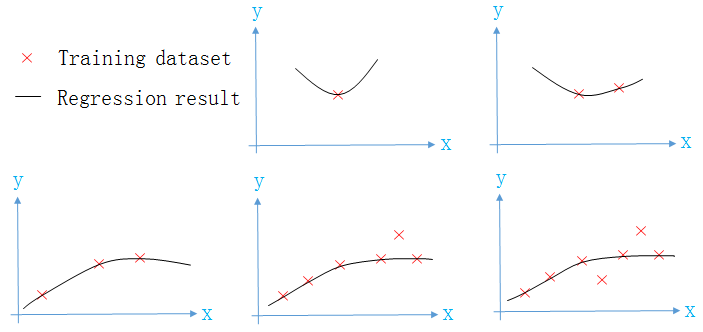
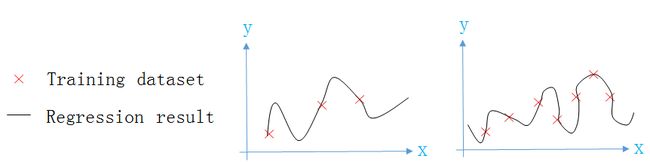
两个模型的回归曲线如下图所示，从图中可以看出，第二个模型已经过拟合(overfitting)。

如果我们减小 θ3,θ4 的值，就让第二个模型“接近”第一个模型，从而减少了第二个模型过拟合的程度。正则化要做的，就是适当减小 θ3,θ4 的值。

正则化定义

正则化参数 λ ，就是在原代价函数上，再叠加 λ 倍的 θ1 θn 。

J(θ)=12m[∑1m(h(x(i))−y(i))2+λ∑2nθ2j]

λ 越大，就能越大的调整模型过拟合的程度。

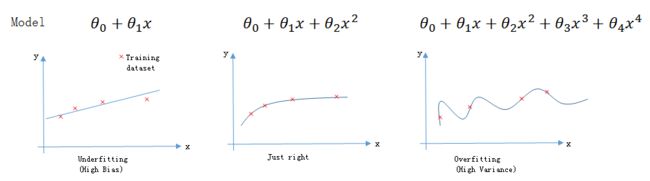
三种拟合的情况

• 欠拟合: 连训练集都不能很好的拟合，又叫High Bias
• Just Right: 能很好的拟合训练集与测试集
• 过拟合: 能很好的拟合训练集，但不能很好的拟合测试集，又叫High Variance

从下图可以直观的看出三种拟合情况之间的区别。

调优时，首先需要判断模型处于哪种拟合情况。怎么判断呢？就是划分训练集后，绘制Learning Curve即可。

训练集划分（train & validation & test）

一般按6:2:2的比例，将数据集分为训练集，验证集，测试集。
为什么需要验证集呢？

• 如果没有validation dataset，则可能训练出来的模型仅仅匹配测试集，而不适用于将来的数据。验证集能提高一定的泛化能力
• 验证集能保证模型训练到最优（比如可以用early stop策略）

Learning Curve(学习曲线)

Learning Curve是训练集误差与验证集误差相对于训练集数目m的二维曲线图。这里和下面的m，表示有多少个训练集。比如我有1000个手写数字训练样本，m=10，表示从中取10个做训练集；m=1000，表示从中取1000个做训练集。

训练集误差：是根据训练集predic结果h，与真实结果y计算得到的。

Jtrain=12m∑1m(h(x(i))−y(i))2

• 这里m是横轴，动态变化。

验证集误差：同理，是根据验证集结果计算得到的。

Jcv=12mcv∑1mcv(h(x(i))−y(i))2

• mcv是训练集个数，固定值。

将 Jtrain 与 Jcv 与m的关系画到二维图中，就得到了Learning Curve。

下面介绍三种拟合情况的Learning Curve。

Learning Curve of Just Right

假设Just Right情况下的线性模型为 hθ(x)=θ0+θ1x+θ2x2 。

下面是训练集个数m不同时，模型拟合训练集的情况。

可见

• 随着训练集数量m的增加，模型遇到的情况就越复杂，在训练集上的误差会逐渐增加，但都会保持在较小的一个范围内
• 随着训练集数量m的增加，模型见多识广，所以模型在验证集上的误差就逐渐减少，且越来越接近训练集误差

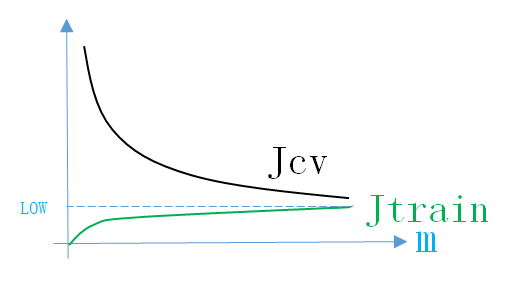
所以Just Right情况下的Learning Curve如下图所示

同理，画出Learning Curve后，如果满足上面的条件，就说明模型处于Just Right情况。说明模型的结构正确，接下来就不用调整结构参数，调节模型其它参数（正则化参数 λ ）即可。

Learning Curve of High Bias

假设High Bias情况下的线性模型为 hθ(x)=θ0+θ1x 。

下面是训练集个数m不同时，模型拟合训练集的情况。

可见

• 随着训练集数量m的增加，模型在训练集上的误差会逐渐增加，且误差会越来越大
• 随着训练集数量m的增加，模型在验证集上的误差会有所下降，误差依然很大，且越来越接近训练集误差

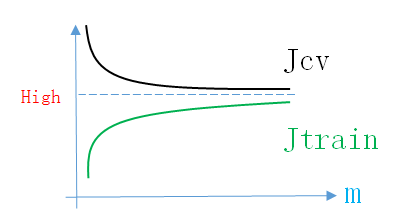
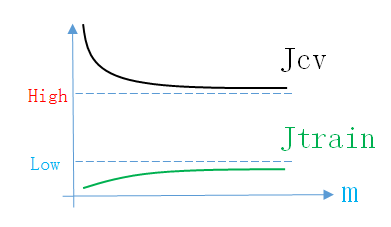
所以High Bias情况下的Learning Curve如下图所示

同理，画出Learning Curve后，如果满足上面的条件，就说明模型处于High Bias情况。说明模型的结构不正确，接下来就应该先调整结构参数（增加新feature，增加多项式项，减小正则化参数，增加神经网络隐层神经元个数）。

Learning Curve of High Variance

假设High Variance情况下的线性模型为 hθ(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4+θ5x5 。

下面是训练集个数m不同时，模型拟合训练集的情况。

可见

• 随着训练集数量m的增加，模型在训练集上的误差会逐渐增加（不可能拟合的天衣无缝），但由于模型的拟合能力较强，所以误差都会很小
• 随着训练集数量m的增加，模型在验证集上的误差会有所下降，但由于模型拟拟合能力强，把训练集上的毛刺都拟合了，所以误差依然很大，且与训练集误差有较大的差距。但验证集误差会随着m的增加而减少

所以High Variance情况下的Learning Curve如下图所示

同理，画出Learning Curve后，如果满足上面的条件，就说明模型处于High Variance情况。说明模型的结构不正确，接下来就应该先调整结构参数（减小feature数量，增加正则化参数，减小神经网络隐层神经元个数）。High Variance情况下，也可以采用增加m的方法使误差下降。

结论

综上，我们可以发现，对机器学习算法进行调优，首先要根据Learning Curve来判断模型处于哪种拟合情况，从而判断模型结构是否正确。调整时，先进行模型结构调整(feature数量，多项式元素)，让模型处于Just Right的情况，再调整非结构参数(正则化参数)。

所以，下面给出开头给出问题的解答

• 增加训练集: Fix High Variance
• 减少特征维度（从已有的特征中挑选出一部分）: Fix High Variance
• 增加新特征: Fix High Bias
• 增加多项式元素（比如将特征平方后叠加到原特征上，相当于增加了非线性的输入）: Fix High Bias
• 减小正则化参数的 λ 值: Fix High Bias
• 增大正则化参数的 λ 值: Fix High Variance

实例分析

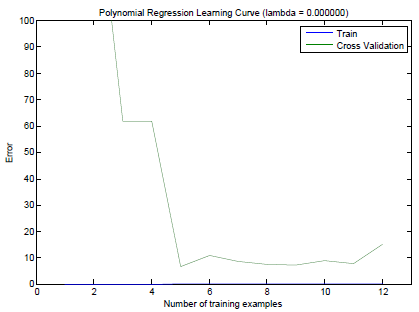
下图是未经调优模型的Learning Curve，训练模型用到的Feature是1维的。

可见训练集误差曲线变动较大，随着训练集数量m的增加还一直增加，误差较大。且训练集误差接近验证集误差。这说明模型处于High Bias的状态。所以我们将一维的Feature做乘方后扩充到8维，得出的Learning Curve见下图。

此时训练集误差随着m增加都维持在一个较小的范围，且验证集误差也随着m的增加而下降，训练集误差与验证集误差都较小，这就说明通过添加多项式特征，将模型的High Bias状态调整到了Just Right状态。此时模型的结构到达了正常状态。

将模型结构调整正确后，接下来再为模型调整正则化参数 λ 的值。