R语言与机器学习学习笔记(分类算法)(2)决策树算法
算法二:决策树算法
决策树定义
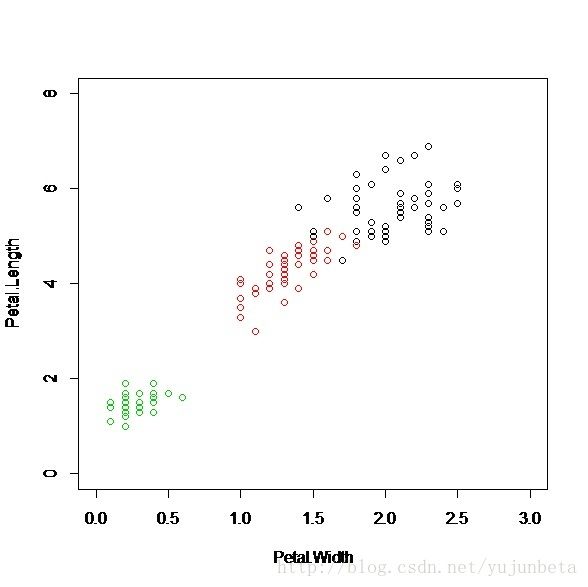
首先,我们来谈谈什么是决策树。我们还是以鸢尾花为例子来说明这个问题。
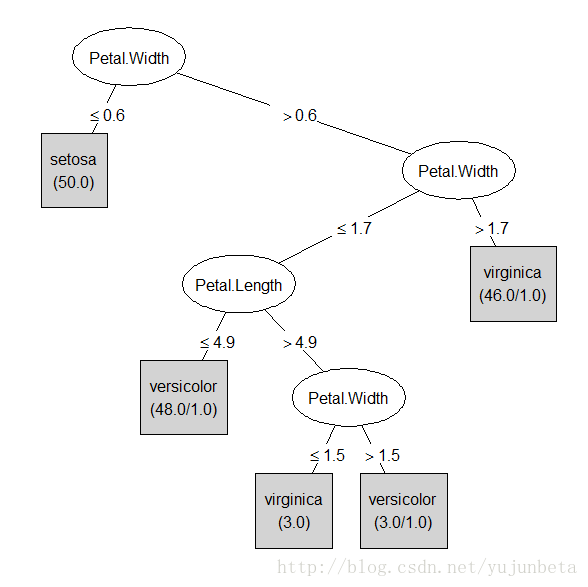
观察上图,我们判决鸢尾花的思考过程可以这么来描述:花瓣的长度小于2.4cm的是setosa(图中绿色的分类),长度大于1cm的呢?我们通过宽度来判别,宽度小于1.8cm的是versicolor(图中红色的分类),其余的就是virginica(图中黑色的分类)
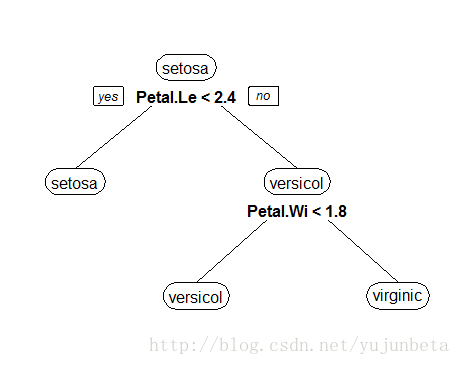
我们用图形来形象的展示我们的思考过程便得到了这么一棵决策树:
这种从数据产生决策树的机器学习技术叫做决策树学习, 通俗点说就是决策树,说白了,这是一种依托于分类、训练上的预测树,根据已知预测、归类未来。
前面我们介绍的k-近邻算法也可以完成很多分类任务,但是他的缺点就是含义不清,说不清数据的内在逻辑,而决策树则很好地解决了这个问题,他十分好理解。从存储的角度来说,决策树解放了存储训练集的空间,毕竟与一棵树的存储空间相比,训练集的存储需求空间太大了。
决策树的构建
一、KD3的想法与实现
下面我们就要来解决一个很重要的问题:如何构造一棵决策树?这涉及十分有趣的细节。
先说说构造的基本步骤,一般来说,决策树的构造主要由两个阶段组成:第一阶段,生成树阶段。选取部分受训数据建立决策树,决策树是按广度优先建立直到每个叶节点包括相同的类标记为止。第二阶段,决策树修剪阶段。用剩余数据检验决策树,如果所建立的决策树不能正确回答所研究的问题,我们要对决策树进行修剪直到建立一棵正确的决策树。这样在决策树每个内部节点处进行属性值的比较,在叶节点得到结论。从根节点到叶节点的一条路径就对应着一条规则,整棵决策树就对应着一组表达式规则。
问题:我们如何确定起决定作用的划分变量。
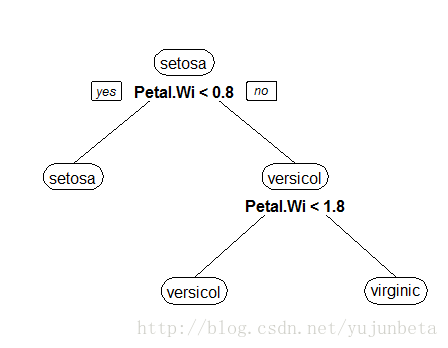
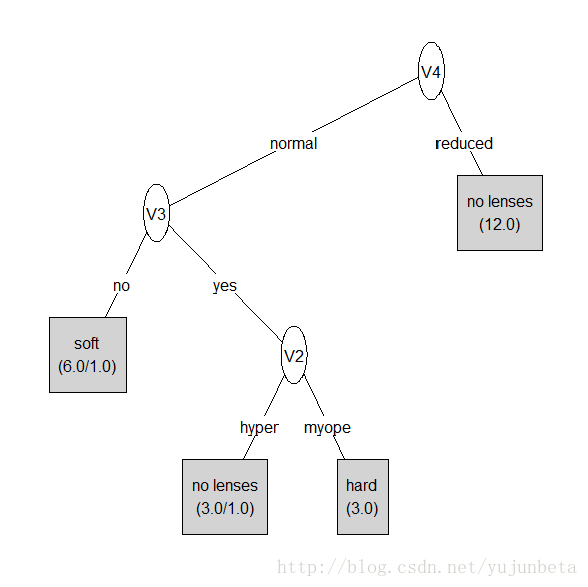
我还是用鸢尾花的例子来说这个问题思考的必要性。使用不同的思考方式,我们不难发现下面的决策树也是可以把鸢尾花分成3类的。
为了找到决定性特征,划分出最佳结果,我们必须认真评估每个特征。通常划分的办法为信息增益和基尼不纯指数,对应的算法为C4.5和CART。
关于信息增益和熵的定义烦请参阅百度百科,这里不再赘述。
直接给出计算熵与信息增益的R代码:
1、 计算给定数据集的熵
calcent<-function(data){
nument<-length(data[,1])
key<-rep("a",nument)
for(i in 1:nument)
key[i]<-data[i,length(data)]
ent<-0
prob<-table(key)/nument
for(i in 1:length(prob))
ent=ent-prob[i]*log(prob[i],2)
return(ent)
}我们这里把最后一列作为衡量熵的指标,例如数据集mudat(自己定义的)
> mudat
x y z
1 1 1 y
2 1 1 y
3 1 0 n
4 0 1 n
5 0 1 n
计算熵
> calcent(mudat)
1
0.9709506
熵越高,混合的数据也越多。得到熵之后,我们就可以按照获取最大信息增益的方法划分数据集
2、 按照给定特征划分数据集
为了简单起见,我们仅考虑标称数据(对于非标称数据,我们采用划分的办法把它们化成标称的即可)。
R代码:
split<-function(data,variable,value){
result<-data.frame()
for(i in 1:length(data[,1])){
if(data[i,variable]==value)
result<-rbind(result,data[i,-variable])
}
return(result)
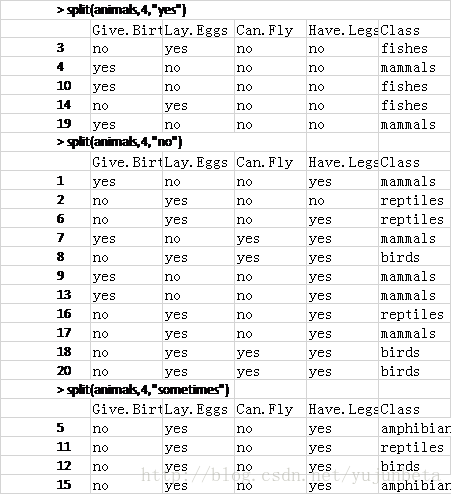
}这里要求输入的变量为:数据集,划分特征变量的序号,划分值。我们以前面定义的mudat为例,以“X”作为划分变量,划分得到的数据集为:
> split(mudat,1,1)
y z
1 1 y
2 1 y
3 0 n
> split(mudat,1,0)
y z
4 1 n
5 1 n
3、选择最佳划分(基于熵增益)
choose<-function(data){
numvariable<-length(data[1,])-1
baseent<-calcent(data)
bestinfogain<-0
bestvariable<-0
infogain<-0
featlist<-c()
uniquevals<-c()
for(i in1:numvariable){
featlist<-data[,i]
uniquevals<-unique(featlist)
newent<-0
for(jin 1:length(uniquevals)){
subset<-split(data,i,uniquevals[j])
prob<-length(subset[,1])/length(data[,1])
newent<-newent+prob*calcent(subset)
}
infogain<-baseent-newent
if(infogain>bestinfogain){
bestinfogain<-infogain
bestvariable<-i
}
}
return(bestvariable)
}函数choose包含三个部分,第一部分:求出一个分类的各种标签;第二部分:计算每一次划分的信息熵;第三部分:计算最好的信息增益,并返回分类编号。
我们以上面的简易例子mudat为例,计算划分,有:
> choose(mudat)
[1] 1
也就是告诉我们,将第一个变量值为1的分一类,变量值为0的分为另一类,得到的划分是最好的。
4、 递归构建决策树
我们以脊椎动物数据集为例,这个例子来自《数据挖掘导论》,具体数据集已上传至百度云盘(点击可下载)
我们先忽略建树细节,由于数据变量并不大,我们手动建一棵树先。
>animals<-read.csv("D:/R/data/animals.csv")
>choose(animals)
[1] 1
这里变量1代表names,当然是一个很好的分类,但是意义就不大了,我们暂时的解决方案是删掉名字这一栏,继续做有:
>choose(animals)
[1] 4
我们继续重复这个步骤,直至choose分类为0或者没办法分类(比如sometimes live in water的动物)为止。得到最终分类树。
给出分类逻辑图(遵循多数投票法):
至于最后的建树画图涉及R的绘图包ggplot,这里不再给出细节。
下面我们使用著名数据集——隐形眼镜数据集,利用上述的想法实现一下决策树预测隐形眼镜类型。这个例子来自《机器学习实战》,具体数据集已上传至百度云盘(点击可下载)。
下面是一个十分简陋的建树程序(用R实现的),为了叙述方便,我们给隐形眼镜数据名称加上标称:age,prescript,astigmatic,tear rate.
建树的R程序简要给出如下:
bulidtree<-function(data){
if(choose(data)==0)
print("finish")
else{
print(choose(data))
level<-unique(data[,choose(data)])
if(level==1)
print("finish")
else
for(i in1:length(level)){
data1<-split(data,choose(data),level[i])
if(length(data1)==1)print("finish")
else
bulidtree(data1)
}
}
}运行结果:
>bulidtree(lenses)
[1] 4
[1]"finish"
[1] 3
[1] 1
[1]"finish"
[1]"finish"
[1] 1
[1]"finish"
[1]"finish"
[1] 2
[1]"finish"
[1] 1
[1]"finish"
[1]"finish"
[1]"finish"
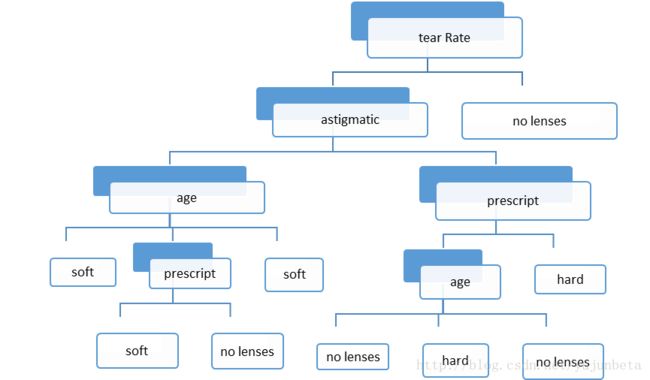
这棵树的解读有些麻烦,因为我们没有打印标签,(程序的简陋总会带来这样,那样的问题,欢迎帮忙完善),人工解读一下:
首先利用4(tear rate)的特征reduce,normal将数据集划分为nolenses(至此完全分类),normal的情况下,根据3(astigmatic)的特征no,yes分数据集(划分顺序与因子在数据表的出现顺序有关),no这条分支上选择1(age)的特征pre,young,presbyopic划分,前两个得到结果soft,最后一个利用剩下的一个特征划分完结(这里,由于split函数每次调用时,都删掉了一个特征,所以这里的1是实际第二个变量,这个在删除变量是靠前的情形时要注意),yes这条分支使用第2个变量prescript作为特征划分my ope划分完结,hyper利用age进一步划分,得到最终分类。
画图说明逻辑:
这里并没有进行剪枝,可能出现过拟合情形,我们暂不考虑剪枝的问题,下面的问题我想是更加迫切需要解决的:在选择根节点和各内部节点中的分支属性时,采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息。那么如何处理这些问题,C4.5算法不失为一个较好的解决方案。
二、C4.5算法
C4.5算法描述 :
(1) 创建根节点N;
(2) IF T都属于同一类C,则返回N为叶节点,标记为类C;
(3) IF T_attributelist为空或T中所剩的样本数少于某给定值则返回N为叶节点,标记为T中出现最多的类;
(4) FOR each T_attributelist中的属性计算信息增益率information gain ratio;
(5) N的测试属性test_attribute=T_attributelist中具有最高信息增益率的属性;
(6) IF测试属性为连续型则找到该属性的分割阀值;
(7) FOR each 由节点N长出的新叶节点{
IF 该叶节点对应的样本子集T’为空
则分裂该叶节点生成一个新叶节点,将其标记为T中出现最多的类;
ELSE在该叶节点上执行C4.5formtree(T’,T’_attributelist),对它继续分裂;
}
(8) 计算每个节点的分类错误,进行树剪枝。
以鸢尾花数据为例子,使用C4.5算法得到的分类树见下图:
预测结果:
观察\预测 setosa versicolor virginica
setosa 50 0 0
versicolor 0 49 1
virginica 0 2 48
下面我们使用上面提到的隐形眼镜数据集,利用C4.5实现一下决策树预测隐形眼镜类型。
得到结果:
hard no lenses soft
hard 3 1 0
no lenses 0 14 1
soft 0 0 5
看起来还不错,不是吗?
(注:图片与预测表输出结果是已经经过剪枝的,所以可能和我们之前程序算出的有些不同)
这里我们再次实现一下脊椎动物数据集的例子(使用C4.5),得到的分类逻辑图(R的直接输出结果):
Give.Birth = no
| Live.in.Water = no
| | Can.Fly = no: reptiles (4.0/1.0)
| | Can.Fly = yes: birds (3.0)
| Live.in.Water = sometimes: amphibians (4.0/2.0)
| Live.in.Water = yes: fishes (2.0)
Give.Birth = yes: mammals (7.0/1.0)
这个分类与我们之前使用ID3分类得到的结果有所不同(搜索效率高了一些,准确率相当),使用信息增益倾向于多分类的贪心算法导致的不足在这里显示的淋漓尽致,更可以看出C4.5比ID3改进的地方绝不止能处理连续变量这一条。
三、 CART算法
CART算法描述
(1) 创建根节点N;
(2) 为N分配类别;
(3) IF T都属于同一类别OR T中只剩一个样本
则返回N为叶节点,为其分配类别;
(4) FOR each T_attributelist 中的属性
执行该属性上的一个划分,计算此次划分的GINI系数;
(5) N的测试属性test_attribute=T_attributelist中具有最小GINI系数的属性;
(6) 划分T得T1、T2两个子集;
(7) 调用cartformtree(T1);
(8) 调用cartformtree(T2);
以鸢尾花数据集为例,使用cart算法,得到决策树:
要实现C4.5算法,R提供了一个程序包RWeka,J48函数可以实现决策树的构建,至于cart算法,R中的tree包提供函数tree来实现决策树的构建。下面我们来简要介绍他们:
J48(formula, data, subset, na.action,
control = Weka_control(), options = NULL)
tree(formula, data, weights, subset,
na.action = na.pass, control = tree.control(nobs, ...),
method = "recursive.partition",
split = c("deviance", "gini"),
model = FALSE, x = FALSE, y = TRUE, wts = TRUE, ...)
split为划分指标,分为deviance(偏差)和”gini”(基尼)
control涉及树剪枝的各种凶残细节,有兴趣的可以通过阅读帮助文档解决。而且剪枝是一个十分复杂的过程,剪枝也是视需求而定的,C4.5是事后剪枝,id3也就是我们试图实现的建树,也可以去手动剪枝。
四、R内置命令实现
我们之前的C4.5的建树R代码如下:
鸢尾花一例:
library(RWeka)
library(party)
oldpar=par(mar=c(3,3,1.5,1),mgp=c(1.5,0.5,0),cex=0.3)
data(iris)
m1<-J48(Species~Petal.Width+Petal.Length,data=iris)
m1
table(iris$Species,predict(m1))
write_to_dot(m1)
if(require("party",quietly=TRUE))
plot(m1)隐形眼镜一例:
lenses<-read.csv("D:/R/data/lenses.csv",head=FALSE)
m1<-J48(V5~.,data=lenses)
m1
table(lenses$V5,predict(m1))
write_to_dot(m1)
if(require("party",quietly=TRUE))
plot(m1)CART算法的鸢尾花例:
library(tree)
oldpar=par(mar=c(3,3,1.5,1),mgp=c(1.5,0.5,0),cex=1.2)
ir.tr <- tree(Species~Petal.Width+Petal.Length, iris)
ir.tr
plot(ir.tr)
text(ir.tr)对于决策树的构建,R中个人用的比较多的是函数包rpart中的函数rpart与prune。具体介绍在之前的博文《R语言与机器学习中的回归方法学习笔记》中有提及,这里不再赘述。
决策树是一个弱分类器,我们从脊椎动物数据集就可以看到,没有办法完全分类,这时将弱学习器组合在一起的,根据多数投票法得到的强学习器是你可以进一步关注的,ada boost,bagging,random forest,这些内容你都可以了解一些(这些上一篇文章《R语言与机器学习中的回归方法学习笔记》有所涉猎,但也未详述)。
Further Reading:
关于C4.5的内容可以参阅yfx416的《C4.5决策树》
关于随机森林等内容可以参阅LeftNotEasy的《决策树模型组合之随机森林与GBDT》
关于学习器组合的内容可以参阅LeftNotEasy的《模型组合之Boosting与Gradient Boosting》
预告
- 算法三:朴素贝叶斯算法
- 算法四:支持向量机
- 算法五:神经网络
- 算法六:logistic回归
(to be continue)