R语言与函数估计学习笔记（核方法与局部多项式）

非参数方法

用于函数估计的非参数方法大致上有三种：核方法、局部多项式方法、样条方法。
非参的函数估计的优点在于稳健，对模型没有什么特定的假设，只是认为函数光滑，避免了模型选择带来的风险；但是，表达式复杂，难以解释，计算量大是非参的一个很大的毛病。所以说使用非参有风险，选择需谨慎。
非参的想法很简单：函数在观测到的点取观测值的概率较大，用x附近的值通过加权平均的办法估计函数\( f(x) \)的值。

核方法

当加权的权重是某一函数的核（关于“核”的说法可参见之前的博文《R语言与非参数统计（核密度估计）》）,这种方法就是核方法，常见的有Nadaraya-Watson核估计与Gasser-Muller核估计方法，也就是很多教材里谈到的NW核估计与GM核估计，这里我们还是不谈核的选择，将一切的核估计都默认用Gauss核处理。
NW核估计形式为：\[ \hat f_h(x)=\frac{\sum_{i=1}^n K_h(x_i-x)y_i}{\sum_{i=1}^n K_h(x_i-x)} \]GM核估计形式为：\[ \hat f_h(x)=\sum_{i=1}^n y_i \int_{s_{i-1}}^{s_i} K_h(u-x)du \]式中\( s_i=(x_i+x_{i+1})/2,x_0=-\infty,x_{n+1}=\infty \)。

x <- seq(-1, 1, length = 20)
y <- 5 * x * cos(5 * pi * x)
h <- 0.088
fx.hat <- function(z, h) {
    dnorm((z - x)/h)/h
}
KSMOOTH <- function(h, y, x) {
    n <- length(y)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        a <- fx.hat(x[i], h)
        s.hat[i] <- sum(y * a/sum(a))
    }
    return(s.hat)
}

ksmooth.val <- KSMOOTH(h, y, x)

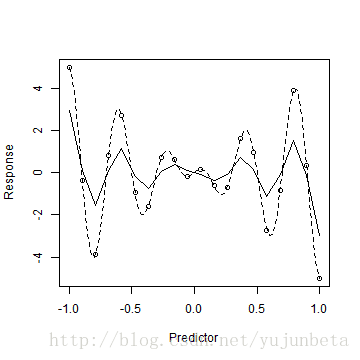
plot(x, y, xlab = "Predictor", ylab = "Response")
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5), lty = 2, add = T)
lines(x, ksmooth.val, type = "l")

可以看出，核方法基本估计出了函数的形状，但是效果不太好，这个是由于样本点过少导致的，我们可以将样本容量扩大一倍，看看效果：

x <- seq(-1, 1, length = 40)
y <- 5 * x * cos(5 * pi * x)
h <- 0.055
fx.hat <- function(z, h) {
    dnorm((z - x)/h)/h
}
NWSMOOTH <- function(h, y, x) {
    n <- length(y)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        a <- fx.hat(x[i], h)
        s.hat[i] <- sum(y * a/sum(a))
    }
    return(s.hat)
}

NWsmooth.val <- NWSMOOTH(h, y, x)

plot(x, y, xlab = "Predictor", ylab = "Response", col = 1)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5), lty = 1, add = T, col = 1)
lines(x, NWsmooth.val, lty = 2, col = 2)
A <- data.frame(x = seq(-1, 1, length = 1000))
model.linear <- lm(y ~ poly(x, 9))
lines(seq(-1, 1, length = 1000), predict(model.linear, A), lty = 3, col = 3)
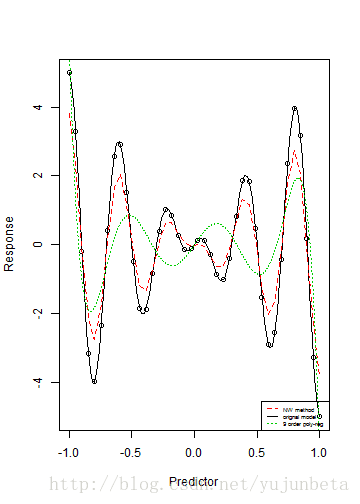
letters <- c("NW method", "orignal model", "9 order poly-reg")
legend("bottomright", legend = letters, lty = c(2, 1, 3), col = c(2, 1, 3), 
    cex = 0.5)

可以看到估计效果还是很好的，至少比基函数的办法要好一些。那么我们来看看GM核方法：

x <- seq(-1, 1, length = 40)
y <- 5 * x * cos(5 * pi * x)
h <- 0.055

GMSMOOTH <- function(y, x, h) {
    n <- length(y)
    s <- c(-Inf, 0.5 * (x[-n] + x[-1]), Inf)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        fx.hat <- function(z, h, x) {
            dnorm((x - z)/h)/h
        }
        a <- y[i] * integrate(fx.hat, s[i], s[i + 1], h = h, x = x[i])$value
        s.hat[i] <- sum(a)
    }
    return(s.hat)
}

GMsmooth.val <- GMSMOOTH(y, x, h)

plot(x, y, xlab = "Predictor", ylab = "Response", col = 1)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5), lty = 1, add = T, col = 1)
lines(x, GMsmooth.val, lty = 2, col = 2)
A <- data.frame(x = seq(-1, 1, length = 1000))
model.linear <- lm(y ~ poly(x, 9))
lines(seq(-1, 1, length = 1000), predict(model.linear, A), lty = 3, col = 3)
letters <- c("GM method", "orignal model", "9 order poly-reg")
legend("bottomright", legend = letters, lty = c(2, 1, 3), col = c(2, 1, 3), 
    cex = 0.5)

我们来看看两个核估计办法的差异：

x <- seq(-1, 1, length = 40)
y <- 5 * x * cos(5 * pi * x)
h <- 0.055
fx.hat <- function(z, h) {
    dnorm((z - x)/h)/h
}
NWSMOOTH <- function(h, y, x) {
    n <- length(y)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        a <- fx.hat(x[i], h)
        s.hat[i] <- sum(y * a/sum(a))
    }
    return(s.hat)
}

NWsmooth.val <- NWSMOOTH(h, y, x)

GMSMOOTH <- function(y, x, h) {
    n <- length(y)
    s <- c(-Inf, 0.5 * (x[-n] + x[-1]), Inf)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        fx.hat <- function(z, h, x) {
            dnorm((x - z)/h)/h
        }
        a <- y[i] * integrate(fx.hat, s[i], s[i + 1], h = h, x = x[i])$value
        s.hat[i] <- sum(a)
    }
    return(s.hat)
}

GMsmooth.val <- GMSMOOTH(y, x, h)

plot(x, y, xlab = "Predictor", ylab = "Response", col = 1)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5), lty = 1, add = T, col = 1)
lines(x, NWsmooth.val, lty = 2, col = 2)
lines(x, GMsmooth.val, lty = 3, col = 3)
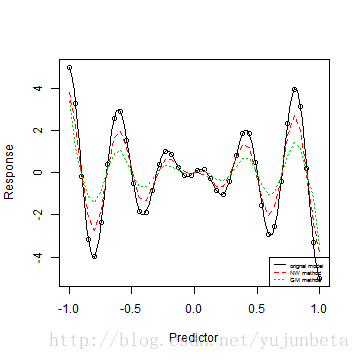
letters <- c("orignal model", "NW method", "GM method")
legend("bottomright", legend = letters, lty = 1:3, col = 1:3, cex = 0.5)

从图中可以看到NW估计的方差似乎小些，事实也确实如此，GM估计的渐进方差约为NW估计的1.5倍。但是GM估计解决了一些计算的难题。
我们最后还是来展示不同窗宽的选择对估计的影响（这里以NW估计为例）：

x <- seq(-1, 1, length = 40)
y <- 5 * x * cos(5 * pi * x)
fx.hat <- function(z, h) {
    dnorm((z - x)/h)/h
}
NWSMOOTH <- function(h, y, x) {
    n <- length(y)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        a <- fx.hat(x[i], h)
        s.hat[i] <- sum(y * a/sum(a))
    }
    return(s.hat)
}

h <- 0.025
NWsmooth.val0 <- NWSMOOTH(h, y, x)
h <- 0.05
NWsmooth.val1 <- NWSMOOTH(h, y, x)
h <- 0.1
NWsmooth.val2 <- NWSMOOTH(h, y, x)
h <- 0.2
NWsmooth.val3 <- NWSMOOTH(h, y, x)
h <- 0.3
NWsmooth.val4 <- NWSMOOTH(h, y, x)

plot(x, y, xlab = "Predictor", ylab = "Response", col = 1)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5), lty = 1, add = T, col = 1)
lines(x, NWsmooth.val0, lty = 2, col = 2)
lines(x, NWsmooth.val1, lty = 3, col = 3)
lines(x, NWsmooth.val2, lty = 4, col = 4)
lines(x, NWsmooth.val3, lty = 5, col = 5)
lines(x, NWsmooth.val4, lty = 6, col = 6)
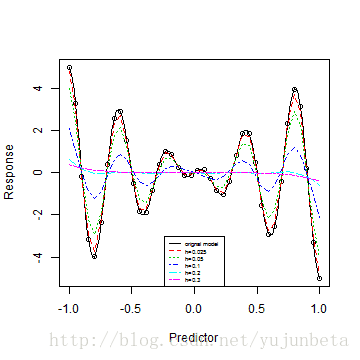
letters <- c("orignal model", "h=0.025", "h=0.05", "h=0.1", "h=0.2", "h=0.3")
legend("bottom", legend = letters, lty = 1:6, col = 1:6, cex = 0.5)

可以看到窗宽越大，估计越光滑，误差越大，窗宽越小，估计越不光滑，但拟合优度有提高，却也容易过拟合。
窗宽怎么选，一个可行的办法就是CV，通俗的讲就是取一个观测做测试集，剩下的做训练集，看NMSE。R代码如下：

x <- seq(-1, 1, length = 40)
y <- 5 * x * cos(5 * pi * x)
# h<-0.055
NWSMOOTH <- function(h, y, x, z) {
    n <- length(y)
    s.hat <- rep(0, n)
    s.hat1 <- rep(0, n)
    for (i in 1:n) {
        s.hat[i] <- dnorm((x[i] - z)/h)/h * y[i]
        s.hat1[i] <- dnorm((x[i] - z)/h)/h
    }
    z.hat <- sum(s.hat)/sum(s.hat1)
    return(z.hat)
}
CVRSS <- function(h, y, x) {
    cv <- NULL
    for (i in seq(x)) {
        cv[i] <- (y[i] - NWSMOOTH(h, y[-i], x[-i], x[i]))^2
    }
    mean(cv)
}
h <- seq(0.01, 0.2, by = 0.005)
cvrss.val <- rep(0, length(h))
for (i in seq(h)) {
    cvrss.val[i] <- CVRSS(h[i], y, x)
}

plot(h, cvrss.val, type = "b")

从图中我们可以见到CV值在0.01到0.05的变化都不大，这时，我们应该选择较大的h，使得函数较为光滑，但是0.05后，cv变化较大，说明我们选择窗宽也不能过大，否则也会出毛病的。那么是不是h越小越好呢？虽然上面一个例子给了我们这样一个错觉，我们下面这个例子就可以打破它，数据来自《computational statistics》一书的essay data一例。

easy <- read.table("D:/R/data/easysmooth.dat", header = T)
x <- easy$X
y <- easy$Y
NWSMOOTH <- function(h, y, x, z) {
    n <- length(y)
    s.hat <- rep(0, n)
    s.hat1 <- rep(0, n)
    for (i in 1:n) {
        s.hat[i] <- dnorm((x[i] - z)/h)/h * y[i]
        s.hat1[i] <- dnorm((x[i] - z)/h)/h
    }
    z.hat <- sum(s.hat)/sum(s.hat1)
    return(z.hat)
}
CVRSS <- function(h, y, x) {
    cv <- NULL
    for (i in seq(x)) {
        cv[i] <- (y[i] - NWSMOOTH(h, y[-i], x[-i], x[i]))^2
    }
    mean(cv)
}
h <- seq(0.01, 0.3, by = 0.02)
cvrss.val <- rep(0, length(h))
for (i in seq(h)) {
    cvrss.val[i] <- CVRSS(h[i], y, x)
}

plot(h, cvrss.val, type = "b")

从上图就可以看到，最佳窗宽约为0.15，而不是0.01.
和树回归类似，我们的核方法就是提供了一个常数来渐进这个函数，我们这里仍然可以考虑模型树的想法，用一阶或者高阶多项式来作加权估计，这就有了局部多项式估计。

局部多项式

估计的想法是认为未知函数\( f(x) \)在近邻邻域内可由某一多项式近似（这是Taylor公式的结果），在\( x_0 \)的邻域内最小化：\[ arg \underset{\beta_0,\cdots,\beta_p}{min}\sum_{i=1}^n[y_i-\sum_{j=0}^p \beta_j(x_i-x_0)^j]^2 K_h(x_i-x_0) \]具体做法为：
（1）对于每个xi，以该点为中心，计算出对应点处的权重\( K_h(x_i-x) \)；

（2）采用加权最小二乘法（WLS）估计其参数，并用得到的模型估计该结点对应的x值对应y值，作为y|xi的估计值（只要这一个点的估计值）；

（3）估计下一个点xj；

（4）将每个y|xi的估计值连接起来。
我们这里以《computational statistics》一书的essay data为例来说明局部多项式估计

easy <- read.table("D:/R/data/easysmooth.dat", header = T)
x <- easy$X
y <- easy$Y
h <- 0.16

## FUNCTIONS USES HAT MATRIX

LPRSMOOTH <- function(y, x, h) {
    n <- length(y)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        weight <- dnorm((x - x[i])/h)
        mod <- lm(y ~ x, weights = weight)
        s.hat[i] <- as.numeric(predict(mod, data.frame(x = x[i])))
    }
    return(s.hat)
}

lprsmooth.val <- LPRSMOOTH(y, x, h)

s <- function(x) {
    (x^3) * sin((x + 3.4)/2)
}
x.plot <- seq(min(x), max(x), length.out = 1000)
y.plot <- s(x.plot)
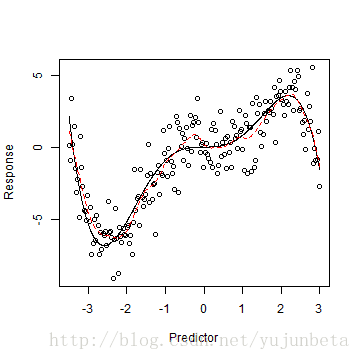
plot(x, y, xlab = "Predictor", ylab = "Response")
lines(x.plot, y.plot, lty = 1, col = 1)
lines(x, lprsmooth.val, lty = 2, col = 2)

我们回到最开始我们提到的三角函数的例子，我们可以看到：

x <- seq(-1, 1, length = 40)
y <- 5 * x * cos(5 * pi * x)

## FUNCTIONS


LPRSMOOTH <- function(y, x, h) {
    n <- length(y)
    s.hat <- rep(0, n)
    for (i in 1:n) {
        weight <- dnorm((x - x[i])/h)
        mod <- lm(y ~ x, weights = weight)
        s.hat[i] <- as.numeric(predict(mod, data.frame(x = x[i])))
    }
    return(s.hat)
}


h <- 0.15
lprsmooth.val1 <- LPRSMOOTH(y, x, h)


h <- 0.066
lprsmooth.val2 <- LPRSMOOTH(y, x, h)

plot(x, y, xlab = "Predictor", ylab = "Response")
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5), lty = 1, add = T, col = 1)
lines(x, lprsmooth.val1, lty = 2, col = 2)
lines(x, lprsmooth.val2, lty = 3, col = 3)
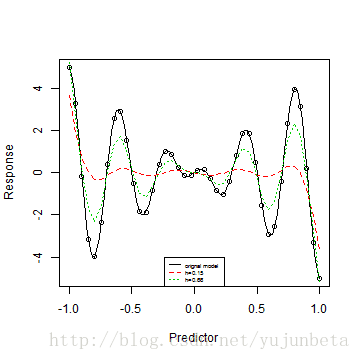
letters <- c("orignal model", "h=0.15", "h=0.66")
legend("bottom", legend = letters, lty = 1:3, col = 1:3, cex = 0.5)

R中提供了很多的函数包来做非参数回归，常用的有：KernSmooth包的函数locpoly()，locpol的locpol()，locCteSmootherC()以及locfit的locfit().具体的参数设置较为简单，这里就不多说了。我们以开篇的三角函数模型的例子为例来看看如何使用它们：

library(KernSmooth)  #函数locpoly()
library(locpol)  #locpol(); locCteSmootherC()
library(locfit)  #locfit()

x <- seq(-1, 1, length = 40)
y <- 5 * x * cos(5 * pi * x)

f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1)
points(x, y)

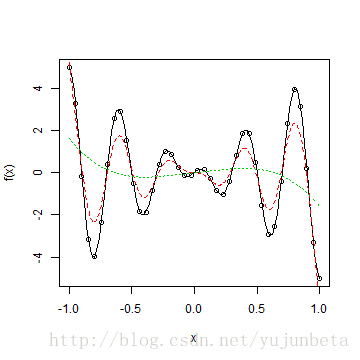
fit <- locpoly(x, y, bandwidth = 0.066)
lines(fit, lty = 2, col = 2)

d <- data.frame(x = x, y = y)
r <- locfit(y ~ x, d)  #一般来说，locfit函数自动选的窗宽偏大，函数较光滑
lines(r, lty = 3, col = 3)

xeval <- seq(-1, 1, length = 10)
cuest <- locCuadSmootherC(d$x, d$y, xeval, 0.066, gaussK)
cuest

##          x   beta0   beta1   beta2     den
## 1  -1.0000  5.0858 -35.152 -222.58 0.07571
## 2  -0.7778 -3.3233  11.966  514.42 4.22454
## 3  -0.5556  1.9804 -16.219 -279.47 4.26349
## 4  -0.3333 -0.8416  13.137   83.37 4.26349
## 5  -0.1111  0.1924  -4.983   27.90 4.26349
## 6   0.1111 -0.1924  -4.983  -27.90 4.26349
## 7   0.3333  0.8416  13.137  -83.37 4.26349
## 8   0.5556 -1.9804 -16.219  279.47 4.26349
## 9   0.7778  3.3233  11.966 -514.42 4.22454
## 10  1.0000 -5.0858 -35.152  222.58 0.07571

关于局部多项式估计的想法还有很多，比如我们只考虑近邻的数据作最小二乘估计，再比如我们可以修改权重，使得我们的窗宽与近邻点的距离有关，再比如，我们可以考虑不采用最小二乘做优化，而是对最小二乘加上一点点的惩罚……我们将第一个想法称之为running line，第二个想法称之为loess,第三个想法依据你的惩罚方式不同有不同的说法。我们将running line的R程序给出如下：

RLSMOOTH <- function(k, y, x) {
    n <- length(y)
    s.hat <- rep(0, n)
    b <- (k - 1)/2
    if (k > 1) {
        for (i in 1:(b + 1)) {
            xi <- x[1:(b + i)]
            xi <- cbind(rep(1, length(xi)), xi)
            hi <- xi %*% solve(t(xi) %*% xi) %*% t(xi)
            s.hat[i] <- y[1:(b + i)] %*% hi[i, ]

            xi <- x[(n - b - i + 1):n]
            xi <- cbind(rep(1, length(xi)), xi)
            hi <- xi %*% solve(t(xi) %*% xi) %*% t(xi)
            s.hat[n - i + 1] <- y[(n - b - i + 1):n] %*% hi[nrow(hi) - i + 1, 
                ]
        }
        for (i in (b + 2):(n - b - 1)) {
            xi <- x[(i - b):(i + b)]
            xi <- cbind(rep(1, length(xi)), xi)
            hi <- xi %*% solve(t(xi) %*% xi) %*% t(xi)
            s.hat[i] <- y[(i - b):(i + b)] %*% hi[b + 1, ]
        }
    }
    if (k == 1) {
        s.hat <- y
    }
    return(s.hat)
}

我们也一样可以对running line做局部多项式回归，代码如下：

WRLSMOOTH <- function(k, y, x, h) {
    n <- length(y)
    s.hat <- rep(0, n)
    b <- (k - 1)/2
    if (k > 1) {
        for (i in 1:(b + 1)) {
            xi <- x[1:(b + i)]
            xi <- cbind(rep(1, length(xi)), xi)
            hi <- xi %*% solve(t(xi) %*% xi) %*% t(xi)
            s.hat[i] <- y[1:(b + i)] %*% hi[i, ]

            xi <- x[(n - b - i + 1):n]
            xi <- cbind(rep(1, length(xi)), xi)
            hi <- xi %*% solve(t(xi) %*% xi) %*% t(xi)
            s.hat[n - i + 1] <- y[(n - b - i + 1):n] %*% hi[nrow(hi) - i + 1, 
                ]
        }
        for (i in (b + 2):(n - b - 1)) {
            xi <- x[(i - b):(i + b)]
            weight <- dnorm((xi - x[i])/h)
            mod <- lm(y[(i - b):(i + b)] ~ xi, weights = weight)
            s.hat[i] <- as.numeric(predict(mod, data.frame(xi = x[i])))
        }
    }
    if (k == 1) {
        s.hat <- y
    }
    return(s.hat)
}

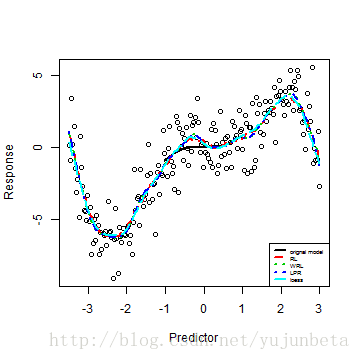
R中也提供了函数lowess()来做loess回归。我们这里不妨以essay data为例，看看这三个估计有多大的差别：

本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。