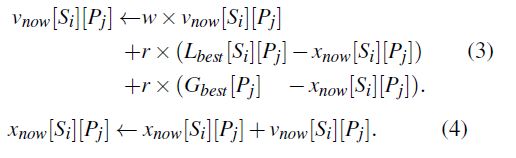MOPT: Optimize Mutation Scheduling for Fuzzers
目录
摘要
1.简介
2 Background
2.1 Mutation-based Fuzzing
2.2突变算子
2.3突变调度方案
2.4突变效率
3.Overview of MOPT
3.1 Design Philosophy
3.2 Particle Swarm Optimization (PSO)
3.3设计细节
3.3.1Particles
3.3.2 Local Best Position Lbest
3.3.3 Global Best Position Gbest
3.3.4 Multiple Swarms
4 Implementation of MOPT
4.1 MOPT Main Framework
4.1.1 PSO Initialization Module
4.1.2 Pilot Fuzzing Module
4.1.3 Core Fuzzing Module
4.1.4 PSO Updating Module
4.2 Pacemaker Fuzzing Mode
8 Related Work
摘要
基于变异的模糊测试是目前最流行的漏洞发现方法之一。其生成有趣测试用例的性能很大程度上取决于变异调度策略。然而,现有的模糊测试通常遵循一个特定的(例如,统一的)分布来选择变异算子,这在寻找通用程序上的漏洞方面效率很低。因此,本文提出了一种新的突变调度方案MOPT,使基于突变的模糊测试更有效地发现漏洞。MOPT采用一种定制的粒子群优化算法(PSO),从模糊有效性的角度寻找算子的最优选择概率分布,并提供一种引领模糊测试模式,以加快PSO的收敛速度。我们将MOPT应用于最先进的模糊测试工具AFL、AFLFAST和Vuzzer,分别实现了MOPT-AFL、-AFLFAST和-Vuzzer,并在13个真实的开源程序上进行了评估。结果表明,MOPT-AFL发现的安全漏洞比AFL多170%,崩溃率比AFL高350%。MOPT AFLFAST和MOPT Vuzzer的表现也优于其对手。此外,广泛的评价也表明,MOPT具有良好的合理性、兼容性和稳定性,同时引入了可忽略不计的成本。
1.简介
基于突变的模糊测试是最普遍的漏洞发现解决方案之一。一般来说,它获取种子测试用例并按一定顺序选择它们,然后以各种方式对它们进行变异,并使用新生成的测试用例测试目标程序。在过去的几年中,已经提出了许多新的解决方案,包括改进种子生成解决方案的解决方案[1、2、3、4]、改进种子选择策略的解决方案[5、6、7、8、9]、提高测试速度和代码覆盖率的解决方案[10、11、12、13]以及将其他技术与模糊测试技术相结合的解决方案[14、15、16]。
然而,如何通过改变测试用例来生成新的有效的测试用例却很少受到关注。大量公认的模糊测试工具,如AFL[17]及其后代Libfuzzer[18]、Honggfuzz[19]、BFF[2]和Vuzzer[7],通常预先定义一组突变操作符,以描述突变的位置(如哪个字节)和如何突变(如添加、删除或替换字节)。在模糊测试过程中,他们使用特定的突变调度程序从这个预先定义的集合中选择操作符,以使模糊测试用例发生突变并生成新的模糊测试用例。突变调度程序不是直接生成一个突变操作符,而是生成一个预先定义的操作符的概率分布,而模糊测试工具将根据这个分布选择操作符。例如,AFL统一选择突变运算符。
目前只有有限的解决方案专注于改进突变调度程序。以前的工作[8,9]利用强化学习动态地选择每一轮的突变算子。但是,它们在漏洞发现方面没有显示出显著的性能改进[8,9]。因此,需要一个更好的突变调度器。我们发现,大多数前人的工作都不能达到最佳性能,因为它们没有考虑到以下问题。
不同运营商的效率不同。不同的突变操作人员在寻找崩溃和路径上有不同的效率(如图3所示)。因此,选择具有均匀分布的变异算子的模糊测试可能会将不必要的计算能力花在效率低下的算子上,从而降低整体模糊测试效率。
一个操作员的效率随目标程序的不同而变化。每个操作员的效率都依赖于程序,并且不太可能或至少很难静态地推断出这种依赖性。因此,最优的突变调度器必须根据每个操作人员对目标程序的运行效率来决定每个程序。
一个操作员的效率随时间变化。在当前测试案例中表现良好的变异算子在极端情况下可能在以下测试案例中表现不佳。如前所述,最优变异调度程序依赖于算子的历史效率来计算最优概率分布来选择算子。由于操作效率的动态特性,这种概率计算过程应该收敛得很快。
调度程序会产生性能开销。突变调度对模糊测试的执行速度有影响。由于执行速度是影响模糊测试效率的关键因素之一,一个更好的变异调度程序应该减少计算量,以避免减慢模糊测试速度。
机器学习数据不平衡。在模糊测试过程中,正样本和负样本的数量不平衡,例如,一个变异算子只能以很小的概率生成有趣的测试用例,这可能会影响梯度下降算法和其他机器学习算法的有效性[8,9]。
本文将突变调度问题作为一个优化问题,提出了一种新的突变调度方案MOPT,旨在解决上述问题,提高模糊性能。MOPT以著名的优化算法粒子群优化(PSO)[20]为灵感,对候选变异算子的效率进行动态评估,并将其选择概率调整到最优分布。
mopt将每个突变算子建模为沿概率空间[xmin;xmax]移动的粒子,其中xmin和xmax分别是预先定义的最小和最大概率。在局部最佳概率和全局最佳概率的指导下,每一个粒子(即算子)都朝着其最佳选择概率移动,从而产生更高质量的测试用例。因此,MOPT的目标是通过对粒子发现的概率进行聚合,找到最优的算子选择概率分布,从而使聚合产生更高质量的测试用例。与PSO类似,MOPT根据粒子的局部最佳概率和全局最佳概率迭代更新每个粒子的概率。然后,将所有粒子的更新概率进行整合,得到一个新的概率分布。MOPT可以快速收敛到选择变异算子的概率分布的最佳解,从而显著提高模糊性能。
MOPT是一种通用方案,可以应用于各种基于突变的模糊测试。我们已将其应用于几种最先进的模糊测试,包括AFL[17]、AFLFAST[6]和Vuzzer[7],并分别实现了MOPT-AFL、-AFLFAST和-Vuzzer。在AFL及其衍生产品中,我们进一步设计了一种特殊的引领模糊测试方式,进一步加快了MOPT的收敛速度。
我们在13个现实世界项目中评估了这些原型。MOPT-AFL共发现112个安全漏洞,其中97个以前未知的漏洞(其中66个经CVE确认)和15个已知的CVE漏洞。与AFL相比,MOPT-AFL发现的漏洞多170%,崩溃多350%,程序路径多100%。MOPT AFLFAST和MOPT Vuzzer在我们的数据集上也超过了它们的对手。进一步论证了MOPT的合理性、稳定性和低成本性。
总之,我们做出了以下贡献:
- 我们调查了现有的突变调度程序的缺点,由此得出结论,突变操作人员应根据其历史表现进行调度。
- 提出了一种新的突变调度方案MOPT,能够选择更好的突变算子,实现更好的模糊测试效率。它可以广泛应用于现有的基于突变的模糊测试中。
- 我们将MOPT应用于几种最先进的模糊测试,包括AFL、AFLFAST和Vuzzer,并在13个现实世界项目中进行了评估。结果表明,MOPT能发现更多的漏洞、崩溃和程序路径,具有良好的稳定性、兼容性和低成本。
- MOPT-AFL发现了97个以前未知的安全漏洞,并帮助供应商提高其产品的安全性。它还发现这些程序(最新版本)中有15个以前已知的漏洞,这表明安全修补在实践中需要很长时间。我们也在https://github.com/puppet-meteor/mopt-afl上开放源代码MOPT-AFL以及使用的数据、种子集和结果,以促进这一领域的研究。
2 Background
2.1 Mutation-based Fuzzing
基于突变的模糊化[2,6,7,14,15,16,17,18,19]在不利用目标程序的先验知识(如测试用例规范)的情况下,发现漏洞。相反,它通过以某种方式对一些格式良好的种子测试用例进行变异来生成新的测试用例。
基于突变的模糊化的一般工作流程如下。fuzzer(1)维护一个种子测试用例队列,可以在运行时更新;(2)从队列中按一定顺序选择一些种子;(3)以各种方式变异种子;(4)使用新生成的测试用例测试目标程序,并报告漏洞或在必要时更新种子队列;然后(5)返回步骤(2)。
为了有效地引导变异和模糊测试,一些模糊测试工具还将在测试过程中使用目标程序来收集运行时信息,并用它来指导种子更新,决定选择哪种种子以及如何进行变异。本文主要研究突变阶段(即步骤(3))。
2.2突变算子
基于突变的模糊测试能以无数种方式使种子突变。考虑到性能和可用性,在实践中,这些模糊测试工具,包括AFL[17]及其后代,libfuzzer[18]、honggfuzz[19]、bff[2]和vuzzer[7]通常预先定义了一组突变算子,并选择其中一些在运行时对种子进行突变。这些变异操作符描述了变异的位置(例如,哪个字节)以及如何变异(例如,添加、删除或替换字节)。
例如,公认的模糊测试AFL预先定义了11种类型的突变算子,如表1所示。在每种类型中,都可能有几个具体的突变算子。例如,位翻转2/1运算符翻转2个连续位,其中跨步为1位。注意,不同的模糊测试可以定义不同的突变算子。
| 类型 | 说明 | 操作 |
| bitflip | 在测试用例中反转一个或多个连续的位,其中跨步是1位。 | bitflip 1/1 |
| byteflip | 在一个测试用例中反转一个或多个连续的字节,其中跨步是8位。 | bitflip 8/8 |
| arithmetic inc/dec | 对一个字节或几个连续字节执行加减运算。 | arith 8/8 |
| interesting values | 用硬编码的有趣值替换测试用例中的字节 | interest 8/8 |
| user extras | 使用用户提供的令牌覆盖或插入测试用例中的字节。 | user (over), user (insert) |
| auto extras | 在位翻转1/1期间,用AFL识别的标记覆盖测试用例中的字节。 | auto extras (over) |
| random bytes | 随机选择测试用例的一个字节并将该字节设置为随机值 | random byte |
| delete bytes | 随机选择几个连续的字节并删除它们 | delete bytes |
| insert bytes | 从一个测试用例中随机复制一些字节,并将它们插入到这个测试用例中的另一个位置。 | insert bytes |
| overwrite bytes | 在测试用例中随机覆盖几个连续的字节。 | overwrite bytes |
| crossover | 将两个不同测试用例中的两个部分拼接在一起,形成一个新的测试用例。 | crossover |
2.3突变调度方案
在运行时,基于突变的模糊测试不断地选择一些预先定义的突变算子来突变种子测试用例。不同的模糊测试有不同的方案来选择操作者。例如,AFL在三个阶段使用了三种不同的调度方案,如图1所示。
1.确定性阶段调度程序: AFL对第一次选择变异的种子测试用例应用确定性调度方案。该调度程序按顺序使用6种确定类型的突变操作符,并将它们逐个应用于种子测试用例。例如,它将应用位翻转8/8来翻转种子测试用例的每个字节。
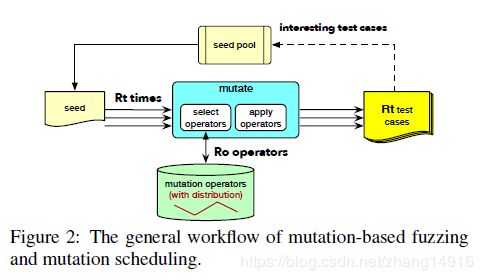
2.havoc阶段调度程序:在随机阶段采用了AFL的主要突变调度方案。如图2所示,AFL首先决定要在这个阶段生成的新测试用例的数量,用RT表示。每一次,AFL都会按照均匀分布的方式选择一系列的RO突变算子,并将它们应用到种子上,生成一个测试用例。在生成了RT新的测试用例之后,随机阶段就结束了。
3.拼接阶段调度程序:在一些罕见的情况下,AFL通过上述两个阶段为所有种子工作,但未能发现任何独特的崩溃或路径在一轮。然后AFL将进入一个特殊的拼接阶段。在这个阶段,AFL只使用一个操作符交叉来生成新的测试用例。这些新的测试用例将被发送到HAVOC阶段调度程序,而不是被测试的程序,以生成新的测试用例。
第一阶段的变异调度器具有确定性和缓慢性,而最后阶段的变异调度器很少使用。如图2所示,havoc阶段的调度程序更通用,已被许多模糊测试广泛采用。因此,本文主要研究了在havoc阶段使用的调度器的改进,从而可以在大多数基于突变的模糊测试中实现。更具体地说,我们的目标是找到一个最佳的概率分布,然后调度程序可以选择更好的变异算子,提高模糊效率。
2.4突变效率
不同的突变算子的工作方式完全不同。一个直观的假设是,它们在不同的目标程序上有不同的效率。有些在生成测试用例(称为有趣的测试用例)方面比其他更好,这些测试用例可以触发新的路径或崩溃。为了验证我们的假设,我们在AFL上进行了一个实验来评估每个操作者的效率。为了使评价结果具有确定性,我们只测量了确定性阶段12个变异算子产生的有趣的测试用例。结果如图3所示。
 图3:在AFL的确定阶段,不同操作员产生的有趣测试用例的百分比。
图3:在AFL的确定阶段,不同操作员产生的有趣测试用例的百分比。
在确定性阶段,突变算子的顺序和选择时间是固定的。图4显示了AFL在AVCONV模糊测试过程中选择操作人员的顺序和次数,表明了模糊测试所花的时间。
不同的变异算子对一个目标程序的效率是不同的。对于大多数程序,操作程序bitfilp 1/1、bitfilp 2/1和arith 8/8可以产生比其他操作程序更有趣的测试用例。另一方面,其他几个突变算子,如位翻转16/8、位翻转32/8和算术32/8,只能产生不到2%的有趣测试用例。
每个操作员的效率因目标程序而异。操作员可以在一个程序上产生良好的输出,但在另一个程序上失败。例如,ARITH 8/8在exiv2和tiff2bw上表现良好,但在avconv上只找到12%的有趣测试案例。
AFL将大部分时间花在确定性阶段。我们记录每个阶段花费的时间以及每个阶段在24小时内发现的有趣测试用例的数量,如图5所示。我们首先分析一个特殊的案例。对于tiff2bw,由于AFL找不到更有趣的测试用例,因此它完成了模糊队列中所有输入的确定阶段,并长时间跳过了确定阶段。然后,AFL将大部分时间花在havoc阶段,却一无所获。对于其他三种情况,AFL将70%以上的时间花在确定性阶段。模糊AVCONV时,AFL甚至不能在24小时内完成第一次输入的确定阶段。另一个重要的观察是,与确定性阶段相比,havoc阶段在发现有趣的测试用例方面更有效。此外,由于AFL在一个输入的确定阶段花费了太多时间,因此在给定的24小时内对avconv和pdfimages进行模糊处理时,它无法从模糊队列中的后期输入生成测试用例。注意,由于拼接阶段只使用交叉转换来改变测试用例,因此与将测试第2.3节中提到的目标程序的其他阶段相比,它花费的时间太少,无法在图5中显示。
AFL花大量时间在低效的突变操作上。图3表明,突变算子bitfilp1/1和bitfilp2/1发现了最有趣的测试用例。但根据图4,它们只被选择了少量的次数。另一方面,低效操作被频繁地选择,但很少产生感兴趣的测试用例,这降低了模糊测试效率。
动机: 基于以上分析,我们发现不同的突变算子具有不同的效率。因此,现有模糊测试中的突变调度程序遵循一些预先定义的分布,是不有效的。理想情况下,应该将更多的时间花在能够更好地生成有趣测试用例的突变操作上。因此,需要一个更好的突变调度器。
3.Overview of MOPT
3.1 Design Philosophy
突变调度器的目标是为给定的运行时上下文选择下一个最佳的突变操作符,它可以找到更有趣的测试用例。我们将这个问题简化为寻找一个最优的变异算子概率分布,然后调度程序在测试目标程序时选择下一个算子。
寻找所有变异算子的最优概率分布是一个挑战。相反,我们可以先让每个操作符探索自己的最佳概率。然后,基于这些最优概率,得到突变算子的全局最优概率分布。
粒子群优化(PSO)算法可以用来寻找算子的最优分布,并在我们的设置中详细描述了PSO的修改。
3.2 Particle Swarm Optimization (PSO)
Eberhart和Kennedy提出了PSO[20]算法,旨在寻找问题的最优解。它使用多个粒子迭代搜索解空间,其中位置是一个候选解。
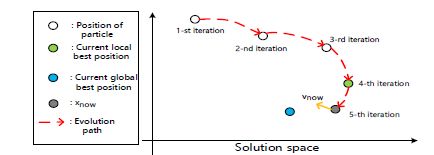
如图6所示,在每次迭代中,每个粒子移动到新的位置xnow是根据(1)其惯性(即先前的运动vnow),(2)位移到该粒子迄今为止发现的局部最佳位置lbest,以及(3)位移到所有粒子迄今为止发现的全局最佳位置gbest,将每个粒子移动到新的位置xnow。具体来说,粒子p的运动计算公式如下:
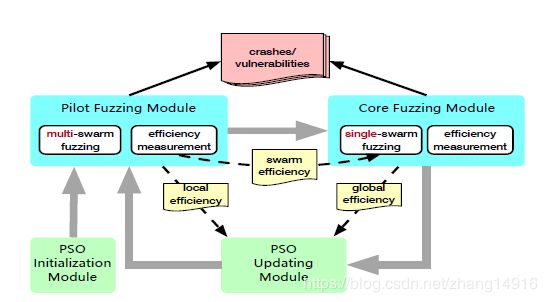
其中w是惯性权重,r满足0 因此,每个粒子都朝着LBEST和GBEST移动,并且很可能继续朝着更好的位置移动。通过向gbest移动,多个粒子可以同步工作,避免陷入局部最优状态。因此,群将得到最优解。另外,粒子群算法易于实现,计算成本低,适合于优化变异调度。 MOPT的目标是找到一个最佳的概率分布。我们提出了一种定制的粒子群算法,它不是直接用粒子来探索候选分布,而是先探索每个算子的最优概率,然后构造最优概率分布。 MOPT使用每个操作符作为一个粒子,并尝试在预定义的概率空间[xmin,xmax]中为每个操作符探索一个最佳位置,其中0 粒子(即操作符)在概率空间(即xnow)中的当前位置表示调度程序选择该操作符的概率。由于概率的性质,一次迭代中所有粒子的概率之和应规范化为1。 与粒子群优化算法类似,MOPT也指定了粒子所处的最佳位置作为其局部最佳位置。 对于一个给定的粒子,位置x1比x2更好,如果且仅当,其相应的操作符在前一位置比后者生成更有趣的测试用例(具有相同数量的调用)。因此,lbest是粒子的位置,在该位置对应的运算符生成更多有趣的测试用例(给定相同数量的调用)。 为了进行这种比较,对于每个粒子(即操作符),我们测量它的局部效率e f fnow,即,由该操作符贡献的有趣测试用例的数量除以在一次迭代中该操作符的调用数量。我们将最大的e f fnow表示为e f fbest。因此,lbest是操作员在历史上获得e f fbest的位置。 粒子群算法将所有粒子的最佳位置指定为全球最佳位置。请注意,与在统一解空间中移动粒子的原始粒子群算法不同,MOPT在不同的概率空间(形状和大小相同)移动粒子。因此,没有唯一适合所有粒子的全局最佳位置。相反,不同的粒子在这里有不同的全局最佳位置(在不同的空间中)。在粒子群算法中,全局最优位置取决于不同粒子之间的关系。因此,我们还通过一次评估多个粒子群,从全局的角度评估每个粒子的效率,称为globaleff 更具体地说,我们测量了迄今为止每个操作者在所有群中贡献的有趣的测试用例的数量,并将其用作粒子的globaleff。然后计算所有粒子的全局效率分布。对于每个操作符(即粒子),其全局最佳位置gbest定义为其globaleff在该分布中的比例。通过这种分布,效率更高的粒子(即操作员)可以获得更高的被选择的概率。 考虑到粒子、局部最佳位置和全局最佳位置的定义,我们可以采用PSO算法来逼近最优解(即突变算子的特定概率分布)。 然而,与已有的粒子群算法不同,MOPT定义的粒子群算法实际上只在解空间中探索一个候选解(即概率分布),因此可能陷入局部最优。因此,MOPT使用多个群,并将定制的PSO算法应用于每个群,如图7所示,以避免局部最优。 这些群之间需要同步。MOPT简单地以最有效的群体为最佳,利用其分布来调度模糊测试过程中的突变。在这里,我们将群的效率(称为swrameff)定义为该群贡献的有趣测试用例数除以一次迭代中的新测试用例数。 概述:总之,MOPT使用多个群,并将定制的PSO算法应用于每个群。在模糊测试过程中,在PSO的每次迭代中都会执行以下三个额外的任务 T1:定位每个群中所有粒子的局部最佳位置。在每个群中,每个粒子在一次迭代中的局部效率e f fnow在模糊测试过程中被评估。对于每一个粒子,历史上效率最高的e f fbest被标记为其局部最佳位置lbest。 T2:确定所有粒子在群中的最佳位置。每一个粒子的全局效率globaleff是通过群评估的。然后评估粒子的整体效率分布。在这个分布中,每个粒子的globaleff的比例被用作其全局最佳位置gbest。 T3:选择最好的群来引导模糊测试。在一次迭代中对每个群的效率swarmeff进行了评估。选择了swarmeff最大的群,并将其在当前迭代中的概率分布用于进一步的模糊化。 然后,在每次迭代结束时,mopt以与pso类似的方式移动每个群中的粒子。更具体地说,对于群体si中的粒子pj,我们更新其位置如下。 其中w是惯性权重,r满足0 此外,我们规范化这些位置以满足一些约束。首先,调整每个粒子的位置以适应概率空间[xmin;xmax]。然后,对于每个群,其所有粒子的位置(即概率)将被标准化,这样这些概率的总和等于1。 在更新了所有粒子群中所有粒子的位置后,模糊测试可以继续将这些粒子移动到新的位置,并进入一个新的粒子群算法迭代。 如图8所示,MOPT由四个核心模块组成,即PSO初始化和更新模块,以及pliot模糊测试和core模糊测试模块。 PSO初始化模块的运行用于设置PSO算法的初始参数。其他三个模块组成一个迭代循环,共同工作,不断模糊目标程序。 在循环的每次迭代中,粒子群算法粒子更新一次。为了用粒子群算法更新粒子的位置,需要在每次迭代中找出每个粒子的局部最佳位置和全局最佳位置。 利用该迭代回路,模糊器可以利用粒子群算法寻找最优的概率分布来选择变异算子,并逐步提高模糊效率。 注意,MOPT的工作流程独立于目标模糊测试,只要模糊测试的突变调度器使用概率分布来选择运算符。我们不需要改变目标模糊测试的行为,只需要评估模糊测试的效率,以移动粒子群优化算法粒子。对目标模糊测试的检测是最小的,性能开销也很小。 因此,MOPT是一种通用实用的突变调度方案,可以应用于各种模糊测试 此模块初始化PSO算法的参数。更具体地说,mopt(1)用随机值设置每个群中每个粒子的初始位置xnow,并将一个群中所有粒子的xnow和归一化为1;(2)将每个群中每个粒子的运动vnow位移设为0.1;(3)将每个群中每个粒子的初始局部效率e f fnow设置为0;(4)将每个粒子群中每个粒子的初始局部最佳位置lbest设置为0.5;(5)将每个粒子群中每个粒子的初始全局最佳位置gbest设置为0.5。注意,当模糊测试开始运行时,初始化模块只执行一次。 该模块利用多个群进行模糊测试,每个群探索不同的概率分布。此模块按顺序评估每个群,并在生成新测试用例的可配置数字(表示为PeriodPilot)后停止测试群。特定群的模糊测试处理过程如下。 对于每一个群,其概率分布用于调度变异算子的选择和模糊测试目标程序。在模糊测试过程中,该模块将测量三个测量值:(1)特定粒子(即操作)提供的感兴趣测试用例的数量;(2)特定粒子的调用数量;(3)该群通过检测目标程序发现的感兴趣测试用例的数量。 每个粒子的局部效率(在当前群中)是第一次测量除以第二次测量。因此,我们可以找到每个粒子的局部最佳位置。当前群的效率是第三个测量值除以测试用例计数PeriodPilot。因此,我们可以找到最有效的群 该模块采用模糊测试模块选择的最佳群,利用其概率分布进行模糊测试。它将在生成新测试用例的可配置数字(表示为periodcore)后停止。 一旦它停止,我们就可以测量每个粒子所贡献的有趣的测试用例的数量,不管它属于哪个粒子群,从PSO初始化开始到现在。然后,我们可以计算出粒子之间的分布,并确定每个粒子的全局最佳位置。 注意,如果我们在引导模块中只使用一个群,那么核心模块可以与引导模块合并。 利用pilot和core模糊测试模块提供的信息,该模块按照方程3和4更新每个群中的粒子。 在更新每个粒子之后,我们将进入下一个PSO更新迭代。因此,我们可以接近最优群(即操作的概率分布),利用它来指导core模糊测试模块,并有助于提高模糊测试效率。 虽然MOPT在突变模糊测试中的应用是通用的,但我们认识到MOPT在应用于AFL等特定模糊测试时,其性能可以进一步优化。 基于广泛的经验分析,我们认识到AFL及其后代在确定性阶段花费的时间要比在破坏和拼接阶段花费的时间多,后者可以发现更多独特的崩溃和路径。因此,MOPT为基于AFL的模糊测试提供了一种优化,即引领模糊测试模式,有选择地避免了耗时的确定阶段。 具体地说,当mopt完成一个种子测试用例的变异时,如果长时间没有发现任何新的唯一崩溃或路径,即用户设置的t,那么它将有选择地禁用以下测试用例的确定性阶段。引领模糊测试的方式具有以下优点。 更具体地说,MOPT为AFL提供了两种类型的引领模糊测试模式,基于确定性阶段是否会被重新启用:(1)MOPT-AFL-tmp,当新的有趣的测试案例数量超过预定的阈值时,它将重新启用确定性阶段;(2)MOPT-AFL-ever,它将永远不会重新启用确定性阶段。在随后的模糊测试过程中处于初始阶段。 在这一部分中,我们总结了现有的模糊机制和相关的种子选择策略。 基于突变的模糊测试。AFL是一种公认的模糊测试工具,因为它的高效率和易用性[17]。基于AFL[5,6]开发了多个有效模糊测试工具。为了提高模糊测试的性能,一些人将基于突变的模糊测试与其他缺陷检测技术结合起来[14、15、16、45]。另一种改进基于突变的模糊测试的方法是基于覆盖的模糊测试[7,11,12]。提出了一个名为qsym的快速混合执行引擎,以帮助模糊测试探索更多的错误和路径[42]。通过求解无符号执行的路径约束,Chen等人提出了angora。可以显著增加项目的分支覆盖率[10]。 本文提出的MOPT是一种改进测试用例突变过程,生成高质量突变测试用例的方案。利用其兼容性,它可以与上述大多数模糊测试工具组合使用。虽然本论文主要是利用MOPT来改进基于突变的模糊测试,但如果存在选择合适的操作人员来生成测试用例的问题,也可以在其他类型的模糊测试中实现,如generation-based fuzzers和kernel fuzzers。MOPT还可以与大多数现有的种子选择策略相结合,因为它们可以为模糊测试提供更好的初始种子集。我们将简要介绍这些领域的最新相关作品,如下所示。 Generation-based fuzzing——Generation-based fuzzing关注的是那些需要特定输入格式的测试用例的程序[46,47,48]。最近,Wang等人提出了一种新的数据驱动的种子生成方法skyfire来为XML和XSL生成有趣的测试用例[1]。Godefroid等人提出了一种基于RNN的机器学习技术,用于自动生成复杂输入格式的测试用例语法[49]。 其他模糊测试策略——几项研究提出了有效的kernel fuzzers[50,51]。许等。[13]实现了三种新的操作原语,有利于大规模模糊测试和基于云的模糊测试服务。你等。介绍了Semfuzz,以从漏洞相关文本中学习并自动生成概念验证(PoC)漏洞[52]。彼得斯等。建议slowfuzz触发算法复杂性漏洞[35]。克莱等人。进行了大量的实验,并提出了一些改进引信实验评估的准则[38]。一些作品提出了最先进的定向灰盒引信,以快速到达目标程序位置[21,53]。近年来,一些著作[8]、[9]将增强学习算法作为突变调度程序,分别提出了它们的模糊框架。然而,基于实验结果,这些方法的性能改进是有限的。 种子选择策略。一些研究集中在如何选择更好的种子集[2,3,4]。尼克尔斯等人。结果表明,使用生成的gan文件重新初始化afl可以找到ethkey的更独特路径[54]。LV等人。介绍了利用机器学习算法为不同输入格式生成高质量种子文件的SmartSeed[55]。根据实验结果,方法是有限的。 3.3设计细节
3.3.1Particles
3.3.2 Local Best Position Lbest
3.3.3 Global Best Position Gbest
3.3.4 Multiple Swarms
4 Implementation of MOPT
4.1 MOPT Main Framework
4.1.1 PSO Initialization Module
4.1.2 Pilot Fuzzing Module
4.1.3 Core Fuzzing Module
4.1.4 PSO Updating Module
4.2 Pacemaker Fuzzing Mode
8 Related Work