机器学习实战(十二)降维(PCA、SVD)
目录
0. 前言
1. 主成分分析PCA(Principal Component Analysis)
2. 奇异值分解SVD(Singular Value Decomposition)
3. 低维空间维度的选择
3.1. PCA
3.2. SVD
3.3. 平均投影误差的平方
4. 实战案例
4.1. PCA降维
4.2. SVD降维
4.3. SVD压缩存储矩阵
学习完机器学习实战的降维,简单的做个笔记。文中部分描述属于个人消化后的理解,仅供参考。
本篇综合了先前的文章,如有不理解,可参考:
吴恩达机器学习(十二)主成分分析
所有代码和数据可以访问 我的 github
如果这篇文章对你有一点小小的帮助,请给个关注喔~我会非常开心的~
0. 前言
数据的特征数量,又称作向量的维度。降维(dimensionality reduction)是通过一些方法,减少数据的特征数量,以降低维度。
- 数据压缩,减小占用的存储空间
- 加快算法的计算速度
- 低维平面可以可视化数据
主要有几种降维的方法:
- 主成分分析(PCA):将数据映射到低维度的新坐标轴上,以降低维度
- 因子分析(FA):假设数据由隐变量和噪声组成,通过找到隐变量,就可以降维
- 独立成分分析(ICA):假设数据是由多个数据源混合组成,通过找到数据源,就可以实现降维
本篇主要介绍PCA和利用SVD将数据映射到低维度上。
PCA:
- 优点:降低数据的复杂性,识别最重要的多个特征
- 缺点:不一定需要,且可能损失有用信息
- 适用数据类型:数值型数据
SVD:
- 优点:简化数据,去除噪声,提高算法的结果
- 缺点:数据的转换可能难以理解
- 适用数据类型:数值型数据
数据是指接受的原始材料,其中可能包含噪声和不相关信息,而信息是指数据中的相关部分。
降维技术通常能使得数据变得更容易使用,去除数据中的噪声,获取数据集中的信息量。
1. 主成分分析PCA(Principal Component Analysis)
PCA 基于最大方差理论,寻找低维度的坐标系,使得各个数据点到平面的投影距离最小,如下图所示(图源:机器学习实战):
若数据投影到坐标轴A上,则各个数据点的投影距离之和大,若数据投影到坐标轴B上,则各个数据点的投影距离之和小,所以应选择坐标轴B。最大方差理论表明,数据投影在坐标轴B上时,数据的方差最大,所以这条坐标轴最能表示原始数据。
若低维坐标系的维度为 ![]() ,则选定每一条坐标轴都需要与先前的所有坐标轴正交,且在剩下的空间中具有最大方差。
,则选定每一条坐标轴都需要与先前的所有坐标轴正交,且在剩下的空间中具有最大方差。
PCA 的算法流程:
- 将数据进行均值归一化
- 计算数据的协方差矩阵(协方差矩阵维度为
 )
) - 计算协方差矩阵的特征值和特征向量(特征值个数为
 ,特征向量维度为
,特征向量维度为  )
) - 将特征值从大到小排序,取前
 个特征值的特征向量
个特征值的特征向量 - 通过特征向量,将数据映射到新的空间中,维度为
 (原始数据维度为
(原始数据维度为  ,特征向量维度为
,特征向量维度为 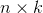 )
)
将低维数据映射到高维空间的估计点上,可将降维后的数据乘以特征向量的转置即可。
2. 奇异值分解SVD(Singular Value Decomposition)
SVD 同样可以去除数据中的噪声,用较小的数据集表示原始数据集,实现降维。
SVD 又可以称作隐性语义索引(Latent Semantic Indexing,LSI)或者隐性语义分析(Latent Semantic Analysis,LSA)。
通过 SVD 会构建出多个奇异值,这些奇异值代表数据的主成分,可以想象成是一个新的空间。
SVD 会进行矩阵分解,将原始矩阵分解为 ![]() :
:
![]()
其中,矩阵 ![]() 只包含对角线元素,其他元素为
只包含对角线元素,其他元素为 ![]() ,对角线元素从大到小排列,称为奇异值(Singular Value)。
,对角线元素从大到小排列,称为奇异值(Singular Value)。
奇异值与特征值有一定的联系,奇异值代表矩阵 ![]() 特征值的平方根。
特征值的平方根。
在选定前 ![]() 个奇异值后,可以通过矩阵
个奇异值后,可以通过矩阵 ![]() 将数据映射到新的空间,实现降维。
将数据映射到新的空间,实现降维。
SVD 的算法流程:
- 将数据进行均值归一化
- 计算数据的协方差矩阵(协方差矩阵维度为
 )
) - 对协方差矩阵进行奇异值分解(奇异值个数为
 ,矩阵
,矩阵 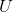 的维度为
的维度为  )
) - 将奇异值从大到小排序,取前
 个奇异值,取矩阵
个奇异值,取矩阵 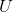 的前
的前  列
列 - 通过矩阵
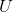 的前
的前  列,将数据映射到新的空间中,维度为
列,将数据映射到新的空间中,维度为  (原始数据维度为
(原始数据维度为  ,矩阵
,矩阵 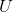 的前
的前  列维度为
列维度为 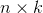 )
)
将低维数据映射到高维空间的估计点上,可将降维后的数据乘以矩阵 ![]() 的前
的前 ![]() 列的转置即可。
列的转置即可。
SVD 还可用少量主成分表示原始数据,例如选定前 ![]() 个奇异值,原始数据可近似表示如下:
个奇异值,原始数据可近似表示如下:
![]()
SVD 通过对数据降维,实现少量主成分表示原始数据,可以实现矩阵的压缩存储,在需要还原矩阵时,通过上式子还原即可。
3. 低维空间维度的选择
3.1. PCA
在 PCA 的计算中,通过查看特征值,可以选定低维度 ![]()
3.2. SVD
在 SVD 的计算中,通过查看奇异值,可以选定低维度 ![]()
3.3. 平均投影误差的平方
已知寻找一个低维平面,需要使得各个数据点到这个平面的距离最小,这个距离可采用平均投影误差的平方量化,定义如下
其中,![]() 是低维空间点映射会高维空间中的估计点。
是低维空间点映射会高维空间中的估计点。
自定阈值 ![]() 用来选定低维度
用来选定低维度 ![]() :
:
4. 实战案例
以下将展示书中案例的代码段,所有代码和数据可以在github中下载:
4.1. PCA降维
# coding:utf-8
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
"""
pca降维
"""
# 加载数据集
def loadDataSet(fileName, delim):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()]
datArr = [list(map(float, line)) for line in stringArr]
return mat(datArr)
# 加载包含NaN的数据集
# 用平均值代替缺失值
def replaceNanWithMean(fileName, delim):
datMat = loadDataSet(fileName, delim)
numFeat = shape(datMat)[1]
for i in range(numFeat):
meanVal = mean(datMat[nonzero(~isnan(datMat[:, i].A))[0], i])
datMat[nonzero(isnan(datMat[:, i].A))[0], i] = meanVal
return datMat
# PCA算法
def pca(dataMat, topNfeat=9999999):
# 均值归一化
meanVals = dataMat.mean(axis=0)
maxVals = dataMat.max(axis=0)
minVals = dataMat.min(axis=0)
meanRemoved = (dataMat - meanVals) / (maxVals - minVals)
# 协方差矩阵
covMat = cov(meanRemoved, rowvar=0)
# 特征值,特征向量
eigVals, eigVects = linalg.eig(mat(covMat))
# 按照特征值从小到大排序,返回排序后索引
eigValInd = argsort(eigVals)
# 逆序取topNfeat个最大的特征的索引
eigValInd = eigValInd[:-(topNfeat + 1):-1]
# 获取特征向量
redEigVects = eigVects[:, eigValInd]
# 矩阵相乘,降低维度
lowDDataMat = meanRemoved * redEigVects
# 将原始数据重新映射会高维,用于调试
reconMat = multiply((lowDDataMat * redEigVects.T), (maxVals - minVals)) + meanVals
return lowDDataMat, reconMat
if __name__ == '__main__':
dataMat = loadDataSet('testSet.txt', '\t')
lowDMat, reconMat = pca(dataMat, 1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:, 0].flatten().A[0], dataMat[:, 1].flatten().A[0],
marker='^', s=90)
ax.scatter(reconMat[:, 0].flatten().A[0], reconMat[:, 1].flatten().A[0],
marker='o', s=50, c='red')
plt.show()
dataMat = replaceNanWithMean('secom.data', ' ')
meanRemoved = dataMat - dataMat.mean(axis=0)
covMat = cov(meanRemoved, rowvar=0)
eigVals, eigVects = linalg.eig(mat(covMat))
eigValInd = argsort(eigVals)
eigValInd = eigValInd[::-1]
sortedEigVals = eigVals[eigValInd]
total = sum(sortedEigVals)
varPercentage = sortedEigVals / total * 100
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1, 21), varPercentage[:20], marker='^')
plt.xlabel('Principal Component Number')
plt.ylabel('Percentage of Variance')
plt.show()
4.2. SVD降维
# coding:utf-8
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
"""
svd降维
"""
# 加载数据集
def loadDataSet(fileName, delim):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()]
datArr = [list(map(float, line)) for line in stringArr]
return mat(datArr)
# SVD降维
def svd(dataMat, topNfeat=9999999):
# 均值归一化
meanVals = dataMat.mean(axis=0)
maxVals = dataMat.max(axis=0)
minVals = dataMat.min(axis=0)
meanRemoved = (dataMat - meanVals) / (maxVals - minVals)
# 协方差矩阵
covMat = cov(meanRemoved, rowvar=0)
# 奇异值分解
U, sigma, VT = linalg.svd(covMat)
# 降维
lowDDataMat = meanRemoved * U[:, :topNfeat]
# 映射回高维空间中,不过不是原始值,而是低维空间点对应的高维空间位置
reconMat = multiply((lowDDataMat * U[:, :topNfeat].T), (maxVals - minVals)) + meanVals
return lowDDataMat, reconMat
if __name__ == '__main__':
dataMat = loadDataSet('testSet.txt', '\t')
lowDMat, reconMat = svd(dataMat, 1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:, 0].flatten().A[0], dataMat[:, 1].flatten().A[0],
marker='^', s=90)
ax.scatter(reconMat[:, 0].flatten().A[0], reconMat[:, 1].flatten().A[0],
marker='o', s=50, c='red')
plt.show()
4.3. SVD压缩存储矩阵
# coding:utf-8
from numpy import *
from numpy import linalg as la
"""
svd降维实现矩阵压缩
"""
# 输出矩阵
def printMat(inMat, thresh=0.8):
for i in range(32):
s = ''
for k in range(32):
if float(inMat[i, k]) > thresh:
s += '1'
else:
s += '0'
print(s)
# 降维压缩矩阵
def imgCompress(numSV=2, thresh=0.8):
myl = []
for line in open('0_5.txt').readlines():
newRow = []
for i in range(32):
newRow.append(int(line[i]))
myl.append(newRow)
myMat = mat(myl)
# 打印原始矩阵
print("****original matrix******")
printMat(myMat, thresh)
# svd压缩矩阵
# U: m*m
# sigma: m*n
# VT: n*n
U, Sigma, VT = la.svd(myMat)
# 构建sigma矩阵
SigRecon = mat(zeros((numSV, numSV)))
for k in range(numSV):
SigRecon[k, k] = Sigma[k]
# 利用压缩后的矩阵还原原矩阵
reconMat = U[:, :numSV] * SigRecon * VT[:numSV, :]
# 打印还原后的矩阵
print("****reconstructed matrix using %d singular values******" % numSV)
printMat(reconMat, thresh)
if __name__ == '__main__':
imgCompress(2)
如果这篇文章对你有一点小小的帮助,请给个关注喔~我会非常开心的~


