【深度学习】Mixup: Beyond Empirical Risk Minimization
博主整理了近几年混合样本数据增强(Mixed Sample Data Augmentation)相关论文和代码,并分享在github上,地址如下,
https://github.com/JasonZhang156/awesome-mixed-sample-data-augmentation
如果大家对混合样本数据增强算法有兴趣,可以star或者fork到自己的仓库。
博主会对内容持续更新!
一、相关理论
Mixup是MIT和FAIR在ICLR 2018上发表的文章中提到的一种数据增强算法。在介绍mixup之前,我们首先简单了解两个概念:经验风险最小化(Empirical risk minimization,ERM)和邻域风险最小化(Vicinal Risk Minimization,VRM)。
“经验风险最小化”是目前大多数网络优化都遵循的一个原则,即使用已知的经验数据(训练样本)训练得到的学习器的误差或风险,也叫作“经验误差”或“训练误差”。相对的,在新样本(未知样本)上的误差称为“泛化误差”,显然,我们希望学习器的“泛化误差”越小越好。然而,通常我们事先并不知道新样本是什么样的,实际能做的是努力使经验误差越小越好。但是,过分的减小经验误差,通常会在未知样本上产生很差的结果,也就是我们常说的“过拟合”。
关于“泛化性”,通常可以通过使用大规模训练数据来提高,但是实际上,获取有标签的大规模数据需要耗费巨大的人工成本,甚至有些情况下根本无法获取数据。解决这个问题的一个有效途径是“邻域风险最小化”,即通过先验知识构造训练样本的邻域值。一般的做法就是传统的数据增强方法,比如加噪、翻转、缩放等,但是这种做法很依赖于特定的数据集和人类的先验知识。
二、算法介绍
Mixup是一种一般性(不针对特定数据集)的邻域分布方式,可以表示为,
其中,λ ~Beta(α, α),α ∈ (0, ∞)。从上式可以看出,mixup以线性插值的方式来构建新的训练样本,
其中,(xi , yi ) 和 (xj , yj )是从原始训练数据中随机选取的两个样本,λ ∈ [0, 1]。α是mixup的超参数,控制两个样本插值的强度,当α → 0时,则退化到了ERM的情况。
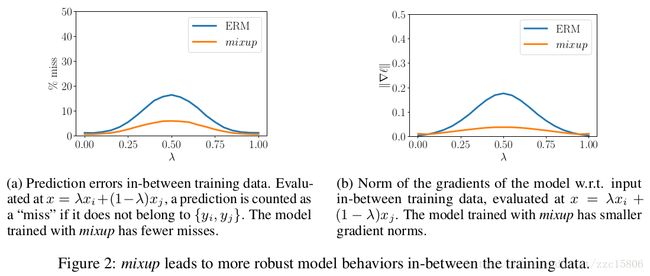
上图展示了mixup和ERM的性能对比图,可以看出mixup方法能够产生更鲁棒的结果。
三、算法实现
下面给出mixup的python版本,
def get_batch(x, y, step, batch_size, alpha=0.2):
"""
get batch data
:param x: training data
:param y: one-hot label
:param step: step
:param batch_size: batch size
:param alpha: hyper-parameter α, default as 0.2
:return:
"""
candidates_data, candidates_label = x, y
offset = (step * batch_size) % (candidates_data.shape[0] - batch_size)
# get batch data
train_features_batch = candidates_data[offset:(offset + batch_size)]
train_labels_batch = candidates_label[offset:(offset + batch_size)]
# ERM
if alpha == 0:
return train_features_batch, train_labels_batch
# mixup
if alpha > 0:
weight = np.random.beta(alpha, alpha, batch_size)
x_weight = weight.reshape(batch_size, 1, 1, 1)
y_weight = weight.reshape(batch_size, 1)
index = np.random.permutation(batch_size)
x1, x2 = train_features_batch, train_features_batch[index]
x = x1 * x_weight + x2 * (1 - x_weight)
y1, y2 = train_labels_batch, train_labels_batch[index]
y = y1 * y_weight + y2 * (1 - y_weight)
return x, y四、总结
Mixup的实现方法非常简单,只需几行代码,却取得了非常惊人的效果。论文中的实验包括我自己在做一些分类任务时,使用mixup的性能都要优与常规的方法,是一项很有意义的工作。
【参考文献】
[1] mixup: Beyond Empirical Risk Minimization
[2] https://en.wikipedia.org/wiki/Empirical_risk_minimization