【Coursera】Machine learning - week6 : Advice for Applying Machine Learning

之前的几个周一直没有写，这个周才突然意识到应该写一下博客，因此现在才开始，后面再补好了。

这个文章的目的，主要在于梳理一下视频中的知识点。

1、train set、validation set、test set

Training set: A set of examples used for learning, which is to fit the parameters [i.e., weights] of the classifier.
Validation set: A set of examples used to tune the parameters [i.e., architecture, not weights] of a classifier, for example to choose the number of hidden units in a neural network.
Test set: A set of examples used only to assess the performance [generalization] of a fully specified classifier.

上述Ripley, B.D是对训练集、验证集和测试集的解释。而我个人对它们的理解，则是如下：

train set：如名字所说，它是用于训练的集合，是希望通过数据得到该模型在对应数据下的最佳参数，简而言之，train set决定了参数的选择。比如对于一个线性回归来说，它决定了theta的取值。

validation set：该集合的作用是对模型结构的选择。如视频中提到的线性回归。我们首先用对不同幂次d的模型在train set上进行拟合，然后再在validation set上测试其效果。那么简化来看，其实是在以validation set作为训练数据，以模型的幂次d为参数，在validation集上面取到一个最优的值。因此说validation set的主要作用是对模型进行选择。

test set：前面两个集的作用，分别是模型的训练和选择，那么我们还需要一个集合，来测试我们当前已经选择好的模型的表现如何。那么test集的作用就是评测所得模型的效果。而不直接用validation error来作为模型的评测结果的原因，是因为我们是在validation set上取的最优值，因此其在validation set上的效果肯定是较好的，所以才需要用test set来进行测试。

2、bias and variance

bias，即某个模型的期望输出与目标输出的相同程度的度量，其中bias越高，代表期望与目标相差越远。

variance，即某个模型在面对不同的数据时，它的期望输出发生变动的程度。（这里与我们平时见到的方差是同一概念）

如上图，high bias与underfitting是相对应的，此时的train error与validation error同时处于一个较高的水平。

high variance与overfitting是相对应的，此时的train error较小，而validation error较大。

3、regularization parameter --lambda

lambda在规则化的线性回归中的作用是对较大的参数进行一些惩罚，若取的值合适则可以防止overfitting，反之若取的值过大则有可能会导致underfitting。将bias和variance以函数值，lambda为参数的话，则会得到如下所示图

其中lambda过小则会导致variance过大，lambda过大则会导致bias过小，因此要多次测试选择合适的lambda。

4、learning curves

learning curves是由train set size m为横坐标，train error 和validation error为纵坐标所作曲线。通过该曲线我们可以判断，当前模型是处在high bias、high variance or just right。

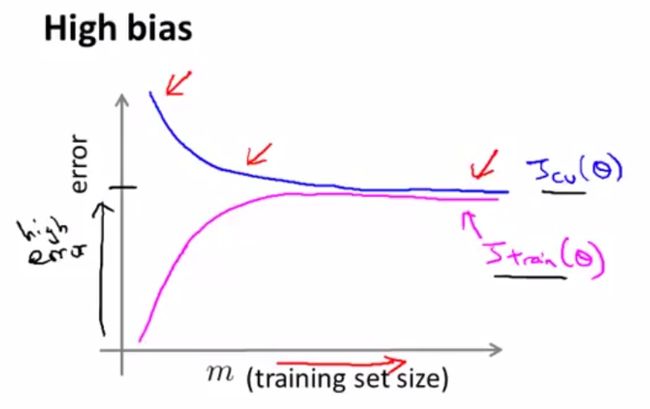
high bias，此时偏差较高，train error和validation error都比较高，并且再多的数据也不能使得模型进一步优化。

此时train error和validation error还有着比较大的差异，可以看到的是，如果增加数据量可以使得模型得到进一步的优化。

而下图是just right的曲线图。

通过上面几张图我们可以分析得到：

1）特征的个数是受着能够得到的数据量的大小的制约的。

2）只要数据足够多，便可以消除过拟合。

5、precision & recall

首先需要先介绍一张图

其中从左到右从上到下依次是

True positive（TP，真阳，样本真值为1&预测为1）

False positive（FP，假阳，样本真值为0&预测为1）

False negative（FN，假阴、样本真值为1&预测为0）

True negative（TN，真阴，样本真值为0&预测为0）

那么现在就可以定义precision & recall

precision，也称作查准率，量化对正样本预测的准确度，precision = TP / （TP + FP）

recall，也称作查全率，量化对正样本预测的完整度，recall = TP / （TP + FN）

可以知道，若是我们总是预测一个样本为1，那么recall率则将到达100%，但是precision则会低的惨不忍睹

若我们只在已经非常确定的时候再做出预测样本为1的判断，那么precision则会很高，但是recall率也会不忍直视

那么如何通过recall和precision评价模型的好坏成了一个问题

因此F1score检验横空出世

F = 2 × precision × recall / （precision + recall）

其中F值越大，代表该模型越可能更加优秀

（以上图片全是来自视频）