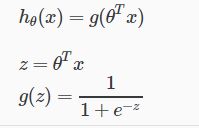吴恩达《Machine Learning》-Logistic Regression逻辑回归(六)
分类问题
为什么不用线性回归做分类问题(不使用)

使用线性回归,将所有大于0.5的预测映射为1,将所有小于0.5的预测映射为0。
先使用线性回归匹配数据,之后需要找到门限值,假设例子中门限值为hθ(x)=0.5。
把正负例子都投影到x轴。其中大于0.5的都为正例,小于0.5的都为负例。
![]()
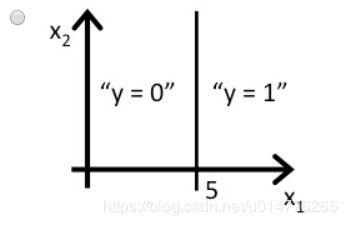
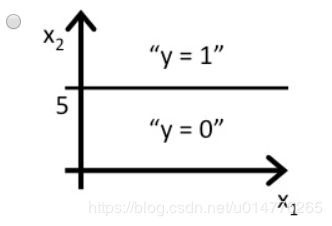
当有极端数据时,使用线性回归匹配数据。会导致回归线更偏向极端值,此时采用原本0.5的门限值,可能会导致分错。
使用线性回归做分类时,预测值可能会大于1或小于0。正常来说,逻辑回归做分类,预测值一定在[0,1]区间。
练习题:
![]()
选择(D)。
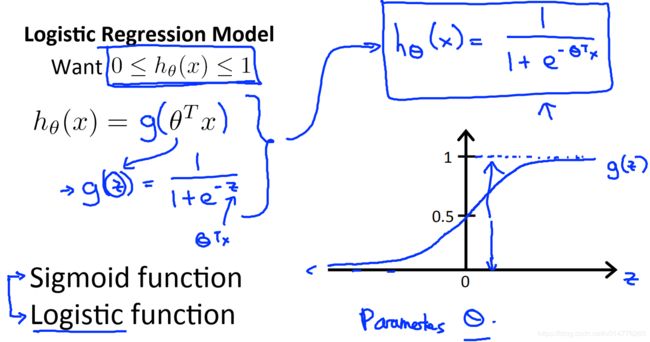
逻辑回归logistic regression
将传统线性回归hθ(x)=θ^Tx
基础上增加sigmod函数,成为hθ(x)=g(θ^Tx )=1/1+e-(θ^T*x),使用sigmod函数将线性回归的预测值,映射到0,1区间。

hθ(x) 给我们关于输出为正例的概率
条件概率,告诉病人有70%的概率肿瘤是恶性的。
练习题:

选择(A)。总概率为1,正例概率0.7.负例概率1-0.7=0.3
Decision boundary决策边界
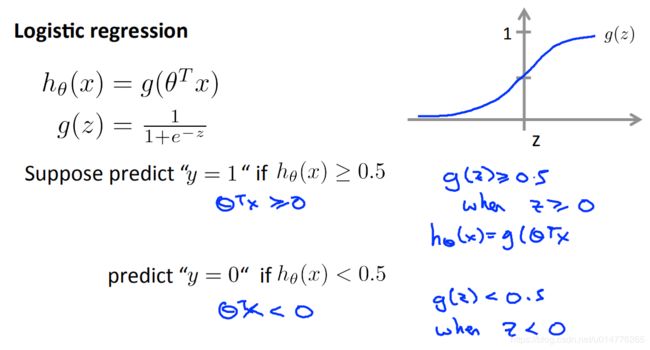
决定hθ(x)取值范围为多少时,预测值取正例或负例。
也就是Z大于等于0时,即g(Z)大于等于0.5时,取正例。
Z小于0时,即g(Z)小于0.5时,取负例。
sigmod函数总结
逻辑回归的sigmod函数公式

图像

极限
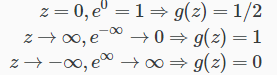


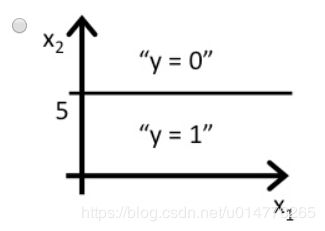
决策边界上方(hθ(x)>0.5)取正例,下方(hθ(x)<0.5)取负例。
示例:求决策边界
练习题:

可以使用多项式回归polynomial regression,即特征的高阶次方组合,来拟合更复杂的数据集。
训练集中的数据用来拟合θ参数,而不是决策边界。有了θ参数即可拟合出决策边界。
损失函数Cost Function

拥有m个样本,下标从x0-xn(n+1维向量)其中,x0=1.
y预测值应属于{0,1}
模型函数为hθ(x)

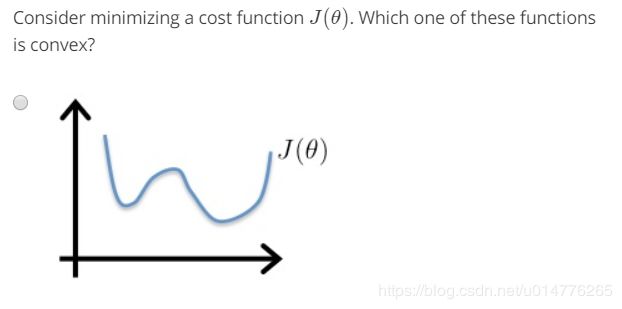
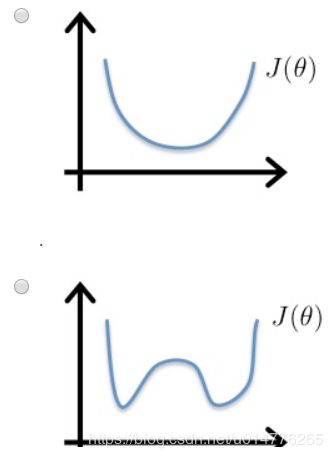
如果同线性回归的损失函数一样,将hθ(x)替换成sigmod函数,会产生一个非凸形函数(non-convex),使用梯度下降的话,可能找不到全局最优值。(只有凸函数convex可以使用梯度下降找到全局最优值)。
原因是:线性回归的hθ(x)为线性函数,而逻辑回归的hθ(x)为非线性函数。非线性函数 加上平方误差 必定产生非凸函数。
练习题:
逻辑回归的损失函数
向量化表达:
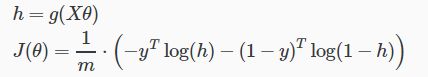
当y=1时的图像

y=1预测值为正例时的损失函数
当hθ(x)为1时,预测值y为1,此时损失函数为0
但是当hθ(x)趋近于0时,此时损失函数趋近于无穷。
也就是预测当预测值为1(正例时也就是肿瘤良性时)的概率为0,此时的损失函数非常大。此时几乎没有概率预测到肿瘤为恶性。
 y=0预测值为正例时的损失函数
y=0预测值为正例时的损失函数
当hθ(x)为0时,预测值y为0,此时损失函数为0
但是当hθ(x)趋近于1时,此时损失函数趋近于无穷。
也就是预测当预测值为0(反例时也就是肿瘤恶性时)的概率为0,此时的损失函数非常大。此时几乎没有概率预测到肿瘤为良性。
练习题:
![]()
选择(A,B,D)此题建议多看
A.只有损失函数最小,也就是损失函数为0时,才可以区分预测值为正例反例
D.如图所示
Simplified Cost Function损失函数简写
损失函数是使用概率论中的最大似然估计法 统计得来
![]()
逻辑回归的梯度下降
求偏导数,然后将J(θ)套入公式

将hθ(x)替换成新的sigmod函数即可
梯度下降公式
练习题:
向量法表示J(θ):
向量法表示偏导数:
其他优化算法
Conjugate gradient共轭梯度
BFGS L-BFGS
当数据量大的时候,建议使用上述优化算法。其速度更快。
优点:
不需要手动挑选学习率α,算法可以自动根据每轮的迭代,挑选每轮最佳的学习率α
速度比梯度下降更快
缺点:
更复杂

octave中调用无约束非线性规划下降算法
首先调用损失函数costFunction计算J(θ)与梯度。
之后传入fminunc中,选择合适的θ向量值。(注意:θ向量的维度 必须大于等于2)
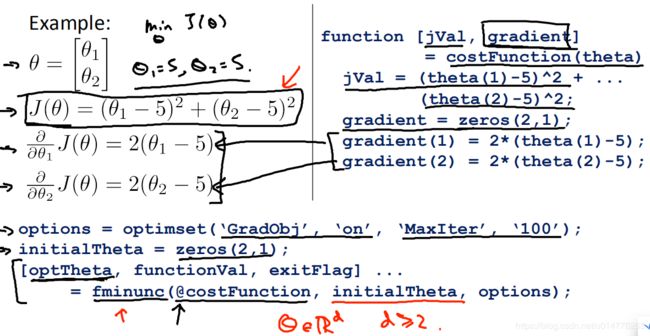
我们需要做的是编写一个损失函数。
练习题:


选择(C),gradient(1)是计算θ0的偏导数,gradient(2)是计算θ1的偏导数
Multiclass Classification多分类问题
解决方案:One-vs-all一对多问题
h(1)(x)将第一类作为正例,剩余其他类都看作负例。
h(2)(x),h(3)(x)以此类推。
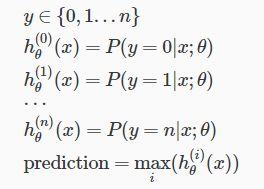
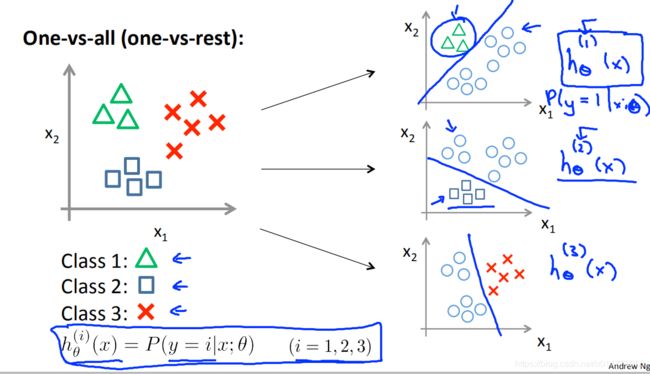
各个分类器的含义:
hθ(i)(x)就是当y=i预测值取第i类时的概率
对于一个新的样本,来预测其属于哪一个类别。只需要放入不同的分类器中,并选择当中概率最大的那个分类器。其对应的类别,即为新的样本所属的类别。

练习题:
测试题:

选择(A,B),正例的概率0.7.,故负例概率为0.3
![]()

选择(A,B)

选择(A,C)。hθ(x(i)-y(i))xj^(i)展开
hθ(x(1)-y(1))x0^(1) 故每次求和1-m,xj^(i)为一个数字。
换成向量写法后,为C选项。

选择(A,B)
A.m为样本种类数,逻辑回归分类 样本种类数一定大于等于1
D.高级优化函数只能加快收敛速度。优化函数只能停留在局部最优值,而不是全局最优值。是由于损失函数 不是凸函数。与优化函数无关。


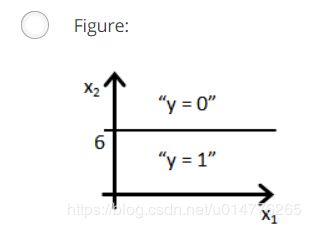

选择(B)。-6+x1>0,则x1>6时为正例。