数学建模 of python (一元线性回归问题)

来源：https://www.johnwittenauer.net/machine-learning-exercises-in-python-part-1/

今年，当我发现Coursera时，我职业发展的关键时刻之一就出现了。我听说过“MOOC”现象，但没有时间潜入课堂。今年早些时候，我终于取消了触发器并注册了Andrew Ng的机器学习课程。我从头到尾完成了整个过程，包括所有的编程练习。这种体验让我看到了这种教育平台的力量，从此我就被迷住了。

这篇博文将是安德鲁班级编程练习系列中的第一篇。我没有特别关心的课程的一个方面是使用Octave进行作业。尽管Octave / Matlab是一个很好的平台，但大多数真实世界的“数据科学”都是用R或Python完成的（当然还有其他语言和工具在使用，但这两个无疑是最重要的）。因为我正在尝试开发我的Python技能，所以我决定开始在Python中从头开始练习练习。完整的源代码可以在我在Github上的IPython repo中找到。如果您有兴趣，您还可以在根目录下找到这些练习中使用的数据和原始练习PDF文件。

虽然我可以在此过程中解释本练习中涉及的一些概念，但我无法传达您可能需要完全理解的所有信息。如果你真的对机器学习很感兴趣但还没有接触到它，我鼓励你查看课程（这是完全免费的，没有任何承诺）。有了它，让我们开始吧！

检查数据

在练习1的第一部分中，我们的任务是实施简单的线性回归来预测食品卡车的利润。假设您是一家餐厅特许经营店的首席执行官，并正考虑在不同的城市开设新店。该连锁店已在各个城市拥有卡车，您可以获得来自城市的利润和人口数据。您想知道新食品卡车的预期利润可能只给予该城市的人口。

让我们首先检查上面我的存储库的“data”目录中名为“ex1data1.txt”的文件中的数据。首先，我们需要导入一些库。

import os  
import numpy as np  
import pandas as pd  
import matplotlib.pyplot as plt  
%matplotlib inline

现在让我们开始吧。我们可以使用pandas将数据加载到数据框中，并使用“head”函数显示前几行。

path = os.getcwd() + '\data\ex1data1.txt'  
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])  
data.head()

	Population	Profit
0	6.1101	17.5920
1	5.5277	9.1302
2	8.5186	13.6620
3	7.0032	11.8540
4	5.8598	6.8233

pandas提供开箱即用的另一个有用功能是“describe”功能，它可以计算数据集的一些基本统计数据。这有助于在项目的探索性分析阶段获得数据的“感觉”。

data.describe()  

Population	Profit
count	97.000000	97.000000
mean	8.159800	5.839135
std	3.869884	5.510262
min	5.026900	-2.680700
25%	5.707700	1.986900
50%	6.589400	4.562300
75%	8.578100	7.046700
max	22.203000	24.147000

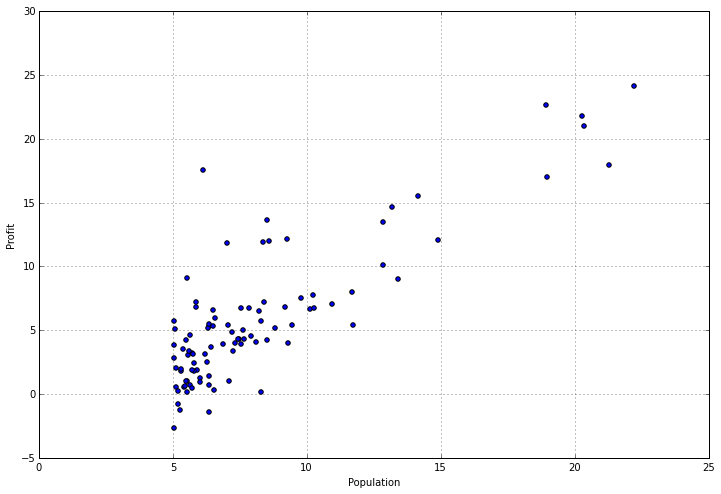
检查有关数据的统计数据可能会有所帮助，但有时您需要找到可视化数据的方法。幸运的是，这个数据集只有一个因变量，所以我们可以将它放在一个散点图中，以便更好地了解它的外观。我们可以使用pandas为此提供的“plot”功能，这实际上只是matplotlib的包装器。

data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8)) 

真正有助于实际查看正在发生的事情，不是吗？我们可以清楚地看到，人口较少的城市周围有一组价值观，随着城市规模的增加，利润增加呈线性趋势。现在让我们来看看有趣的部分 - 从头开始​​在python中实现线性回归算法！

实现简单线性回归

如果你不熟悉线性回归，它是一种建模因变量和一个或多个自变量之间关系的方法（如果有一个自变量那么它被称为简单线性回归，如果有多个自变量那么它就是称为多元线性回归）。线性回归有很多不同的类型和方差超出了本讨论的范围，所以我不会在这里讨论，但简单地说 - 我们试图创建一个数据X的线性模型，使用一些参数theta，用于描述数据的方差，以便给定一个不在X中的新数据点，Ÿ将没有真正知道什么ÿ是。

在此实现中，我们将使用称为梯度下降的优化技术来查找参数theta。如果您熟悉线性代数，您可能会意识到还有另一种方法可以找到称为“正规方程”的线性模型的最佳参数，它基本上使用一系列矩阵计算来解决问题。但是，这种方法的问题在于它不能很好地扩展到大型数据集。相比之下，我们可以使用梯度下降和其他优化方法的变体来扩展到无限大小的数据集，因此对于机器学习问题，这种方法更实用。

好的，这就足够了。我们来写一些代码。我们首先需要的是成本函数。成本函数通过计算模型对数据点的预测，使用模型参数和实际数据点之间的误差来评估模型的质量。例如，如果给定城市的人口是4并且我们预测它是7，则我们的误差是（7-4）^ 2 = 3 ^ 2 = 9（假设L2或“最小二乘”损失函数）。我们对X中的每个数据点执行此操作，并对结果求和以获得成本。这是功能：

def computeCost(X, y, theta):  
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

请注意，没有循环。我们利用numpy的线性algrebra功能将结果计算为一系列矩阵运算。这比未经优化的“for”循环计算效率更高。

为了使这个成本函数与我们上面创建的pandas数据框无缝地工作，我们需要做一些操作。首先，我们需要在数据框的开头插入一列1s，以使矩阵运算正常工作（我不会详细说明为什么需要这样做，但如果你是在练习文本中，那么它就在感兴趣 - 基本上它解释了线性方程中的截距项。其次，我们需要将数据分成独立变量X和我们的因变量y。

# append a ones column to the front of the data set
data.insert(0, 'Ones', 1)

# set X (training data) and y (target variable)
cols = data.shape[1]  
X = data.iloc[:,0:cols-1]  
y = data.iloc[:,cols-1:cols]  

最后，我们将把数据帧转换为numpy矩阵并实例化参数matirx。

# convert from data frames to numpy matrices
X = np.matrix(X.values)  
y = np.matrix(y.values)  
theta = np.matrix(np.array([0,0]))  

调试矩阵运算时要记住的一个有用技巧是查看正在处理的矩阵的形状。记住，当你走过头脑中的台阶时，矩阵乘法看起来像（ixj）*（jxk）=（ixk），其中i，j和k是矩阵相对尺寸的形状，这也很有帮助。

X.shape, theta.shape, y.shape  

（（97L，2L），（1L，2L），（97L，1L））

好的，现在我们可以尝试我们的成本函数。请记住，参数已初始化为0，因此解决方案尚未达到最优，但我们可以看到它是否有效。

computeCost(X, y, theta)  

32.072733877455676

到现在为止还挺好。现在我们需要使用练习文本中定义的更新规则定义一个函数来对参数theta执行梯度下降。这是梯度下降的功能：

def gradientDescent(X, y, theta, alpha, iters):  
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X * theta.T) - y

        for j in range(parameters):
            term = np.multiply(error, X[:,j])
            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))

        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost

梯度下降的想法是，对于每次迭代，我们计算误差项的梯度，以便找出移动我们的参数向量的适当方向。换句话说，我们正在计算对参数进行的更改以减少误差，从而使我们的解决方案更接近最优解（即最佳拟合）。

这是一个相当复杂的主题，我可以轻松地将整篇博文专门用于讨论梯度下降。如果您有兴趣了解更多信息，我建议您从本文开始并从那里开始分支。

我们再一次依靠numpy和线性代数来解决问题。您可能会注意到我的实现并非100％最优。特别是，有一种方法可以摆脱内部循环并立即更新所有参数。我将把它留给读者来解决它（我将在后面的文章中介绍它）。

现在我们已经有了评估解决方案的方法，以及找到一个好解决方案的方法，现在是时候将它应用到我们的数据集中了。

# initialize variables for learning rate and iterations
alpha = 0.01  
iters = 1000

# perform gradient descent to "fit" the model parameters
g, cost = gradientDescent(X, y, theta, alpha, iters)  
g  

矩阵（[[ - 3.24140214,1.1272942]]）

请注意，我们在这里初始化了一些新变量。如果仔细观察梯度下降函数，它会有一个名为alpha和iters的参数。Alpha是学习速率 - 它是参数更新规则中的一个因素，有助于确定算法收敛到最优解的速度。Iters只是迭代次数。如何初始化这些参数没有硬性规定，通常会涉及一些反复试验。

我们现在有一个参数向量描述我们认为是我们数据集的最佳线性模型。评估回归模型有多好的一种快速方法可能是查看数据集上新解决方案的总误差：

computeCost(X, y, g)  

4.5159555030789118

这肯定比32好很多，但它不是一个非常直观的方式来看待它。幸运的是，我们可以使用其他一些技术。

查看结果

我们现在将使用matplotlib来可视化我们的解决方案。还记得以前的散点图吗？让我们在数据的散点图上叠加一条代表我们模型的线，看它是否合适。我们可以使用numpy的“linspace”函数在我们的数据范围内创建一个均匀间隔的一系列点，然后使用我们的模型“评估”这些点，以查看预期的利润是多少。然后我们可以将它变成折线图并绘制它。

x = np.linspace(data.Population.min(), data.Population.max(), 100)  
f = g[0, 0] + (g[0, 1] * x)

fig, ax = plt.subplots(figsize=(12,8))  
ax.plot(x, f, 'r', label='Prediction')  
ax.scatter(data.Population, data.Profit, label='Traning Data')  
ax.legend(loc=2)  
ax.set_xlabel('Population')  
ax.set_ylabel('Profit')  
ax.set_title('Predicted Profit vs. Population Size') 

 

不错！我们的解决方案看起来像是数据集的最佳线性模型。由于梯度体面函数也在每次训练迭代时输出一个具有成本的向量，我们也可以绘制它。

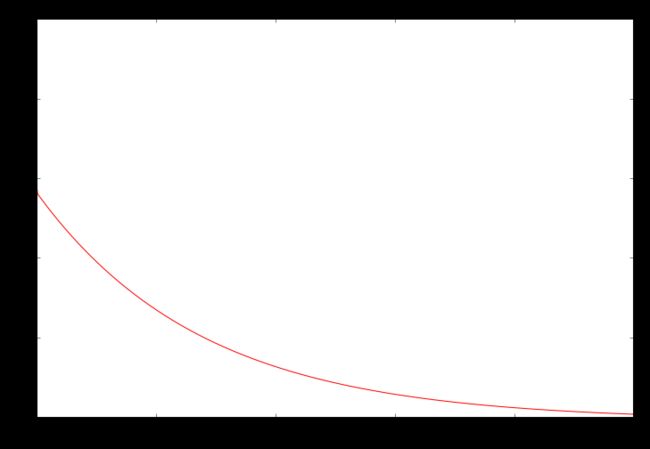
fig, ax = plt.subplots(figsize=(12,8))  
ax.plot(np.arange(iters), cost, 'r')  
ax.set_xlabel('Iterations')  
ax.set_ylabel('Cost')  
ax.set_title('Error vs. Training Epoch') 

请注意，成本总是降低 - 这是所谓的凸优化问题的一个例子。如果您要绘制问题的整个解空间（即将成本绘制为参数的每个可能值的模型参数的函数），您会看到它看起来像“碗”形状，其中“盆”代表最佳解决方案。

目前为止就这样了！在第2部分中，我们将通过将此示例扩展为多于1个变量来完成第一个练习。我还将展示如何通过使用名为scikit-learn的流行机器学习库来达到上述解决方案。