视觉SLAM——位姿估计

******看完位姿估计原理过一段时间又忘记了，现参考高翔视觉SLAM十四讲做本文笔记。
SLAM中的里程计都是基于特征点方式的算法。

1.特征匹配
特征匹配是视觉SLAM中极为关键的一步,它解决了数据关联问题。通过图像与图像或图像与地图间描述子进行准确匹配，可以为后续姿态估计、优化等操作减轻大量负担。由于图像特征的局部特性、误匹配、重复纹理等，仅利用局部特征很难解决问题。首先讨论图像与图像匹配情况。不同相机匹配原理不一样,2D-2D:对极几何, 3D-3D:ICP, 3D-2D: PnP,本文重点考虑3D-3D的情况。

2.3D-3D: ICP
假设有一对匹配好的3D点：寻找一个欧氏变换R,t使,这个问题使用迭代最近点ICP求解。ICP的求解有两种方式：线性代数的求解(SVD),非线性优化方式(BA).
2.1SVD方法的一般步骤如下：
a.计算两组点的质心位置p,p',然后计算每个点的去质心坐标：
b.根据以下优化问题计算旋转矩阵：.
c.根据第二步的R,计算t:.
2.2非线性优化方法：以迭代方式寻找最优值
以李代数表达位姿时，目标函数可以写成，使用李代数扰动模型得到：。不断迭代找到极小值。具体BA的求解参考https://blog.csdn.net/xranmail/article/details/86486759.

3.李群李代数参考(https://blog.csdn.net/xiaocainiaodeboke/article/details/75041547)
使用2.2中非线性优化方法求解ICP问题时,需用李代数表达位姿。使用重投影计算位姿的表达式为：
.Pi是3D点, ui是Pi对应的像素位置, K为相机内参矩阵,si为ui对应的深度值。直接对上式求导无法解出,因为 T满足以下约束：R为旋转矩阵,它是正交矩阵并且行列式为1,t是平移向量。在求解T的时候,必须考虑到T满足的约束,那么这个问题就变成了有约束优化问题.可以去另外一个空间求解,比如李代数,可以将位姿表达式转化为无约束问题,然后很方便的通过GN法\LM法等优化算法求解。
3.1 群:一种集合加上一种运算的代数结构，把集合记为A，运算记为 .，群可以记为G=(A,.)
群要求这个运算要满足封闭性,结合律,幺元和可逆。矩阵中常见的群有：a.一般线性群GL(n):指n×n的可逆矩阵,它们对矩阵乘法成群;b.特殊正交群SO(n):就是旋转矩阵群,其中SO(2),SO(3)最为常见;c.特殊欧式群SE(n):就是n维欧式变换,其中SE(2),SE(3)最为常见。群结构保证了在群上的运算具有良好的性质,李群是指具有连续性质的群。SO(n),SE(n)在实数空间上是连续的,可以直观的感觉到一个刚体能够在空间中连续运动,所以SO(n)和SE(n)都是李群。那么相机的位姿就可以表示为：
这里说明了相机位姿是特殊欧式群，旋转矩阵是特殊正交群。
3.2李群和李代数相互转化
    
3.3 李代数的求导
使用李代数解决问题的求导思路分为两种：
step 1. 用李代数表示位姿,然后根据李代数加法来对李代数求导.
step 2. 对李群左乘或者右乘微小扰动量,然后对该扰动求导,成为左扰动和右扰动模型.
step1: 首先关于旋转矩阵对应的李代数SO(3)求导，第一种的求导过程，如下：

这样就得到了旋转后点相对于李代数的导数：,由于旋转矩阵对应的李代数是一个三维向量,所以我们可以用模长与单位向量的乘积表示。ϕ=θa, θ为模长,a为单位向量。
附：f(x)的导数为
step 2.接下来计算旋转矩阵李代数的左扰动模型,左乘一个微小扰动,对微小扰动求导：

,这种方式省去了计算雅克比Jl,
使用左扰动模型SE(3)上的李代数求导如下: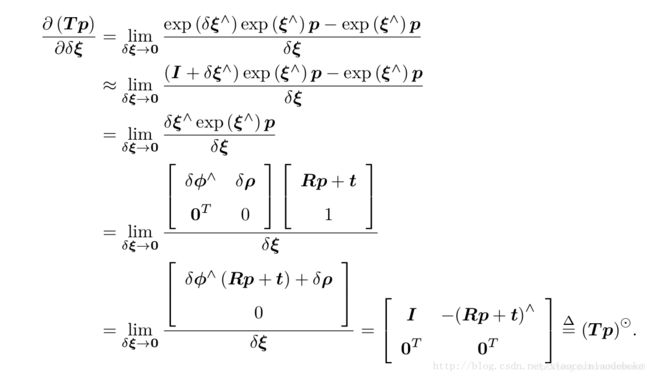

有了李群和李代数相互转换公式，李代数上的导数，那么我们就可以将位姿求解公式用李代数重新表达如下：
，对这个式子使用左扰动模型，利用链式法则展开：

相机投影模型相对于P‘为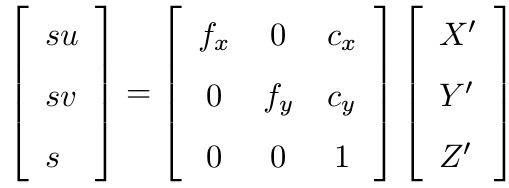：，消去s后，
得到，求导的第二项前面已经给出，取出这部分的前三行，然后两个导数项相乘，就可以得到一个2*6的雅克比矩阵：
。如果变换矩se(3)的旋转在前，平移在后，只需要将上式的前面3列和后面3列对调即可。有了李代数表示,下一步可以利用一些优化库(ceres,g2o)计算。