堆排序(heap sort)算法讲解与实现

堆排序(heap sort)算法讲解

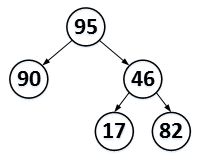
开始时，堆不可能是这个样子，因为，将数组转化为树，是有规则的，必须把左边填满才能再填右边。

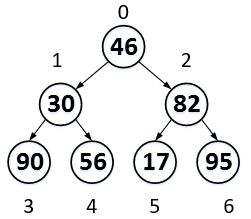
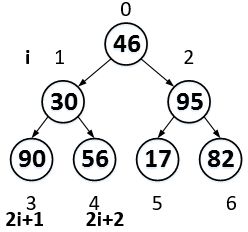
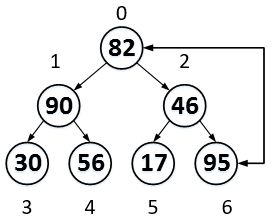
待排序数组：a = [46,30,82,90,56,17,95],组成一个二叉树，将46,30,82,90,56,17,95这几个数字从存储在数组结构，转变到二叉树及结构，是通过为一些数组下标赋予一些新的关系。比如，在数组中索引0和2的关系是，2是0的后两个元素，而在二叉树中，2是0的右子树。

第一步，将这样一个二叉树转化为堆。堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

从二叉树的倒数第二层的最右边开始，之所以从最右边，是因为我们在程序实现的时候，都是左节点和右节点比较，如果右节点比左节点大且比双亲节点大，则将右节点与双亲节点交换。

如果不用程序，我们自己按照堆排序算法思想排序，那那从左边开始，或者从右边开始都可以，但是，如果是用程序实现，我们的程序最好按照统一的规则，这样有利于我们实现算法。而不是一会从最右边开始，一会从最左边开始，不是不能实现，而是不方便实现。

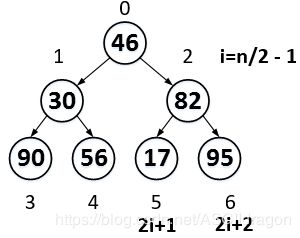
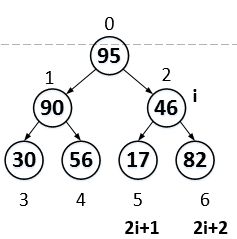
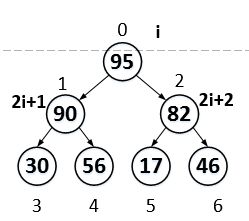
初始化i=n/2-1，注意：n是数组长度。

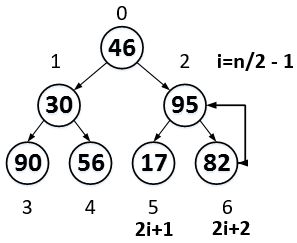
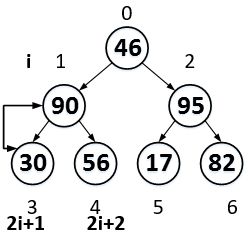
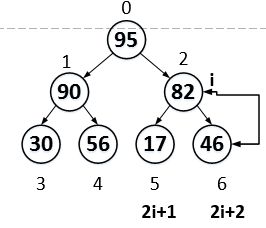
比较2i+1和2i+2，将其中比较大的一个与a[i]交换，也就是与父节点交换。由于95>17,95>82，所以，95和82互换。

 

移动以后的结果如上图所示。

 

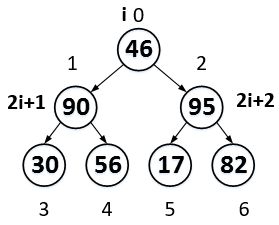
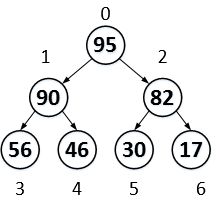
然后i-1，比较2i+1和2i+2，将较大的元素的索引值赋值给l，如果a[l] > a[i]，则将a[l]与a[i]交换。

交换以后的结果如上图所示。

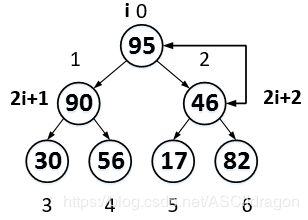
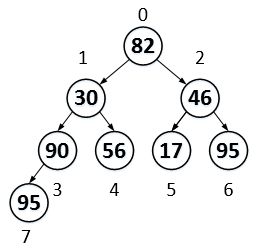
然后i-1，比较a[2i+1]和a[2i+2],将较大的数的索引下标赋值给l，记录下来，然后a[l]，也就是如果子节点中较大的一个大于父节点，则将其与父节点交换。

此时，95的右边子树又被打乱了。

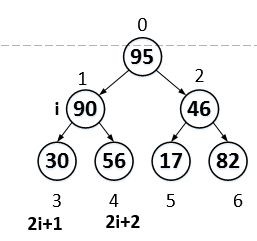
继续移动i，让i指向46这棵子树，然后调整这棵树。

交换后，结果如上图所示。

然后i-1，指向95的左节点，调整该子树。由于该子树本来满足堆的条件，所以不用调整。

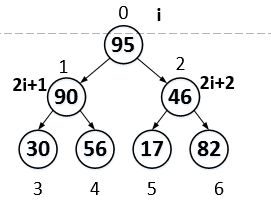
然后继续i-1，指向95，也不用调整。95大于两个子节点90和46，所以也不用调整。

此时，你会发现，每一个节点都大于等于其左右孩子的值，我们就完成了从一个二叉树到堆的转变。

当然，这只是准备工作，我们的目标是排序，不是构造堆。

将最后一个节点，也就是a[6]，与a[0]做交换，然后，此时i指针只需要从上向下调整一遍即可。但是调整时不再考虑a[6]，就当树里没有a[6]。

注意：是从上到下，不是从下到上。

 

我们得到了上图

我们对a[5],a[4],a[3],a[2],a[1]依次执行上述操作，也就是从前到后，每次跟变换以后新得到的a[0]交换。

最终我们得到了上图结果，此时a[0]到a[6]为一个依次递增序列。

算法在第二个阶段的特点是：

子顶向下调整

第i次循环根结点与n-i结点交换位置（n为节点数），并且，在调整过程中，不考虑移动下来的根结点。

代码详解

	for (i = n / 2 - 1; i >= 0; i--)

这句话里i = n/2-1表示从最后一个非叶子节点开始调整。

如果你的树是tree1这样的，倒数第二层最后一个节点没孩子即a[2]，那么，n/2 - 1  = 1,也就是，当下标2没有孩子，指针不会从下标2开始，因为它没有孩子，不需要调整。

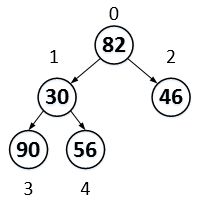tree1

但如果a[2]只有一个孩子，如tree2，n/2-1 = 2，指针都会从下标2开始，因为a[2]是有孩子，所以，我个人认为，这句话非常有意思

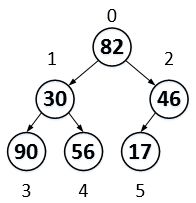tree2

这个图从a[3]开始调整，而不是a[2]

	for (; l <= end; c = l, l = 2 * l + 1)//将c设置为其左孩子，l设置为右孩子

l是当前所在下标，end是最后一个节点下标，l<=end，说明l还有孩子节点，则进入循环；如果l已经没有孩子节点了，则不再进入循环。

if (l < end && a[l] < a[l + 1])//如果右孩子小于end，并且,右孩子小于左孩子

这里l

 

c++实现代码

/*a为待排序数组，start为0，end为length(a)-1,改函数用于执行构建堆*/
void maxheap_down(int a[], int start, int end)
{
	int c = start;         
	int l = 2 * c + 1;//start的左孩子索引
	int tmp = a[c];            
	for (; l <= end; c = l, l = 2 * l + 1)//将c设置为其左孩子，l设置为右孩子
	{
		if (l < end && a[l] < a[l + 1])//如果右孩子小于end，并且,右孩子小于左孩子
			l++;       //将l改为左孩子索引
		if (tmp >= a[l])//如果c的孩子中较大的元素大于父亲节点
			break;   //则跳出循环
		else           //否则
		{
			a[c] = a[l];//将父亲节点和比自己大的孩子结点交换
			a[l] = tmp;
		}
	}
}

/*a为待排序数组，n为length(a)*/
void heap_sort_asc(int a[], int n)
{
	int i;
	for (i = n / 2 - 1; i >= 0; i--)
		maxheap_down(a, i, n - 1);
	for (i = n - 1; i > 0; i--)//设置n-1次循环，因为当n-1个节点都按顺序排好以后，最后一个一定是最小值
	{
		swap(a[0], a[i]);
		maxheap_down(a, 0, i - 1);
	}
}

参考博客：

算法思想：https://www.cnblogs.com/chengxiao/p/6129630.html

代码实现：https://www.cnblogs.com/skywang12345/p/3602162.html