【机器学习算法笔记系列】朴素贝叶斯(NB)算法详解和实战
朴素贝叶斯(NB)算法概述
朴素贝叶斯(Naïve Bayes, NB)算法,是一种基于贝叶斯定理与特征条件独立假设的分类方法。朴素:特征条件独立;贝叶斯:基于贝叶斯定理。属于监督学习的生成模型,实现简单,并有坚实的数学理论(即贝叶斯定理)作为支撑。在大量样本下会有较好的表现,不适用于输入向量的特征条件有关联的场景。
朴素贝叶斯算法原理
贝叶斯定理
- 条件概率:就是事件 A A A在另外一个事件 B B B已经发生条件下的发生概率。条件概率表示为 P ( A ∣ B ) P(A|B) P(A∣B),读作“在 B B B发生的条件下 A A A发生的概率”。
- 联合概率:表示两个事件共同发生(数学概念上的交集)的概率。 A A A与 B B B的联合概率表示为联合概率。 p ( A B ) p(AB) p(AB)
P ( A B ) = P ( A ∣ B ) P ( B ) = P ( B ∣ A ) P ( A ) , 若 A B 相 互 独 立 , P ( A B ) = P ( A ) P ( B ) P(AB)=P(A|B)P(B)=P(B|A)P(A),若AB相互独立,P(AB)=P(A)P(B) P(AB)=P(A∣B)P(B)=P(B∣A)P(A),若AB相互独立,P(AB)=P(A)P(B) - 全概率公式: P ( X ) = ∑ k P ( X ∣ Y = Y k ) P ( Y k ) , 其 中 ∑ k P ( Y k ) = 1 P(X)=\sum _kP(X|Y=Y_k)P(Y_k),其中\sum _kP(Y_k)=1 P(X)=∑kP(X∣Y=Yk)P(Yk),其中∑kP(Yk)=1
贝叶斯定理:贝叶斯理论是以18世纪的一位神学家托马斯.贝叶斯(Thomas Bayes)命名。通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A(发生)的条件下的概率是不一样的。然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
朴素贝叶斯:朴素贝叶斯方法是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布;然后基于此模型,对给定的输入 x x x,利用贝叶斯定理求出后验概率最大的输出 y y y:
P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x j ∣ Y = c k ) P(X=x| Y=c_{k})=P(X^{(1)=}x^{(1)},...,X^{(n)=}x^{(n)}|Y=c_k)=\prod_{j=1}^{n}P(X^{(j)}=x^{j}|Y=c_k) P(X=x∣Y=ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=ck)=j=1∏nP(X(j)=xj∣Y=ck)
朴素贝叶斯算法原理:其实朴素贝叶斯方法是一种生成模型,对于给定的输入 x x x,通过学习到的模型计算后验概率分布 P ( Y = c k ∣ X = x ) P(Y=c_k | X=x) P(Y=ck∣X=x),将后验概率最大的类作为 x x x的类输出。其中后验概率计算根据贝叶斯定理进行:
P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) P(Y=c_{k}|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_k P(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}|Y=c_k) } P(Y=ck∣X=x)=∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(X=x∣Y=ck)P(Y=ck)
然后,最后的朴素贝叶斯分类模型为:
y = f ( x ) = a r g m a x c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) y=f(x)=arg max_{c_k}\frac{P(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}|Y=c_k) } y=f(x)=argmaxck∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)
高斯贝叶斯分类器(GaussianNB)
在高斯朴素贝叶斯中,每个特征都是连续的,并且都呈高斯分布。高斯分布又称为正态分布。 GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布:
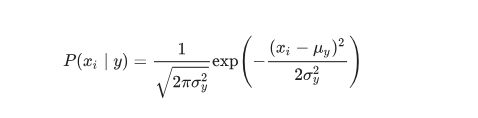
多项式贝叶斯分类器(MultinomialNB)
MultinomialNB 实现服从多项分布数据的贝叶斯算法,是一个经典的朴素贝叶斯在文本分类中使用的变种(其中的数据是通常表示为词向量的数量,虽然TF-IDF向量在实际项目中表现得很好),对于每一个 y y y来说,分布通过向量 Θ y = ( Θ y 1 , . . . , Θ y n ) \Theta_y=(\Theta_{y1},...,\Theta_{yn}) Θy=(Θy1,...,Θyn)参数化, n n n是类别的数目(在文本分类中,表示词汇量的长度), Θ y i \Theta_{yi} Θyi 表示标签 i i i出现的样本属于类别 y y y的概率 P ( x i ∣ y ) P(x_i|y) P(xi∣y)。
该参数 Θ y i \Theta_{yi} Θyi是一个平滑的最大似然估计,即相对频率计数:
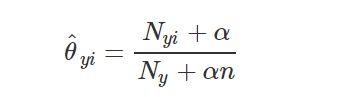
N y i = ∑ x ∈ T x i N_{yi}=\sum_{x\in T}x_i Nyi=∑x∈Txi:表示标签 i i i在样本集 T T T中属于类别 y y y的数目; N y = ∑ i = 1 ∣ T ∣ N y i N_{y}=\sum_{i=1}^{|T|}N_yi Ny=∑i=1∣T∣Nyi:表示在所有标签中类别 y y y出现的数目。
- 先验平滑参数 α ⩾ 0 \alpha \geqslant 0 α⩾0表示学习样本中不存在的特征并防止在计算中概率为0
- α = 1 \alpha=1 α=1被称为拉普拉斯平滑(Lapalce smoothing)
- α < 1 \alpha<1 α<1称为利德斯通平滑(Lidstone smoothing)
伯努利贝叶斯分类器(BernoulliNB)
BernoulliNB 实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法,即有多个特征,但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。 因此,这类算法要求样本以二元值特征向量表示;如果样本含有其他类型的数据, 一个 BernoulliNB 实例会将其二值化(取决于 binarize 参数)。
伯努利朴素贝叶斯的决策规则:
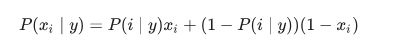
与多项分布朴素贝叶斯的规则不同 伯努利朴素贝叶斯明确地惩罚类 y y y中没有出现作为预测因子的特征 i i i,而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。
在文本分类的例子中,词频向量(word occurrence vectors)(而非词数向量(word count vectors))可能用于训练和用于这个分类器。 BernoulliNB 可能在一些数据集上可能表现得更好,特别是那些更短的文档。 如果时间允许,建议对两个模型都进行评估。
算法优缺点
优点
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点
- 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。
- 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
- 由于是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
- 对输入数据的表达形式很敏感。
Python实践
高斯贝叶斯分类器
其原型为:sklearn.naive_bayes.GaussianNB。sklearn.naive_bayes.GaussianNB
参数
GaussianNB没有参数,因此不需要调参。
属性
class_prior_:一个数组,形状为(n_classes,),是每个类别的概率。
class_count_:一个数组,形状为(n_classes,),是每个类别包含的训练样本数量。
theta_:一个数组,形状为(n_classes, n_features),是每个类别上每个特征的均值 u k u_k uk。
sigma_:一个数组,形状为(n_classes, n_features),是每个类别上每个特征的标准差 δ k \delta _{k} δk。
方法
fit(X, y[, sample_weight]):训练模型。
partial_fit(X, y[, classes, sample_weight]):追加训练数据。该方法主要用于大规模数据集的训练。此时可以将大数据集划分成若干个小数据集,然后在这些小数据集上连续调用partial_fit方法来训练模型。
predict(X):用模型进行预测,返回预测值。
predict_log_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值。
predict_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率值。
score(X, y[, sample_weight]):返回在(X, y)上预测的准确率(accuracy)。
多项式贝叶斯分类器
其原型为:sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)。sklearn.naive_bayes.MultinomialNB
参数
alpha:float,指定 α \alpha α值。
fit_prior:bool,如果为True,则不去学习 P ( y = c k ) P(y=c_k) P(y=ck),替代以均匀分布;如果为False,则去学习 P ( y = c k ) P(y=c_k) P(y=ck)。
class_prior:一个数组。它指定每个分类的先验概率 P ( y = c 1 ) , P ( y = c 2 ) , . . . , P ( y = c k ) P(y=c_1),P(y=c_2),...,P(y=c_k) P(y=c1),P(y=c2),...,P(y=ck)。如果指定了该参数,则每个分类的先验概率不再从数据集中学得。
属性
class_log_prior:一个数组,形状为(n_classes,)。给出每个类别调整后的经验概率分布的对数值。
feature_log_prior:一个数组,形状为(n_classes, n_features)。给出了 P ( X ( j ) ∣ y = c k ) P(X^{(j)}|y=c_k) P(X(j)∣y=ck)的经验概率分布的对数值。
class_count_:一个数组,形状为(n_classes,)。是每个类别包含的训练样本数量。
feature_count_:一个数组,形状为(n_classes, n_features)。训练过程中,每个类别每个特征遇到的样本数。
方法
fit(X, y[, sample_weight]):训练模型。
partial_fit(X, y[, classes, sample_weight]):追加训练数据。该方法主要用于大规模数据集的训练。此时可以将大数据集划分成若干个小数据集,然后在这些小数据集上连续调用partial_fit方法来训练模型。
predict(X):用模型进行预测,返回预测值。
predict_log_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值。
predict_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率值。
score(X, y[, sample_weight]):返回在(X, y)上预测的准确率(accuracy)。
伯努利贝叶斯分类器
其原型为:sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True)。sklearn.naive_bayes.BernoulliNB
参数
alpha:float,指定 α \alpha α值。
binarize:一个浮点数或者None。
- 如果为None,那么会假定原始数据已经二元化了。
- 如果是
float,那么会以该数值为界,特征取值大于它的作为1;特征值小于它的作为0。采取这种策略来二元化。
fit_prior:bool,如果为True,则不去学习 P ( y = c k ) P(y=c_k) P(y=ck),替代以均匀分布;如果为False,则去学习 P ( y = c k ) P(y=c_k) P(y=ck)。
class_prior:一个数组。它指定每个分类的先验概率 P ( y = c 1 ) , P ( y = c 2 ) , . . . , P ( y = c k ) P(y=c_1),P(y=c_2),...,P(y=c_k) P(y=c1),P(y=c2),...,P(y=ck)。如果指定了该参数,则每个分类的先验概率不再从数据集中学得。
属性
class_log_prior:一个数组,形状为(n_classes,)。给出每个类别调整后的经验概率分布的对数值。
feature_log_prior:一个数组,形状为(n_classes, n_features)。给出了 P ( X ( j ) ∣ y = c k ) P(X^{(j)}|y=c_k) P(X(j)∣y=ck)的经验概率分布的对数值。
class_count_:一个数组,形状为(n_classes,)。是每个类别包含的训练样本数量。
feature_count_:一个数组,形状为(n_classes, n_features)。训练过程中,每个类别每个特征遇到的样本数。
方法
fit(X, y[, sample_weight]):训练模型。
partial_fit(X, y[, classes, sample_weight]):追加训练数据。该方法主要用于大规模数据集的训练。此时可以将大数据集划分成若干个小数据集,然后在这些小数据集上连续调用partial_fit方法来训练模型。
predict(X):用模型进行预测,返回预测值。
predict_log_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值。
predict_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率值。
score(X, y[, sample_weight]):返回在(X, y)上预测的准确率(accuracy)。
朴素贝叶斯算法实战—英文文档分类
朴素贝叶斯算法在自然语言处理领域有广泛的应用,也是最早用于文本分类的算法之一。因此,实战环节,我们采用文本分类的例子。此示例中使用的数据集是20Newsgroups-18828版本。
20Newsgroups数据集是用于文本分类、文本挖据和信息检索研究的国际标准数据集之一。数据集收集了大约20,000左右的新闻组文档,均匀分为20个不同主题的新闻组集合。
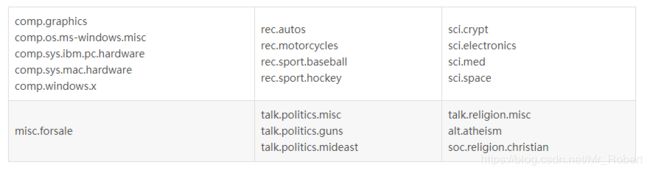
20newsgroups数据集有三个版本。第一个版本19997是原始的并没有修改过的版本。第二个版本是按时间顺序分为训练(60%)和测试(40%)两部分数据集,不包含重复文档和新闻组名(新闻组,路径,隶属于,日期)。第三个版本18828不包含重复文档,只有来源和主题。
- 20news-19997.tar.gz –原始20 Newsgroups数据集
- 20news-bydate.tar.gz –按时间分类; 不包含重复文档和新闻组名(18846 个文档)
- 20news-18828.tar.gz– 不包含重复文档,只有来源和主题 (18828 个文档)
我们将使用train子目录下的文档进行模型训练,然后使用test子目录下的文档进行模型测试。
首先,我们加载数据来查看数据:
__author__ = "fpZRobert"
"""
20Newsgroup英文文本分类
"""
from sklearn.datasets import load_files
"""
加载数据
"""
print("加载训练数据!!!")
news_train = load_files("./data/train")
print("Train Summary: {0} documents in {1} categories.".format(len(news_train.data), len(news_train.target_names)))
print("加载测试数据!!!")
news_test = load_files("./data/test")
print("Test Summary: {0} documents in {1} categories.".format(len(news_test.data), len(news_test.target_names)))
Out:
加载训练数据!!!
Train Summary: 13180 documents in 20 categories.
加载测试数据!!!
Test Summary: 5648 documents in 20 categories.
我们可以看到,train和test子目录下包含20个子目录,每个子目录代表一种文档的类型,文档类型上述表格已给出。子目录下的所有文档都是属于该子目录的文档类型,即类别。训练集一共13180篇文档,测试集一共5648篇文档。读者可以自行下载浏览数据,以便更加清楚认识数据集。例如train/sci.crypt/10629-15886是一个讨论芯片的帖子:
From: [email protected] (David Koontz )
Subject: Re: How to make the Clipper chip and wiretapping less bad
What is the reason for the push on clipper?
Two days after the lead story here in the Mercury Times (murky news)
there was another article on industrial espionage by the french.
Someone had said what can it hurt to allow the government to have
continued access to our communications, they already have it. The
problem is that, yes the do have access, and probably more than
we realize. The government wants exclusive access to communications
intercept here in the united states, cutting out other access detrimental
to the national security (tm).
I also doubt that a certain3 letter agency, that originated the encryption
algorithm and the chip designs needs to have anything to do with the
escrow system to continue their intercept effort.
Better yet, who owns the company doing the programming?
不管是中文文档,还是英文文档,都需要将文档表达为计算机可以理解并处理的信息,这是自然语言处理中一个很重要的课题。英文文档相较于中文文档来说,不需要进行分词,这是其最大区别。本文简单介绍TF-IDF的原理,以便更好理解本文实例。
TF-IDF
TF-IDF(Term Frequency-Inverse Document Frequency, 词频-逆文件频率), TF-IDF是一种统计方法,用来评估一个词语对一篇文档的重要程度。词语的重要性随着它在文档中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。
词频 (term frequency, TF):指的是某个特定的词语在该文档中出现的次数。

逆向文件频率 (inverse document frequency, IDF) :主要思想是:如果包含词条 t t t的文档越少, IDF越大,则说明词条具有很好的类别区分能力。
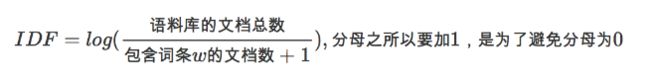
某一特定文档内的高频词语,以及该词语在整个文档集合中的低文档频率,可以产生出高权重的TF-IDF。因此,TF-IDF倾向于过滤掉常见的词语,保留重要的词语。
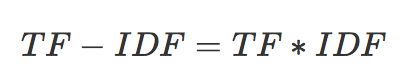
OK,回归主线,有了TF-IDF工具,我们就可以把一篇文档转换成一个向量。首先,可以从数据集(自然语言处理领域也称为corpus,即语料库)里提取出所有出现的词语,我们称之为词典。假设词典中共有50000个词,则每篇文档都可转换为一个50000维的向量。其次,针对每篇文档中出现的词,都要计算其TF-IDF的值,并把这个值填入文档向量里这个词对应的位置上。这样就完成了一篇文档到一个向量的转换过程,而向量计算机就可以处理了。一篇文档往往只会由词典里的一小部分词构成,这就意味着这个向量里的大部分元素都是0。
上述过程不需要我们自己写代码去完成,scikit-learn软件包里实现了把文档转换为向量的过程,这里我们只需知道如何调用即可。
上述代码已经完成语料库读入内存的操作。load_files()函数会从这个目录里把所有的文档都读入内存,并且自动根据所在的子目录名称打上标签。其中,news_train.data 是一个数组,包含所有训练文档的文本信息。 news_train.target也是一个数组,包含所有训练文档的类别,而news_train.target_names则是类别的名称,测试集类似,这里不再重复叙述。
训练语料库中共有13180篇文档,测试语料库中共有5648篇文档,其中分成20个类别。接着,需要把这些文档全部转换为由TF-IDF表达的权重信息构成的向量:
"""
文档的数字表达
"""
from sklearn.feature_extraction.text import TfidfVectorizer
print("训练数据向量化!!!")
vectorizer = TfidfVectorizer(encoding="latin-1")
X_train = vectorizer.fit_transform((d for d in news_train.data))
y_train = news_train.target
print("train_n_samples: %d, train_n_features: %d" % X_train.shape)
Out:
训练数据向量化!!!
train_n_samples: 13180, train_n_features: 130274
TFidfVectorizer类是用来将所有的文档转换为矩阵,该矩阵每行代表一篇文档,一行中每个元素代表一个对应的词的重要性,词的重要性由TF-IDF表示。熟悉scikit-learn API的读者应该清楚,其fit_transform()方法是fit()和transform()合并起来的。其中,fit()会先完成语料库分析、提取词典等操作,transform()会把每篇文档转换为向量,最终构成矩阵,保存在X_train变量里。由输出可以看出,词典一共包含130274个词,即每篇文档都转换为一个130274维的向量。
终于把文档数据转换为scikit-learn里典型的训练数据集矩阵了,矩阵每一行表示为一个数据样本,每一列表示为一个特征。我们使用MultinomialNB对数据集进行训练:
"""
模型训练
"""
from sklearn.naive_bayes import MultinomialNB
print("模型训练中!!!")
clf = MultinomialNB(alpha=0.0001)
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)
print("train score: {0}".format(train_score))
其中,alpha表示为平滑参数,其值越小,越容易造成过拟合;值越大,容易造成欠拟合。笔者计算机上的输出为:
模型训练中!!!
train score: 0.9978755690440061
为了判断我们训练的模型是否可用,需要对模型进行评价,首先,我们将测试集文档也转换为向量:
print("测试数据向量化!!!")
X_test = vectorizer.transform((d for d in news_test.data))
y_test = news_test.target
print("test_n_samples: %d, test_n_features: %d" % X_test.shape)
Out:
测试数据向量化!!!
test_n_samples: 5648, test_n_features: 130274
这里需要注意,vectorizer变量是我们处理训练集时用到的向量化的类的实例,此处我们只需要调用transform()进行TF-IDF数值计算即可,不需要再调用fit()进行语料库的分析了,这样可以保证训练集和测试集维度相同。
scikit-learn包提供了全方位的模型评价工具,首先对测试集进行预测,然后使用classification_report()函数来查看一下针对每个类别的预测准确性:
"""
模型测试
"""
print("模型测试!!!")
pred = clf.predict(X_test)
from sklearn.metrics import classification_report
print(classification_report(y_test, pred, target_names=news_test.target_names))
笔者计算机上的输出为:
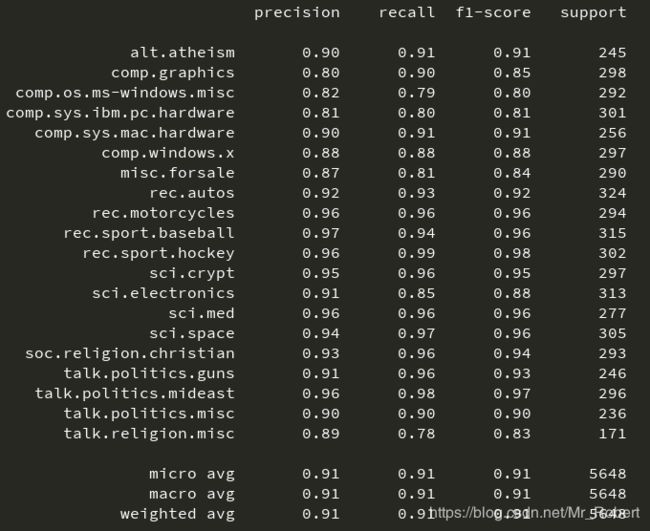
从输出结果看,针对每种类别都统计了查准率、召回率和F1-Score,这是文本分类常用评价指标。此外,还可以通过confusion_matrix()函数生成混淆矩阵,观察每种类别被错误分类的情况,由于本实验数据,类别众多,可能不能在一行显示:
"""
查看混淆矩阵
"""
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, pred)
print("Confusion Matrix:")
print(cm)
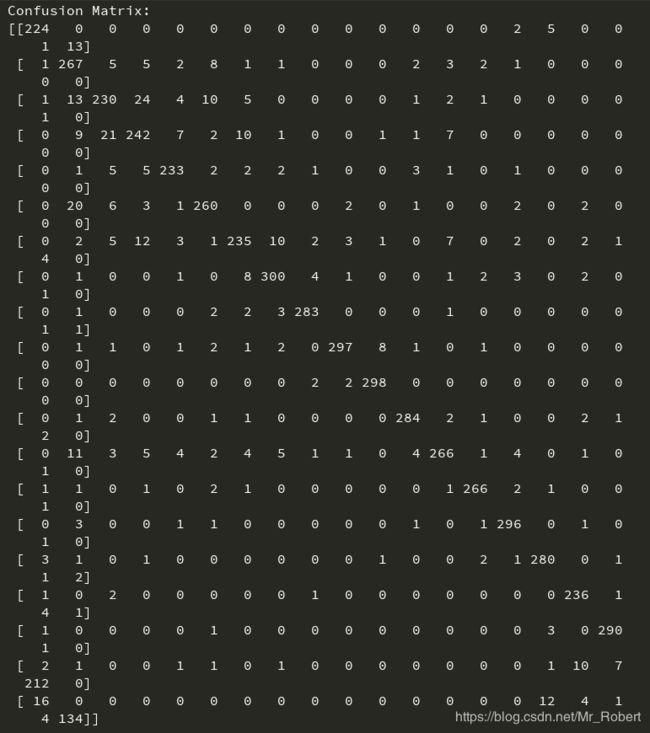
这种混淆矩阵,看着简直头皮发麻,我们通过数据可视化进行展示:
"""
混淆矩阵可视化
"""
import matplotlib.pyplot as plt
import seaborn as sn
sn.heatmap(cm, annot=True)
plt.show()
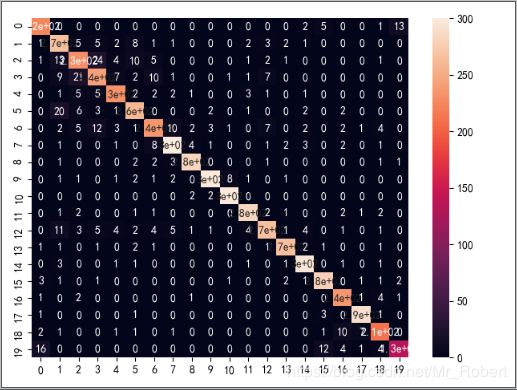
除对角线外,其他地方颜色越浅,说明此处错误越多。通过这些数据,我们可以详细分析样本数据,进一步优化模型。可能会有读者很纳闷,下载的数据集中还有验证集,本文并没有叙述,其实,本文朴素贝叶斯分类器alpha是个超参数,需要通过实验,选择最合适的参数,读者可以自己利用验证集进行调试。
全部代码:
__author__ = "fpZRobert"
"""
20Newsgroup英文文本分类
"""
from sklearn.datasets import load_files
"""
加载数据
"""
print("加载训练数据!!!")
news_train = load_files("./data/train")
print("Train Summary: {0} documents in {1} categories.".format(len(news_train.data), len(news_train.target_names)))
print("加载测试数据!!!")
news_test = load_files("./data/test")
print("Test Summary: {0} documents in {1} categories.".format(len(news_test.data), len(news_test.target_names)))
"""
文档的数字表达
"""
from sklearn.feature_extraction.text import TfidfVectorizer
print("训练数据向量化!!!")
vectorizer = TfidfVectorizer(encoding="latin-1")
X_train = vectorizer.fit_transform((d for d in news_train.data))
y_train = news_train.target
print("train_n_samples: %d, train_n_features: %d" % X_train.shape)
print("测试数据向量化!!!")
X_test = vectorizer.transform((d for d in news_test.data))
y_test = news_test.target
print("test_n_samples: %d, test_n_features: %d" % X_test.shape)
"""
模型训练
"""
from sklearn.naive_bayes import MultinomialNB
print("模型训练中!!!")
clf = MultinomialNB(alpha=0.0001)
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)
print("train score: {0}".format(train_score))
"""
模型测试
"""
print("模型测试!!!")
pred = clf.predict(X_test)
from sklearn.metrics import classification_report
print(classification_report(y_test, pred, target_names=news_test.target_names))
"""
查看混淆矩阵
"""
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, pred)
print("Confusion Matrix:")
print(cm)
"""
混淆矩阵可视化
"""
import matplotlib.pyplot as plt
import seaborn as sn
sn.heatmap(cm, annot=True)
plt.show()