卷积:如何成为一个很厉害的神经网络
转自知乎: https://zhuanlan.zhihu.com/p/25754846
原文:An Intuitive Explanation of Convolutional Neural Networks
作者:Ujjwal Karn
翻译:Kaiser(王司图)
动图+在线练习版本:卷积:如何成为一个很厉害的神经网络 - 集智专栏
前言
- 如果你对神经网络还是完全陌生的,建议阅读9行Python代码搭建神经网络来掌握一些基本概念。
- 本文含有部分gif动图,有可能无法播放,也需要访问上面的“集智”链接查看。
什么是卷积神经网络?又为什么很重要?
卷积神经网络(Convolutional Neural Networks, ConvNets or CNNs)是一种在图像识别与分类领域被证明特别有效的神经网络。卷积网络已经成功地识别人脸、物体、交通标志,应用在机器人和无人车等载具。
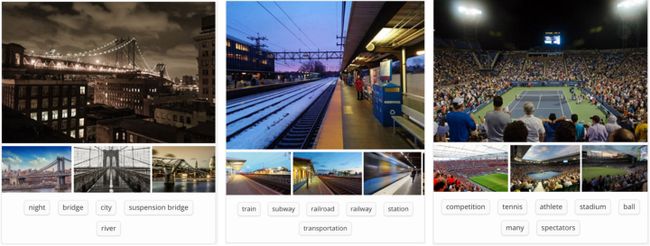
在上面的图1当中,卷积网络能够识别场景而系统可以自动推荐相关标签如“桥”、“铁路”、“网球”等。图2则展示了卷积网络识别日常事物如人、动物的例子。最近,卷积网络也已经在自然语言处理上显示出了威力(比如句子分类)。
卷积网络,在今天的绝大多数机器学习应用中都是极重要的工具。但是,理解卷积网络并首次学着使用,这体验有时并不友好。本文的主旨在于帮助读者理解,卷积神经网络是如何作用于图片的。
在本文,多层感知机(Multi-Layer Perceptrons, MLP)也被记作全连接层(Fully Connected Layers)。
LeNet架构(1990年代)
LeNet是最早用于深度学习了领域的卷积神经网络之一。Yann LeCun的这一杰作LeNet5得名于他自1988年以来的系列成功迭代。彼时LeNet架构还主要被用于识别邮政编码等任务。
下面我们将直观地感受一下,LeNet是如何学习识别图像的。近几年已经出现了很多建立在LeNet之上的新架构,但是基本概念还是来自于LeNet,并且理解了LeNet再学其他的也会更简单。
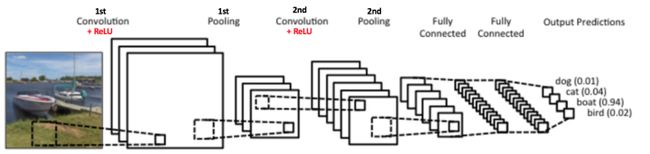
图3的卷积神经网络与LeNet的原始架构十分接近,把图片分入四个类别:狗,猫,船,鸟(LeNet最早主要就是用来做这些)。如上图所示,当获得一张船图作为输入的时候,网络正确的给船的分类赋予了最高的概率(0.94)。输出层的各个概率相加应为1.
图3的卷积神经网络主要执行了四个操作:
- 卷积
- 非线性(ReLU)
- 池化或下采样
- 分类(全连接层)
这些操作也是所有卷积神经网络的基石,所以理解好这些工作对于理解整个神经网络至关重要。接下来我们将尝试最直观地理解以上操作。
图片是像素值的矩阵
本质上来讲,每个图片都可以表示为像素值组成的矩阵:
通道是代指图片特定成分的习语。常见数码相机拍出来的照片有三个通道——红、绿、蓝-可以想象为是三个2d矩阵(每种颜色对应一个)叠在一起,每个矩阵的值都在0-255之间。
另一方面,灰度图像只有单通道。本文为简单起见只考虑灰度图像,这样就是一个2d矩阵。矩阵中的每个像素值还是0到255——0表示黑,255表示白。
卷积
卷积网络是因为“卷积”操作而得名的。卷积的根本目的是从输入图片中提取特征。卷积用一个小方阵的数据学习图像特征,可以保留像素之间的空间关系。这里不深入探讨卷积的数学原理,重在理解工作过程。
如上所述,每个图片都是像素值矩阵。考虑一个5x5的图像,其像素值为0和1,下面的绿色矩阵是灰度图的特例(常规灰度图的像素值取值0-255),同时考虑如下的3x3矩阵:
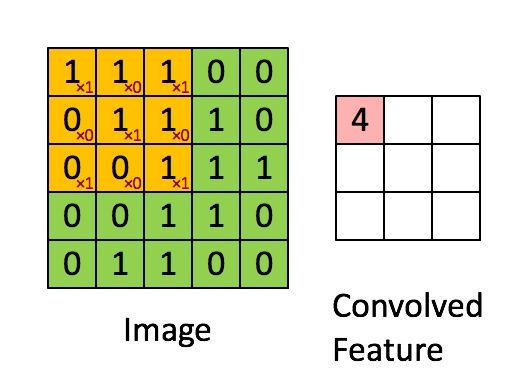
然后,5x5图像和3x3矩阵之间的卷积计算,可由下图的动画所表示:
图5:卷积操作。输出矩阵叫卷积特征或特征映射
想一想以上操作是如何完成的,我们在原始图片(绿色)上1像素、1像素地滑动橙色矩阵(也称'stride'),并且在每个位置上,我们都对两个矩阵的对应元素相乘后求和得到一个整数,这就是输出矩阵(粉色)的元素。注意,3x3矩阵每次只“看见”输入图片的一部分。
3x3矩阵也叫“滤波器”、“核”或“特征探测器”,在原图上滑动滤波器、点乘矩阵所得的矩阵称为“卷积特征”、“激励映射”或“特征映射”。这里的重点就是,理解滤波器对于原输入图片来说,是个特征探测器。
对于同一张照片,不同的滤波器将会产生不同的特征映射。比如考虑下面这张输入图片:
下表可见各种不同卷积核对于上图的效果。只需调整滤波器的数值,我们就可以执行诸如边缘检测、锐化、模糊等效果——这说明不同的滤波器会从图片中探测到不同的特征,比如边缘、曲线等。
另一种对卷积操作很好的理解方式就是观察图6的动画:
(gif体积过大,无法上传)
一个滤波器(红框)在图片上滑动(卷积)产生特征映射。在同一个图片上,另一个滤波器(绿框)的卷积产生了不同的特征映射。须知,卷积操作捕捉的是原图的局部依赖性。另外,注意观察两个不同的滤波器怎样产生不同的特征映射。其实不管是图片,还是两个滤波器,本质上都不过是我们刚才看过的数值矩阵而已。
在实践当中,卷积神经网络在训练过程中学习滤波器的值,当然我们还是要在训练之前需要指定一些参数:滤波器的个数,滤波器尺寸、网络架构等等。滤波器越多,从图像中提取的特征就越多,模式识别能力就越强。
特征映射的尺寸由三个参数控制,我们需要在卷积步骤之前就设定好:
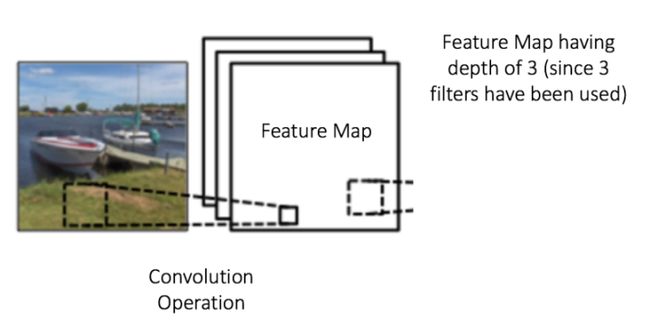
- 深度(Depth): 深度就是卷积操作中用到的滤波器个数。如图7所示,我们对原始的船图用了三个不同的滤波器,从而产生了三个特征映射。你可以认为这三个特征映射也是堆叠的2d矩阵,所以这里特征映射的“深度”就是3。
-
步幅(Stride):步幅是每次滑过的像素数。当Stride=1的时候就是逐个像素地滑动。当Stride=2的时候每次就会滑过2个像素。步幅越大,特征映射越小。
-
补零(Zero-padding):有时候在输入矩阵的边缘填补一圈0会很方便,这样我们就可以对图像矩阵的边缘像素也施加滤波器。补零的好处是让我们可以控制特征映射的尺寸。补零也叫宽卷积,不补零就叫窄卷积。
非线性
如图3所示,每个卷积操作之后,都有一个叫ReLU的附加操作。ReLU的全称是纠正线性单元(Rectified Linear Unit),是一种非线性操作,其输出如下:
图8:ReLU
ReLU是以像素为单位生效的,其将所有负值像素替换为0。ReLU的目的是向卷积网络中引入非线性,因为真实世界里大多数需要学习的问题都是非线性的(单纯的卷积操作时线性的——矩阵相乘、相加,所以才需要额外的计算引入非线性)。
图9可以帮助我们清晰地理解,ReLU应用在图6得到的特征映射上,输出的新特征映射也叫“纠正”特征映射。(黑色被抹成了灰色)
图9:ReLU
其他非线性方程比如tanh或sigmoid也可以替代ReLU,但多数情况下ReLU的表现更好。
池化
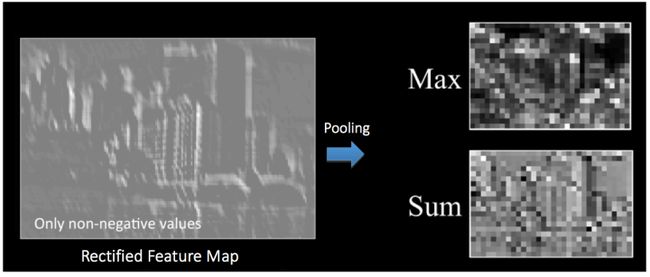
空间池化(也叫亚采样或下采样)降低了每个特征映射的维度,但是保留了最重要的信息。空间池化可以有很多种形式:最大(Max),平均(Average),求和(Sum)等等。
以最大池化为例,我们定义了空间上的邻域(2x2的窗)并且从纠正特征映射中取出窗里最大的元素。除了取最大值以额外,我们也可以取平均值(平均池化)或者把窗里所有元素加起来。实际上,最大池化已经显示了最好的成效。
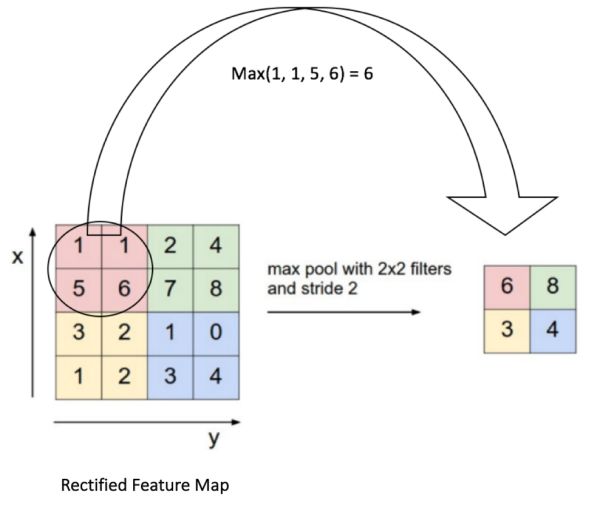
图10显示了对纠正特征映射的最大池化操作(在卷积+ReLU之后),使用的是2x2的窗。
我们以2格的步幅(Stride)滑动2x2的窗,并且取每个区域的最大值。图10同样显示了池化可以减少特征映射的维度。
在图11所示的网络中,池化操作分别应用于每个特征映射(注意正因如此,我们从三个输入映射得到了三个输出映射)。
图12即为池化操作施加在图9所得纠正特征映射上的效果。
池化的功能室逐步减少输入表征的空间尺寸。特别地,池化
- 使输入表征(特征维度)更小而易操作
- 减少网络中的参数与计算数量,从而遏制过拟合
- 增强网络对输入图像中的小变形、扭曲、平移的鲁棒性(输入里的微小扭曲不会改变池化输出——因为我们在局部邻域已经取了最大值/平均值)。
- 帮助我们获得不因尺寸而改变的等效图片表征。这非常有用,因为这样我们就可以探测到图片里的物体,不论那个物体在哪。
截至目前:
至此我们已经了解了卷积、ReLU和池化是如何运转的,这些层对于所有的卷积神经网络都是最基础的单元。如图13所示,我们有两组“卷积+ReLU+池化”层——其中第二组对第一组的输出施加了六个滤波器,产生了六个特征映射。ReLU分别作用域这六个特征映射,再对生成的纠正特征映射使用最大池化。
这些层合力提取出有用的特征,为网络引入了非线性并降低了维度,还使特征对尺寸和平移保持不变性。
第二个池化层的输出相当于全连接层的输入,我们将在下一节继续探讨。
全连接层
全连接层(Fully Connected layer)就是使用了softmax激励函数作为输出层的多层感知机(Multi-Layer Perceptron),其他很多分类器如支持向量机也使用了softmax。“全连接”表示上一层的每一个神经元,都和下一层的每一个神经元是相互连接的。
卷积层和池化层呢个的输出代表了输入图像的高级特征,全连接层的目的就是用这些特征进行分类,类别基于训练集。比如图14所示的图像分类任务,有四种可能的类别。(注意,图14没有显示出所有的神经元节点)
图14:全连接层——每个节点都与相邻层的所有节点相连
除了分类以外,加入全连接层也是学习特征之间非线性组合的有效办法。卷积层和池化层提取出来的特征很好,但是如果考虑这些特征之间的组合,就更好了。
全连接层的输出概率之和为1,这是由激励函数Softmax保证的。Softmax函数把任意实值的向量转变成元素取之0-1且和为1的向量。
联合起来——反向传播训练
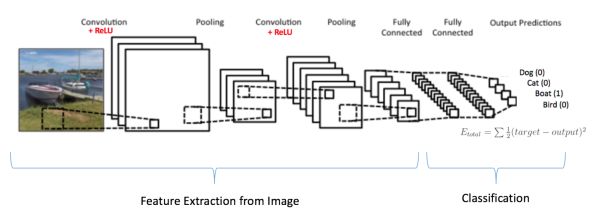
综上,卷积+池化是特征提取器,全连接层是分类器。
注意图15,因为输入图片是条船,所以目标概率对船是1,其他类别是0.
- 输入图像 = 船
- 目标向量 = [0, 0, 1 ,0]
图15:训练卷积神经网络
卷积网络的训练过程可以概括如下:
-
Step 2: 网络将训练图片作为输入,执行前向步骤(卷积,ReLU,池化以及全连接层的前向传播)并计算每个类别的对应输出概率。
- 假设船图的输出概率是[0.2, 0.4, 0.1, 0.3]
- 因为第一个训练样本的权重都是随机的,所以这个输出概率也跟随机的差不多
-
Step 3: 计算输出层的总误差(4类别之和)
- 总误差=∑12(目标概率−输出概率)2总误差=∑12(目标概率−输出概率)2
-
Step 4: 反向传播算法计算误差相对于所有权重的梯度,并用梯度下降法更新所有的滤波器/权重和参数的值,以使输出误差最小化。
- 权重的调整程度与其对总误差的贡献成正比。
- 当同一图像再次被输入,这次的输出概率可能是[0.1, 0.1, 0.7, 0.1],与目标[0, 0, 1, 0]更接近了。
- 这说明我们的神经网络已经学习着分类特定图片了,学习的方式是调整权重/滤波器以降低输出误差。
- 如滤波器个数、滤波器尺寸、网络架构这些参数,是在Step 1之前就已经固定的,且不会在训练过程中改变——只有滤波矩阵和神经元突触权重会更新。
以上步骤训练了卷积网络——本质上就是优化所有的权重和参数,使其能够正确地分类训练集里的图片。
当一个新的(前所未见的)的图片输入至卷积网络,网络会执行前向传播步骤并输出每个类别的概率(对于新图像,输出概率用的也是训练过的权重值)。如果我们的训练集足够大,网络就有望正确分类新图片,获得良好的泛化(generalization)能力。
注意 1: 以上步骤已被极大简化,且数学细节均以忽略,这是为了让训练过程更直观。
注意 2: 上例中,我们用了两组卷积+池化层,其实这些操作可以在一个卷积网络内重复无数次。如今有些表现出众的卷积网络,都有数以十计的卷积+池化层!并且,不是每个卷积层后面都要跟个池化层。由图16可见,我们可以有连续多组卷积+ReLU层,后面再加一个池化层。
图16可视化卷积神经网络
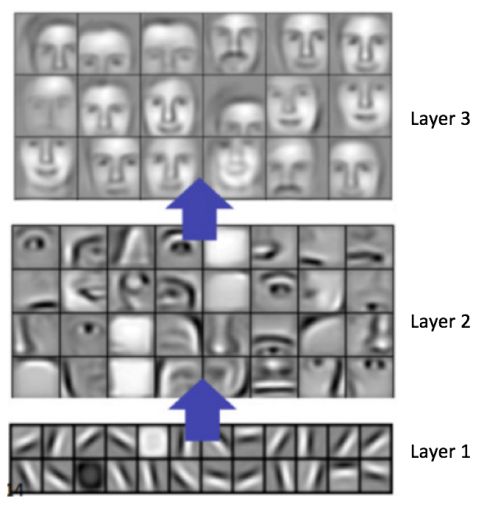
一般来说,卷积层越多,能学会的特征也就越复杂。比如在图像分类中,一个卷积神经网络的第一层学会了探测像素中的边缘,然后第二层用这些边缘再去探测简单的形状,其他层再用形状去探测高级特征,比如脸型,如图17所示——这些特征是Convolutional Deep Belief Network学得的。这里只是一个简单的例子,实际上卷积滤波器可能会探测出一些没有意义的特征。
图17:Convolutional Deep Belief Network学习的特征
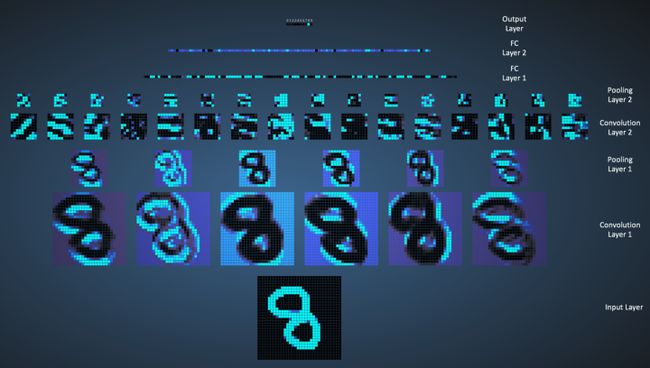
Adam Harley做了一个非常惊艳的卷积神经网络可视化,这个网络是用MNIST手写数字数据库训练而来的。我强烈推荐大家玩一玩,以便更深地理解卷积神经网络的细节。
如下我们将看到网络是如何识别输入数字"8"的。注意,图18没有把ReLU过程单独显示出来。
输入图像有1024个像素(32x32图片),第一个卷积层(Convolution Layer 1)有六个不同的5x5滤波器(Stride = 1)。由图可见,六个不同的滤波器产生了深度为6的特征映射。
Convolutional Layer 1 后面跟着Pooling Layer 1, 对六个特征映射分别进行2x2的最大池化(Stride = 2)。你可以在动态网页中的每个像素上活动鼠标指针,观察其在前一个卷积层里对应的4x4网格(如图19)。不难发现,每个4x4网格里的最亮的像素(对应最大值)构成了池化层。
图19:可视化池化操作
之后我们有三个全连接(FC)层:
- FC 1: 120神经元
- FC 2: 100神经元
- FC 3: 10神经元,对应10个数字——也即输出层
在图20,输出层10个节点中的每一个,都与第二个全连接层的100个节点相连(所以叫“全连接”)。
注意输出层里的唯一的亮点对应着8——这说明网络正确的识别了手写数字(越亮的节点代表越高的概率,比如这里8就拥有最高的概率)。
该可视化的3D版可见于这里。
其他卷积网络架构
卷积神经网络始自1990年代起,我们已经认识了最早的LeNet,其他一些很有影响力的架构列举如下:
-
1990s至2012:从90年代到2010年代早期,卷积神经网络都处于孵化阶段。随着数据量增大和计算能力提高,卷积神经网络能搞定的问题也越来越有意思了。
-
AlexNet(2012):2012年,Alex Krizhevsky发布了AlexNet,是LeNet的更深、更宽版本,并且大比分赢得了当年的ImageNet大规模图像识别挑战赛(ILSVRC)。这是一次非常重要的大突破,现在普及的卷积神经网络应用都要感谢这一壮举。
-
ZF Net(2013):2013年的ILSVRC赢家是Matthew Zeiler和Rob Fergus的卷积网络,被称作ZF Net,这是调整过架构超参数的AlexNet改进型。
-
GoogleNet(2014):2014的ILSVRC胜者是来自Google的Szegedy et al.。其主要贡献是研发了Inception Module,它大幅减少了网络中的参数数量(四百万,相比AlexNet的六千万)。
-
VGGNet(2014):当年的ILSVRC亚军是VGGNet,突出贡献是展示了网络的深度(层次数量)是良好表现的关键因素。
-
ResNet(2015): Kaiming He研发的Residual Network是2015年的ILSVRC冠军,也代表了卷积神经网络的最高水平,同时还是实践的默认选择(2016年5月)。
-
DenseNet(2016年8月): 由Gao Huang发表,Densely Connected Convolutional Network的每一层都直接与其他各层前向连接。DenseNet已经在五个高难度的物体识别基础集上,显式出非凡的进步。
(翻译部分 完)
经过本文和之前的系列文章,您应该已经掌握了卷积神经网络的基本原理。接下来我们尝试用流行的Python深度学习库Keras,动手实地搭建一个LeNet。
实践是神经网络的唯一标准
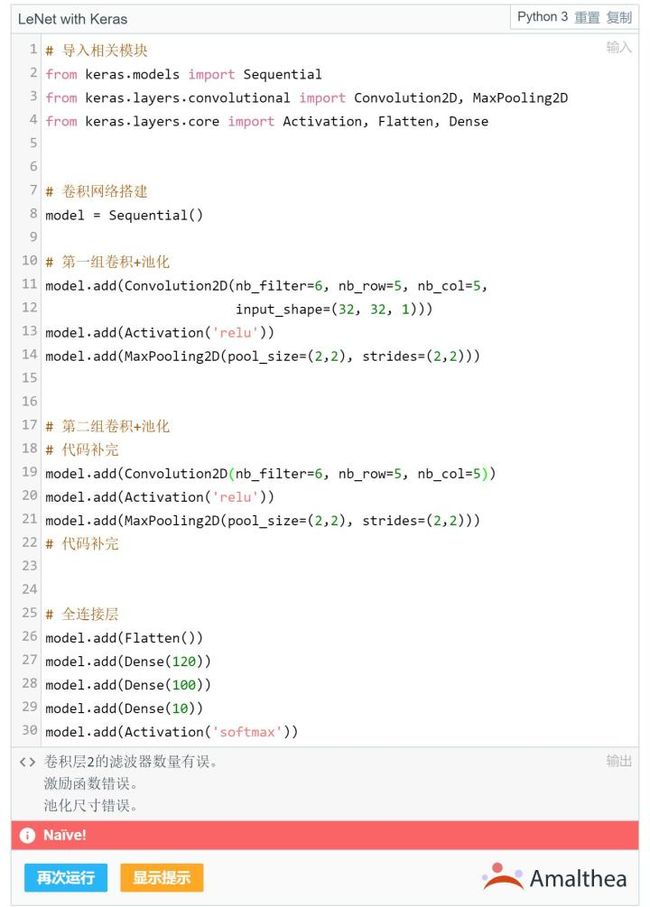
回顾LeNet的架构,补全第二组卷积+激励+池化,搭建出经典的LeNet网络。
提示:
- 第二组卷积层有16个滤波器,尺寸为8x8。
- 第二组激励层使用tanh函数
- 第二组最大池化层的尺寸和步幅均为3x3
请在下方的Python开发环境中补全代码,并点击蓝色按钮【运行】检查答案是否正确。
(需访问:卷积:如何成为一个很厉害的神经网络 - 集智专栏)
如下图,第二组卷积+激励+池化层的参数设置有误,就会得到红色提示,并指出具体的错误所在。