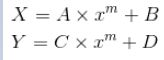设参与运算的多项式最高次数是n，那么多项式的加法，减法显然可以在O(n)时间内计算。
所以我们关心的是两个多项式的乘积。朴素的方法需要O(n^2)时间，并不够优秀。
考虑优化。
多项式乘积
方案一：分治乘法。
对于多项式X,Y，假设各有2m项，（即最高次数是2m-1)
X,Y分别可以用两个含m项的多项式来表示，即：
则
由此可见，为了计算XY，只需计算出AC, (A+B)(C+D), BD，然后用多项式加减法求得XY即可。
设含有m项的多项式相乘的时间为T(m)
则
于是容易算出时间复杂度是
，约等于
以上方法的优点在于，代码难度低，思维难度低，多项式系数任意，对运算没有任何限制。
缺点在于：太慢了！
方案二：FFT / NTT
这种方法除了快之外，没有任何优点。但仍是一种好方法。
FFT的详细推导不再描述，这里只是简单的总结。
对于多项式乘法，有一种思路，
a. 是先从系数表示法转换为点值表示法,
b. 然后乘起来（得到乘积式的点值表示法)，
c. 最后从点值表示法转变回系数表示法。
对于操作a，很容易做到O(n^2)，
对于操作b，很容易做到O(n),
对于操作c，用高斯消元可以做到O(n^3)，用拉格朗日插值法可以做到O(n^2)。
FFT则是利用了单位根的性质，将操作a和操作c优化到了O(nlogn)。
虽然在复数域中永远存在单位根，但是容易出现精度问题。
NTT并没有用复数域的单位根。
当某两个多项式相乘，系数对某一模数取模的时候，必须存在2^k次(2^k>=2n)单位根，且必须存在2的逆元。
当模数p是形如 998244353 的质数时，998244353 = 7 × 17 × 2^23 + 1，（ 2^k | phi(p) ）
设p的原根是g，则模p意义下，2^k次单位根是
。
当模数并不是满足要求的模数，我们可以知道，一次多项式乘法的结果，每一位上的数不超过n*p*p。
我们可以取多个不同的NTT模数，使得它们的乘积大于n*p*p。对每一个NTT模数做一次多项式乘法，最后用中国剩余定理计算即可。
多项式求逆
我们定义多项式A的乘法逆元B，满足A*B=1。
多项式求逆能解决多项式除法等一系列问题，因为X/Y=X*Y的逆元。
我们首先证明，多项式A存在乘法逆元的充要条件是A的常系数存在逆元。
必要性显然，因为A的常数项*B的常数项=1。
由此，我们可以求出B的常数项，接着推出一次项系数，二次项系数...
所以乘法逆元存在且唯一，充分性同样显然。
为了求逆元，一种方法是O(n^2)，即先求常数项，再推出一次项系数，继续推完整个多项式。
还有一种用O(nlogn)时间计算乘法逆元的方法，
先求出A(x)的常数项的逆元b，初始化B(x)=b，则
