01背包动态规划两种解决方案的比较
009年5月18日
15:14
01背包问题描述:一个旅行者有一个最多能用M公斤的背包,现在有N件物品,
它们的重量分别是W1,W2,...,Wn,
它们的价值分别为P1,P2,...,Pn.
若每种物品只有一件求旅行者能获得最大总价值。
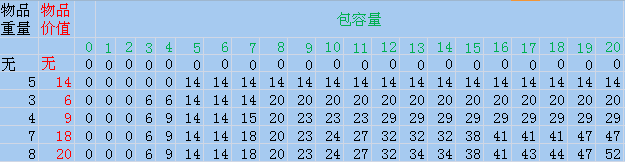
方式一:遍历M*N的数组,对应下图包的总容量M=20,物品种类数N=5
代码如下:
const int nRes=5;//5种物品
int nResWeight[nRes+1]={0,5,3,4,7,8};//每种物品对应重量
int nResValue[nRes+1]={0,14,6,9,18,20};//每种物品对应价值
const int nTotleW=20;//背包容量为20
int nValueTable[nRes+1][nTotleW+1]={0};//动态价值表,每一项对应包当前所能装入的最优值
int KitBag()
{
for(int i=1;i<=nRes;i++)
for(int j=1;j<=nTotleW;j++)//包容量逐渐递增
{
if(j>=nResWeight[i]) //当包容量大于等于当前物品重时
{//如果装入当前物品所能达最大价值>不装当前物品,包选装前面物品所能获得的最大价值
//装入当前物品所能达最大价值=当前物品价值+当前包容量j扣除当前物品重量后,剩余的容量所能装入的最大价值。
//对照上表,当遍历到i=2,j=8时,nValueTable[i-1][j-nResWeight[i]]=nValueTable[1][5]=14,满足条件就装入物品。
if(nResValue[i]+nValueTable[i-1][j-nResWeight[i]]>nValueTable[i-1][j])
nValueTable[i][j]=nResValue[i]+nValueTable[i-1][j-nResWeight[i]];//当前物品装入包.
else//当前物品不装入包,当前包容量下的最大价值仍然是原来的价值
nValueTable[i][j]=nValueTable[i-1][j];
}
else//包容量不足以装入当前物品时,沿用原来的包容量最大价值
nValueTable[i][j]=nValueTable[i-1][j];
}
cout<<"最大值为:"<
return nValueTable[nRes][nTotleW];
};
方式二:采用递归方式,遍历二叉树,并通过映射表来剪枝。
代码如下:
int RecursionBag(int nR,int nW)//传入资源数,包容量
{
if(nR==0||nW==0){
return 0;
}
if(nValueTable[nR][nW]!=0){
//当前节点是已访问过的节点,直接返回存储的最优值
return nValueTable[nR][nW];
}
if(nW>=nResWeight[nR])//包容量大于等于当前物品重
{//获得物品放入和不放入两种情况中的价值最大者
nValueTable[nR][nW]=max(nResValue[nR]+RecursionBag(nR-1,nW-nResWeight[nR]),//物品入包后的价值
RecursionBag(nR-1,nW));//物品不入包的最大价值
}
else//包容量不足以放入当前物品
nValueTable[nR][nW]=RecursionBag(nR-1,nW);
return nValueTable[nR][nW];
}
对比两种方式可知,第二种方式遍历的数据量为黄色标注结点,要小于第一种方式的数据访问量。
不过当节点深度上千后,如果包容量远小2^n,比如为 10000,这时前一种方法要快得多。估计这时,递归对访问过的节点虽然不再访问它的子节点,但是这样重复访问到的父节点数量过于庞大。