对于汉诺塔递归的实现和步骤跟踪

对于汉诺塔的理解，教材上解说的很直白，但不是很好理解，在参考了期待秋天的叶博主的“经典汉诺塔实现”之后，对汉诺塔递归思想的理解，有很大的提高。      

        设置参数：from为移动塔，depen_on为借用塔，to为目的塔；

void hanoi(int n, char from, char depend_on, char to)    //此处是汉诺塔的方法
{
    if(n==1)
        move(n,from,to);    //如果n=1时，只需要把圆盘从移动塔（from）移动到目的塔（to）上
    else
    {
        hanoi(n-1,from,to,depend_on);    //表示将n个圆盘上的n-1个圆盘从移动塔（from）移动到借用塔（depend_on）上，此时from作为移动塔传入，depend_on作为目的塔传入，to作为借用塔传入；
        move(n,from,to);    //将第n个圆盘从移动塔，移动到目的塔上
        hanoi(n-1,depend_on,from,to);    //此时，借用塔上有n-1个圆盘，变为了移动塔，目的塔依旧是目的塔，此时的移动塔变成了借用塔

    }
}

 

        这么设定参数的原因是，hanoi是递归实现的，会传过来4个参数，n表示圆盘的个数，也可以认为是圆盘的编号；
        后面三个参数抽象表示每个塔所具备的功能：
            例如：
            n=1时，传过来的A, B, C三个参数就作为from, depend_on, to三个塔，
            我们需要实现的是从A塔，移动到C塔，所以A就作为from，C就作为to，B也就是depend_on，只不过这里没用到借用塔；
            手写出来：A->C

            n=2时，
            （1）我们先是需要将n-1个圆盘从from（移动塔）移动到depen_on（借用塔）上，
            所以此时，我们要实现的是从A塔，移动到B塔，在这里，A是from，B是to了，而并非C是to。因为n-1为1，所以from到to也就是A到B；
            手写出来：A->B
            （2）当移动塔上的n-1个圆盘都移动到了借用塔上之后，剩下一个直接从移动塔移动到目的塔即可。此时的移动塔是A，目的塔是C，从from到to，即A到C；
            手写出来：A->C
            （3）最后一步就是把借用塔上的圆盘移动到目的塔上，这里需要注意：此时的借用塔的功能就是移动塔的功能，或者说，现在的借用塔就是移动塔；
            在参数传递时，将借用塔作为移动塔传入函数中，原来的目的塔依旧时目的塔，借用塔是原来的移动塔，从A到C也就是depend_on到to；
            手写为：B->C

            以此类推。

以上n=2是标准的汉诺塔递归步骤，我把n限定为2方便理解。

下面是汉诺塔的详细代码（直接可以在C编译器上实现的）：

#include

void move(int,char,char);
int i=0;   //计算需要移动的次数，作为计数器使用；
void hanoi(int n, char from, char depend_on, char to)   
{
    if(n==1)
        move(n,from,to);    //如果n=1时，只需要把圆盘从移动塔（from）移动到目的塔（to）上
    else
    {
        hanoi(n-1,from,to,depend_on);    //表示将n个圆盘上的n-1个圆盘从移动塔（from）移动到借用塔（depend_on）上，此时from作为移动塔传入，depend_on作为目的塔传入，to作为借用塔传入；
        move(n,from,to);    //将第n个圆盘从移动塔，移动到目的塔上
        hanoi(n-1,depend_on,from,to);    //此时，借用塔上有n-1个圆盘，变为了移动塔，目的塔依旧是目的塔，此时的移动塔变成了借用塔

    }
}

void move(int n, char from, char to)
{
    printf("第%d步，移动第%d个圆盘：%c->%c\n",++i,n,from,to);
}

int main(void)
{
    char a='A',b='B',c='C';    //用来表示圆盘所在的位置
    int n;    //移动圆盘的个数

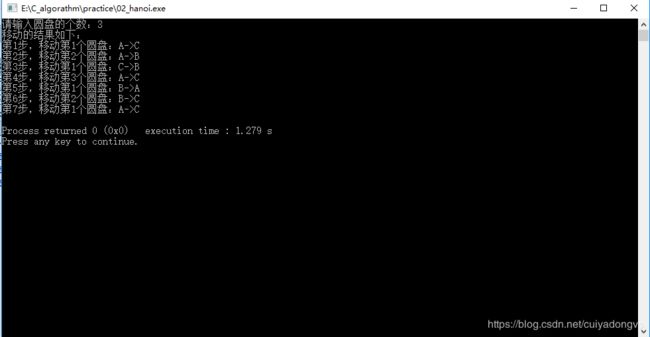
    printf("请输入圆盘的个数：");
    scanf("%d",&n);
    printf("移动的结果如下：\n");
    hanoi(n,a,b,c);

    return 0;

}