遗传算法对比模拟退火算法求解TSP问题(C++实现)
遗传算法求解TSP问题
项目源码:传送门
完成日期:2018/12/19
摘要:
利用遗传算法解决TSP问题,TSP问题的规模大小为131个城市。遗传算法的基本思想是使用模拟生物和人类进化的方法求解复杂的优化问题。利用遗传算法解决TSP问题,首先定义TSP解的个体,初始化种群,这里还做了优化,在初始的种群中加入了一些优秀的解。给种群的每一个个体用适应度函数评价,选出其中优秀的个体来进行遗传操作,遗传操作包括选择,交叉,变异。算法的终止条件是我设置的最大演化代数。算法结果能找出距离TSP最优解3%到5%误差的解,这比模拟退火解决同样规模TSP问题的解误差更加小。通过该实验得出结论,遗传算法具有较大的潜能,经过多代迭代能找到更好的解。
1.导言
要解决的问题:TSP问题,假设一个旅行商人要去n个城市,他必须经过且只经过每个城市一次,要求最后回到出发的城市,并且要求他选择的路径是所有路径中的最小值 。TSP问题是一个组合优化问题,该问题如果用穷举的方法解决,解的空间范围是指数级的。迄今为止,这类问题中没有一个找到有效算法,是NP难问题。
拟使用的方法:遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。
遗传算法涉及5大要素
- 参数编码
- 初始群体设定
- 适应度函数设计
- 遗传操作设计
- 控制参数设定
2.实验过程
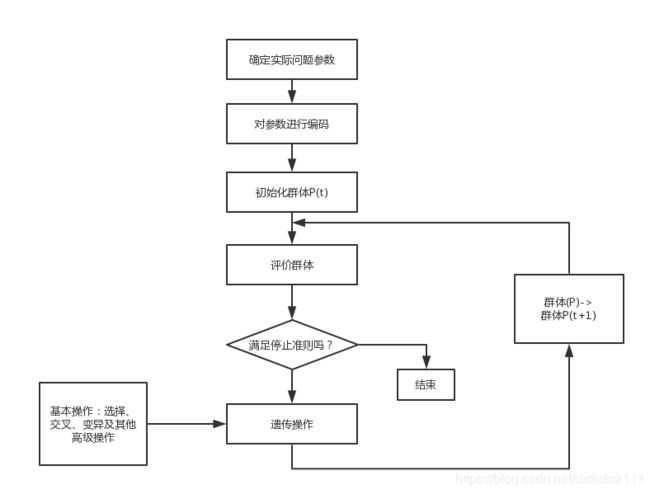
算法流程图
具体的算法思想流程:
1.基因编码
TSP问题的解是一个城市的路径,要求城市不能重复出现。所以我使用了城市大小的数组来表示一个路径的解,在遗传算法中相当于一个种群的个体。
这里用C++类Path表示一条路径,包含私有变量length记录该个体的长度,用于后面的适应值评价函数, path[nCities]用来记录路径。
// 一个个体
class Path
{
public:
// 计算路径的长度
void Calculate_length() {
length = 0;
//遍历path
for (int i = 1; i < nCities; i++) {
length += length_table[path[i - 1] - 1][path[i] - 1];
}
length += length_table[path[nCities - 1] - 1][path[0] - 1];
}
// 随机生成一个解
Path() {
length = 0;
generate_random();
Calculate_length();
}
void generate_random(){
for (int i = 0; i < nCities; ++i)
{
path[i] = i+1;
}
srand(time(0));
for (int i = 0; i < nCities; ++i)
{
int city1 = rand() % nCities;
int city2 = rand() % nCities;
int temp = path[city2];
path[city2] = path[city1];
path[city1] = temp;
}
}
double getLength(){
return length;
}
int* getPath(){
return path;
}
private:
double length;//代价,总长度
int path[nCities];//路径
};
generate_random()函数:随机生成一条合法的路径解
Calculate_length()函数,判断该路径的长度
Path()构造函数,生成一个随机解,然后初始化判断其长度
2.初始群体设定
初始群体的大小,我设置为500个个体
一开始,我的初始群体仅仅是用随机生成的个体来填充。后面我先利用了局部搜索找出一些比较好的解放入群体中,这样的操作使得种群中的基因更加好,这样更加容易找到误差小的解。
void GA::init(){
// 初始化种群
group.resize(group_size,Path());
// 给种群一些 局部搜索出来的最优解
Path new_path;
Path copy = new_path;
int j = 0;
while(j < 50000){
new_path.getNewSolution_variation();
if(copy.getLength() < new_path.getLength()){
copy = new_path;
}
j++;
}
for(int i = 0; i < 100; i++){
int num = rand()%group_size;
group[num] = copy;
}
}
3.适应度函数设计
我的适应度函数是利用一个个体的长度来设计的,这里适应值是为该个体路径长度的倒数。TSP问题中解的路径越长,解的适应性越小。所以我的适应性函数设计是正确的,当适应值越大,证明路径长度越小,所以该个体在群体更加优秀,能被选入新的群体并进行遗传操作。
double fitness[group_size];//适应性数组,用适应函数来计算
for (int i = 0; i < group_size; i++) {
fitness[i] = 1 / group[i].getLength();
}
这里的group是整个群体,fitness是适应性数组,以这个适应度函数来judge该解是否在这个群体具有优势,应不应该进行遗传操作。
4.遗传操作设计
a.选择
这里的选择是指经过了交叉,变异后的群组中选择一些优秀的个体。如何判断其优秀程度就是通过上面定义的适应性函数来进行评价。
选择方面,我采用的是轮盘赌策略,这样能让低适应值的个体也有机会去被选择,只是概率比较低。我要选择500个个体来继续进行下一代的迭代,每一次选择都会随机一个概率,让这个概率减去个体的适应值。当这个概率值低于0,这就表示轮盘落在了该个体的选择中,于是将该个体加入新种群。
void GA::choose(vector<Path> & group){
double sum_fitness = 0;
double fitness[group_size];//适应性数组,用适应函数来计算
double chance[group_size];//概率数组
double pick;//用于轮盘赌的随机数
vector<Path> next;
for (int i = 0; i < group_size; i++) {
fitness[i] = 1 / group[i].getLength();
sum_fitness += fitness[i];
}
for (int i = 0; i < group_size; i++) {
chance[i] = fitness[i] / sum_fitness;
}
//轮盘赌策略
for (int i = 0; i < group_size; i++) {
pick = ((double)rand()) / RAND_MAX;//0到1的随机数
for (int j = 0; j < group_size; j++) {
pick -= chance[j];
// 不断往下选,当pick小于0就选该个体,chance越大越有机会
if (pick <= 0) {
next.push_back(group[j]);
break;
}
//仍未选中,但是已经到最后一个了
if (j == group_size - 1) {
next.push_back(group[j]);
}
}
}
group = next;
}
b.交叉
交叉指的是选择种群中的两个个体来进行部分基因的交换,可以随机两个个体,随机个体的某一段基因。
我这里选择的是种群中临近的两个个体来进行交叉,且生成一个随机数,当该随机数小于交叉概率设定时,就将这两个个体交叉。
// 交叉
void GA::cross(vector<Path> & group) {
int point = 0;
int choice1, choice2;
while (point < group_size) {
//0到1的随机数
double pick = ((double)rand()) / RAND_MAX;
if (pick > p_cross)
//判断是否交叉
continue;
else {
// 选择临近两个点来进行交叉
// 可以改为随机选择
choice1 = point;
choice2 = point + 1;
group[choice1].getNewSolution_cross(group[choice2]);//交叉
}
point += 2;
}
}
两个个体进行交叉,要判断交叉后的结果是否合法,因为会很容易出现非法的解,如果将非法解加入种群会导致找不到TSP的正确最优解。这里我使用的是简单的单点交叉。完成交叉后要记得重新计算新解的长度,不然仍会保存旧解,导致下次遗传无法选定优秀解。
// 单点交叉,随机找一个位置
int point = rand() % (nCities - 2) + 1;
for (int i = point; i < nCities; i++) {
int temp = path[i];
path[i] = t.path[i];
t.path[i] = temp;
}
// 判断合法性
···
// 重新计算两个解的长度
Calculate_length();
t.Calculate_length();
判断解的合法性,需要对这个路径进行遍历,查找全部城市是否都存在有且只有一次。
将不合法的解变成合法解,逻辑是将上面的判断结果进行处理,如果第二次访问到这个城市,那么就等待第一个解与第二个解的重复城市,将它们进行交换。这样处理到解的最后一个城市,就能解决不合法解的情况。
// 判断与解决解的合法性
int i = 0; int j = 0;
bool count_dup_1[nCities + 1] = { false };
bool count_dup_2[nCities + 1] = { false };
while (i < nCities && j < nCities) {
// 处理冲突的城市,两解之间互相交换
if (count_dup_1[path[i]] && count_dup_2[t.path[j]]) {
int temp = path[i];
path[i] = t.path[j];
t.path[j] = temp;
i++;
j++;
}
if (i >= nCities || j >= nCities)
break;
// 统计两解的城市数量
if (!count_dup_1[path[i]]) {
count_dup_1[path[i]] = true;
i++;
}
if (!count_dup_2[t.path[j]]) {
count_dup_2[t.path[j]] = true;
j++;
}
}
c.变异
变异,又可以认为是邻域操作,我这里只是使用了之前模拟退火的操作,包括单点的交换,片段的交换,段的旋转这三种操作。
这里对每一个种群中的个体进行判断,随机一个随机数与变异概率进行比较来判断是否可以进行变异。
// 变异
void GA::variation(vector & group) {
int point = 0;
while (point < group_size) {
double pick = ((double)rand()) / RAND_MAX;
// 概率变异
if (pick < p_variation) {
group[point].getNewSolution_variation();
}
point++;
}
}
d. 更新
这个遗传操作是用来判断新形成的个体,是否可以取代父代的某些适应值低的个体,用来更新最新的种群,进行下一代的繁殖。这就是大自然当中的优胜劣汰法则。
这里的判断是根据新种群与旧种群同一下标的个体进行长度比较,当新种群个体适应值比较高的时候,用该个体代替旧种群相应个体。
// 决定子代是否能取代亲本,获取的优秀种群
void GA::judge(vector<Path> & old_group, vector<Path> & group) {
int point = 0;
while (point < group_size) {
if (old_group[point].getLength() < group[point].getLength())
group[point] = old_group[point];
point++;
}
}
这样经过历代的更替,种群会朝着适应值更高的方向进化。
5.控制参数设定
这里我对于这个131个城市的TSP问题所调整的参数有以下一些内容
const int nCities = 131; // 城市数量
const int BEST = 564; // 最优解
const int group_size = 500; // 种群大小
const int time_to_breed = 50000; // 繁殖代数
const double p_cross = 0.8; // 交叉概率
double p_variation = 0.4; // 变异概率
其中繁殖代数增加,会使遗传算法能更有潜力找到一个最优解,但是考虑运行时间与解的准确性的权衡,这里设置为50000代。
6.算法执行流程
- 选择
- 交叉
- 变异
- 替代
- 找出当代的最优解
// 繁殖多代
for (int i = 0; i < time_to_breed; i++) {
vector<Path> old_group = group;
// 选择
choose(group);
// 交叉
cross(group);
for(int j = 0; j < 5; j++){
// 变异
variation(group);
// 替代
judge(old_group,group);
}
// 找出种群中的最优解
for (int j = 0; j < group_size; j++) {
group[j].Calculate_length();
if (group[j].getLength() < best.getLength()){
best = group[j];
}
}
}
3.结果分析
实验环境: Windows10
a.算法的结果
结果图表展示:
| 次数 | 最优解 | 误差 | 运行时间 |
|---|---|---|---|
| 1 | 584.16 | 3.57% | 334.53s |
| 2 | 590.01 | 4.60% | 332.12s |
| 3 | 580.63 | 2.95% | 345.20s |
| 4 | 589.41 | 4.50% | 315.22s |
| 5 | 589.82 | 4.58% | 350.31s |
| 6 | 582.49 | 3.28% | 335.41s |
| 7 | 584.25 | 3.54% | 337.23s |
| 8 | 582.97 | 3.36% | 340.33s |
| 9 | 585.35 | 3.78% | 332.96s |
| 10 | 585.20 | 3.75% | 338.97s |
根据上述十次测试结果可以得出
最好解:
路径长度为580.63,参考最优解为564,误差为2.95%。
最差解:
路径长度为590.01,参考最优解为564,误差为4.60%。
平均值:
路径长度为585.43,参考最优解为564,误差为3.79%
标准差:
3.28107
方差:
10.76541
算法的平均速度:
运行时间为335.8s
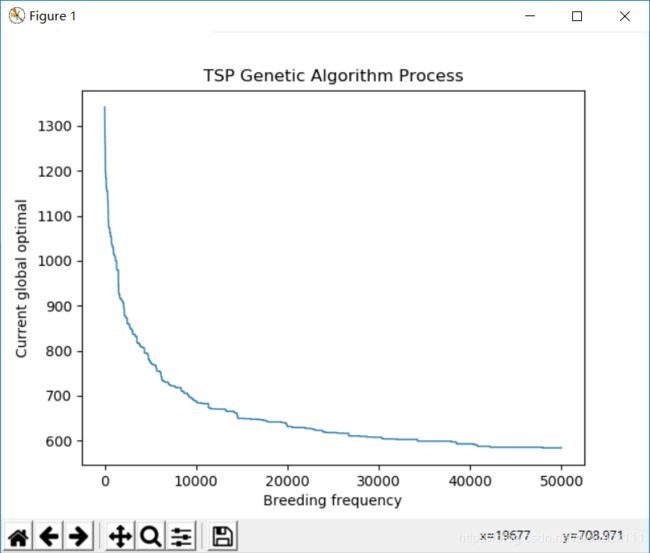
其中一次运行结果的解下降情况,横坐标是繁殖的代数,纵坐标为该代种群中的最优解
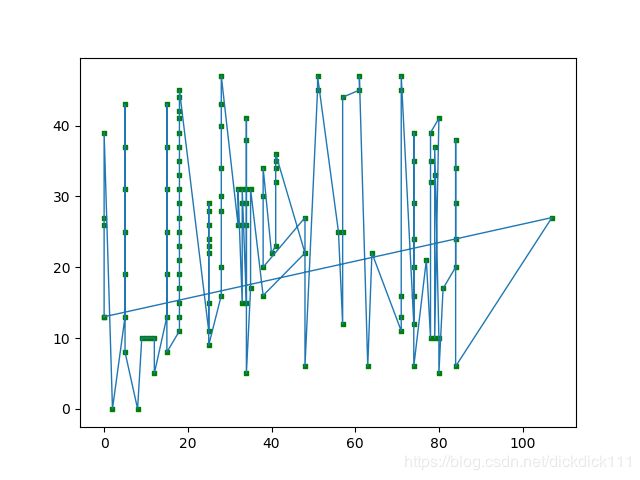
显示TSP路径的收敛情况
b.算法的性能与对比
通过遗传算法解决TSP问题得到解的精度能把误差控制在5%以内,算法的速度大概在330s左右。
与局部搜索算法对比:
- 局部搜索收敛速度较快,遗传算法收敛较慢
- 局部搜索的误差在20%左右,遗传算法可以做到3%的最小误差
- 局部搜索容易陷入局部最优,遗传算法可以跳出局部最优,查找全局最优解
与模拟退火算法对比:
- 两种算法在相近的运行时间内,模拟退火的误差维持在5%左右,稍差于遗传算法
- 模拟退火是采用单个个体进行优化,遗传算法是一种群体性算法。
- 模拟退火与遗传算法都对初解有一定的依赖性,好的初解有利于最终解
- 遗传算法可以采用并行计算来加快算法运行
c.算法的优缺点
算法能在较短的时间内,找出误差值维持在3%到5%的TSP路径,能较好的解决TSP问题。
缺点是算法在2万步左右,已经能找到误差小于10%的解,但在寻找更优解的时候,花费的时间成本确是大于之前花费找到10%的解时间。这个可以通过调整变异率来解决这一问题,当我的变异率较低的时候,我的遗传算法收敛速度很快但找到的值误差在6%以上,为了发挥其潜能,我提高了一点变异率,所以导致算法跑的速度变慢,邻域搜索更多。其次,算法 对初始种群的选择有一定的依赖性,我加入了一些局部搜索得出的优秀个体进去,提高了解的准确度
4. 结论
遗传算法的基本思想来源于达尔文的进化论,是模拟生物进化过程而设计的随机启发式全局优化方法
设计一个高效的遗传算法主要可以从以下方面入手:
- 编码
一个好的编码方式,有利于下面进行的遗传操作,在交叉,选择,变异下更加简单
- 初始化群体
可以先利用一些局部搜索或者贪心思想来求出较好的解放入种群,这样比全部个体随机生成所得到的最终解会更好
- 遗传操作
这里需要调整交叉位置、概率的参数,选择的策略,变异位置、概率的参数。这些经过几次程序的验证能找出特定数据集的较好的参数,使得该数据集能得到更好的解
- 算法的终止准则
设置遗传算法的终止条件可以由**预先设定最大演化代数;连续多代后解的适应值没有明显改进,则终止;达到明确的解目标,则终止。**我们可以根据题目的需要来改变算法的终止准则来获得满意的解,不过要在运行时间与解的准确度上做一定的权衡
比较单点搜索和多点搜索的优缺点:
- 单点搜索,以模拟退火为例子。模拟退火算法虽具有摆脱局部最优解的能力,能够以随机搜索技术从概率的意义上找出目标函数的全局最小点。但是,由于模拟退火算法对整个搜索空间的状况了解不多,不便于使搜索过程进入最有希望的搜索区域,使得模拟退火算法的运算效率不高。模拟退火算法对参数(如初始温度)的依赖性较强,且进化速度慢。
- 多点搜索,以遗传算法为例子。遗传算法具有良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱;并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度。但是遗传算法的局部搜索能力较差,导致单纯的遗传算法比较费时,在进化后期搜索效率较低。在实际应用中,遗传算法容易产生**早熟收敛的问题。**采用何种选择方法既要使优良个体得以保留,又要维持群体的多样性,一直是遗传算法中较难解决的问题。
5. 主要参考文献
- 超详细的遗传算法(Genetic Algorithm)解析
- 模拟退火算法与遗传算法性能比较
- 遗传算法的优缺点
- 基于TSP问题的物流配送路径优化的遗传算法实现 ——王吉生 华东交通大学机电工程学院
- 混合蛙跳遗传算法求解旅行商问题——唐天兵 张铭明 蒙祖强 广西大学计算机与电子信息学院