5.9模拟赛
T1:根源
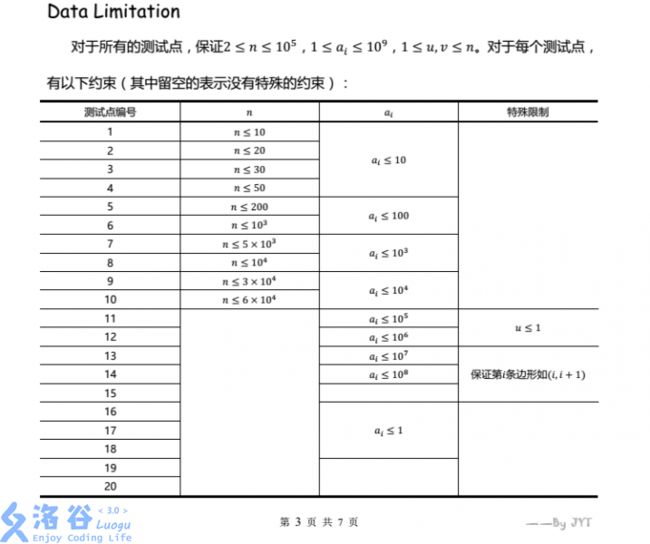
这题考场上我毫无思路,只好骗了菊花图和一条链的分;
之后经过sxd大佬的点拨,树形DP(雾
用f数组分别维护以当前节点为根的子树中选取一条链,一条路,两条路或 一条链和一条路(节点在链上)的最大权值和。
#include
#define V (to[i])
#define int long long
#define N 1000010
using namespace std;
namespace program{
int n,a[N];
int Next[N<<1],tot=0,to[N<<1],head[N<<1];
int f[N][5];
template
T read(){
T s=0;
int ch;
while(!isdigit(ch=getchar()));
do
s=s*10+ch-'0';
while(isdigit(ch=getchar()));
return s;
}
inline void add(int x,int y){
tot+=1;
Next[tot]=head[x];
to[tot]=y;
head[x]=tot;
}
inline void init(){
int x,y;
n=read();
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i();
y=read();
add(x,y);
add(y,x);
}
}
inline void dfs(int root,int fa){//当前子树根节点,父亲节点
int Max=0;
f[root][0]=a[root];
f[root][1]=a[root];
f[root][2]=a[root];
f[root][3]=0;
for(int i=head[root];i;i=Next[i]){
if(V==fa)
continue;
dfs(V,root);
f[root][2]=max(max(f[root][2],max(f[V][3]+f[root][0],f[V][0]+f[root][3])),max(f[root][1]+f[V][1],f[V][2]));
f[root][3]=max(max(f[root][3],f[V][1]+f[root][0]),max(f[V][3]+a[root],f[V][0]+a[root]+Max));
f[root][1]=max(f[root][1],max(f[V][1],f[V][0]+f[root][0]));
f[root][0]=max(f[root][0],f[V][0]+a[root]);
Max=max(Max,f[V][1]);
//0:一条链
//1:一条路
//2:两条路
//3:一条链和一条路(节点在链上)
//Max维护当前子树中不经过子树根节点的一条路的最大权值
}
}
inline void work(){
init();
dfs(1,0);
cout< T2边缘
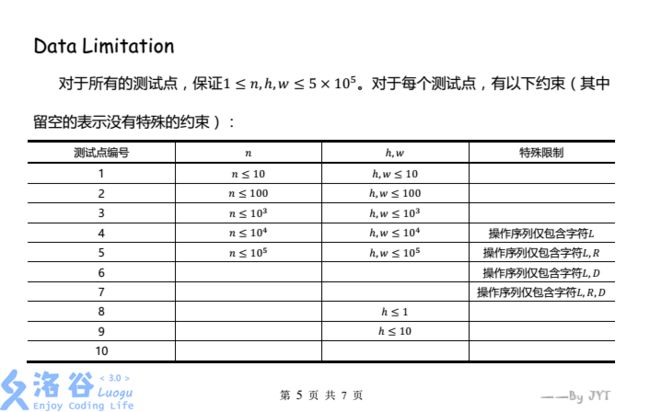
暴力h*w*n容易想到但显然TLE,就要考虑下优化当时我是这么想的:在读入n时预处理出一次操作序列中最长可以跳到哪里上下左右分别记录下来,如果跳不出去的话就+n,跳到一个操作序列可以到达的位置,这样h*w枚举,就可以过前三个点和8,9两个点了在对4,5两个点进行骗分,预计70,然而······20(似乎是在枚举时写炸了qwq
标算:在读入n时预处理一个操作序列步数之内就可以跳出的位置要跳出所需的最少步数(有点绕,建议看代码)其实和记录向上下左右最远可以跳到哪里区别不大,就多了一句判断是否小于这段距离。
上跳为U[i],下跳D[i],左跳L[i],右跳R[i]
经过这步之后,还剩下一些点无法跳出,就在可以跳出的点的基础上+n(根据递推思想(自行脑补))
只按之前思路复杂度和我是一样的,所以NB的优化来了
用A[i]数组记录min(U[i],D[i]); B[i]记录min(R[i],L[i]);
对AB进行升序排序
先做A数组:从1~h枚举对于每行找到第一个A较B更优的点,因为已排序,所以之后的一定也是A更优(同一排A的值都一样)
如图:当对第一排操作时A显然都相同,所以找到j后答案加上(w-j+1)*A[i]%Mod;
同理对B数组操作也是一样的
这样复杂度就优化为了接近O(n)的了
#include
#define Mod 1000000007
#define N 500010
using namespace std;
namespace program {
long long n,h,w,Walk[10][10];
long long D[N],U[N],R[N],L[N];
long long A[N],B[N],a[N];
long long res=0;
template
T read() {
T s=0;
long long ch;
while(!isdigit(ch=getchar()));
do
s=s*10+ch-'0';
while(isdigit(ch=getchar()));
return s;
}
inline void init() {
char ch;
n=read();
h=read();
w=read();
//D:0 U:1 R:2 L:3
//0:X 1:Y
Walk[0][0]=1;
Walk[1][0]=-1;
Walk[0][1]=0;
Walk[1][1]=0;
Walk[2][1]=1;
Walk[3][1]=-1;
Walk[2][0]=0;
Walk[3][0]=0;
for(long long i=1; i<=n; i++) {
ch=getchar();
while(ch<'A'||ch>'Z')
ch=getchar();
switch(ch) {
case 'D':
a[i]=0;
break;
case 'U':
a[i]=1;
break;
case 'R':
a[i]=2;
break;
case 'L':
a[i]=3;
break;
}
}
memset(D,20021109,sizeof D);
memset(U,20021109,sizeof U);
memset(R,20021109,sizeof R);
memset(L,20021109,sizeof L);
long long x=0,y=0;
//D:0 U:1 R:2 L:3
for(long long i=1; i<=n; i++) {
switch(a[i]){
case 0:
if(x>=0)
D[h-x]=min(D[h-x],i);
break;
case 1:
if(x<=0)
U[-x+1]=min(U[-x+1],i);
break;
case 2:
if(y>=0)
R[w-y]=min(R[w-y],i);
break;
case 3:
if(y<=0)
L[-y+1]=min(L[-y+1],i);
break;
}
x+=Walk[a[i]][0];
y+=Walk[a[i]][1];
if(x<=-h||x>=h||y<=-w||y>=w)
break;
}
if(x){
if(x<0)
for(long long i=-x+1;i<=h;i++)
U[i]=min(U[i],U[i+x]+n);
else
for(long long i=h-x;i>=1;i--)
D[i]=min(D[i],D[i+x]+n);
}
if(y){
if(y<0)
for(long long i=-y+1;i<=w;i++)
L[i]=min(L[i],L[i+y]+n);
else
for(long long i=w-y;i>=1;i--)
R[i]=min(R[i],R[i+y]+n);
}
if(x==0&&y==0){
puts("-1");
exit(0);
}
for(long long i=1;i<=h;i++)
A[i]=min(U[i],D[i]);
for(long long i=1;i<=w;i++)
B[i]=min(R[i],L[i]);
sort(A+1,A+h+1);
sort(B+1,B+w+1);
}
inline void work() {
init();
long long j=1;
for(long long i=1;i<=h;i++){
while(j<=w&&A[i]>B[j])
j+=1;
res=(res+A[i]%Mod*(w-j+1)%Mod)%Mod;
}
j=1;
for(long long i=1;i<=w;i++){
while(j<=h&&B[i]>A[j])
j+=1;
res=(res%Mod+B[i]%Mod*(h-j+1)%Mod)%Mod;
}
printf("%lld\n",res);
}
}
int main() {
program::work();
return 0;
}