拍拍贷用户及还款数据分析案例
来源:barefootgirl - kesci.com
原文链接:P2P信贷平台业务数据分析
点击以上链接 不用配置环境,直接在线运行
数据集下载链接:P2P信贷平台业务数据
这个项目来自此前拍拍魔镜数据训练营,使用了拍拍贷真实业务数据。本项目基于数据集研究了用户画像分析、资金储备、逾期还款率、借款利率、用户还款习惯、催收回款率、用户累积收益曲线的问题
1.借款人分析
首先我们来分析一下LC.csv数据集,LC (Loan Characteristics) 表为标的特征表,每支标一条记录。共有21个字段,包括一个主键(listingid)、7个标的特征和13个成交当时的借款人信息,全部为成交当时可以获得的信息。信息的维度比较广,大致可以分为基本信息,认证信息,信用信息,借款信息。
基本信息:年龄、性别;
认证信息:手机认证、户口认证、视频认证、征信认证、淘宝认证;
信用信息:初始评级、历史正常还款期数、历史逾期还款期数;
借款信息:历史成功借款金额、历史成功借款次数、借款金额、借款期限、借款成功日期
对于LC数据集我们提出以下四个问题:
1.用户画像,包含使用平台贷款业务的用户的性别比例,学历水平,是否为旧有用户,年龄分布等信息。
2.资金储备,每日借款金额大概多少?波动有多大?从而公司每日需准备多少资金可以保证不会出现资金短缺?
3.用户逾期率,借款人的初始评级、借款类型、性别、年龄等特征对于逾期还款的概率有无显著影响?哪些群体逾期还款率明显较高?
4.借款利率,哪些群体更愿意接受较高的借款利率?
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
LC = pd.read_csv('/home/kesci/input/ppdai2017/LC.csv')
LP = pd.read_csv('/home/kesci/input/ppdai2017/LP.csv')
对数据进行清洗
依次检查重复值、缺失值的处理,一致化以及异常值,数据集很干净。
#LC.info()
#LC.describe()
#观察一下年龄分布,最小17岁,最大56岁,平均年龄29岁,33岁以下的占比超过了75%。说明用户整体还是中青年。
#将年龄分为'15-20', '20-25', '25-30', '30-35', '35-40', '40+'比较合理
#观察一下借款金额分布,最小借款金额为100元,最大为50万元,平均值为4424元,低于5230的借款金额占到了75%。
#说明应该是小额借款比较多。将借款金额分为0-2000,2000-3000,3000-4000,4000-5000,5000-6000,6000以上比较合理
#LC['ListingId'].value_counts()
# LP.info()
# LP.describe()
# LP = LP.dropna(how='any')
# LP.info()
# LC = LC.dropna(how='any')
# 数据很干净
1.分析用户画像(性别、学历、年龄、是否首标)
按‘性别’、‘年龄’、‘是否首标’、‘学历认证’字段对‘借款金额’进行加总,用饼图或柱状图将结果可视化
#性别分析
male = LC[LC['性别'] == '男']
female = LC[LC['性别'] == '女']
sex = (male,female)
sex_data = (male['借款金额'].sum(), female['借款金额'].sum())
sex_idx = ('男', '女')
plt.figure(figsize=(15, 6))
plt.subplot(1,3,1)
plt.pie(sex_data, labels=sex_idx, autopct='%.1f%%')
#新老客户分析
new = LC[LC['是否首标'] == '是']
old = LC[LC['是否首标'] == '否']
newold_data = (new['借款金额'].sum(), old['借款金额'].sum())
newold_idx = ('新客户', '老客户')
plt.subplot(1,3,2)
plt.pie(newold_data, labels=newold_idx, autopct='%.1f%%')
#学历分析
ungraduate = LC[LC['学历认证'] == '未成功认证']
graduate = LC[LC['学历认证'] == '成功认证']
education_data = (ungraduate['借款金额'].sum(), graduate['借款金额'].sum())
education_idx = ('大专以下', '大专及以上')
plt.subplot(1,3,3)
plt.pie(education_data, labels=education_idx, autopct='%.1f%%')
plt.show()
#年龄分析
ageA = LC.loc[(LC['年龄'] >= 15) & (LC['年龄'] < 20)]
ageB = LC.loc[(LC['年龄'] >= 20) & (LC['年龄'] < 25)]
ageC = LC.loc[(LC['年龄'] >= 25) & (LC['年龄'] < 30)]
ageD = LC.loc[(LC['年龄'] >= 30) & (LC['年龄'] < 35)]
ageE = LC.loc[(LC['年龄'] >= 35) & (LC['年龄'] < 40)]
ageF = LC.loc[LC['年龄'] >= 40]
age = (ageA, ageB, ageC, ageD, ageE, ageF)
age_total = 0
age_percent =[]
for i in age:
tmp = i['借款金额'].sum()
age_percent.append(tmp)
age_total += tmp
age_percent /= age_total
age_idx = ['15-20', '20-25', '25-30', '30-35', '35-40', '40+']
plt.figure(figsize=(15, 8))
plt.bar(age_idx, age_percent)
for (a, b) in zip(age_idx, age_percent):
plt.text(a, b+0.001, '%.2f%%' % (b * 100), ha='center', va='bottom', fontsize=10)
plt.show()
结论:
1.男性客户的贡献的贷款金额占到了69%,可能的原因是男性更倾向于提前消费且贷款金额较大。
2.非首标的金额占比达到66%,说明用户倾向于多次使用,产品粘性较高。
3.大专以下学历的贷款金额更多,但是由于可能有很多用户并未认证学历,所以数据存在出入。
4.年龄段在25-30岁之间的借款金额最多,而20-35岁的人群占比超过75%,是该产品的主力消费人群。
2.分析资金储备
每日的借款金额大概多少?波动有多大?公司每日需要准备多少资金可以保证不会出现资金短缺?
from datetime import datetime
#分析每日贷款金额的走势
loan = LC[['借款成功日期', '借款金额']].copy()
loan['借款日期'] = pd.to_datetime(loan['借款成功日期'])
loan1 = loan.pivot_table(index='借款日期', aggfunc='sum').copy()
plt.figure(figsize=(15, 6))
plt.subplot(1,2,1)
plt.plot(loan1)
plt.xlabel('日期')
plt.ylabel('借款金额')
plt.title('每天贷款金额波动图')
#分析每月贷款金额的走势
loan['借款成功月份'] = [datetime.strftime(x, '%Y-%m') for x in loan['借款日期']]
loan2 = loan.pivot_table(index='借款成功月份', aggfunc='sum').copy()
plt.subplot(1,2,2)
plt.plot(loan2)
plt.xlabel('月份')
plt.xticks(['2015-01','2015-07','2016-01','2016-07','2017-01'])
plt.ylabel('借款金额')
plt.title('每月贷款金额波动图')
plt.show()
# 对2017年1月的数据继续进行分析,并求出平均值和标准差
loan3 = loan1.loc['2017-01']
avg = loan3['借款金额'].mean()
std = loan3['借款金额'].std()
print(avg, std)
5204663.8 2203394.1435809094
结论:
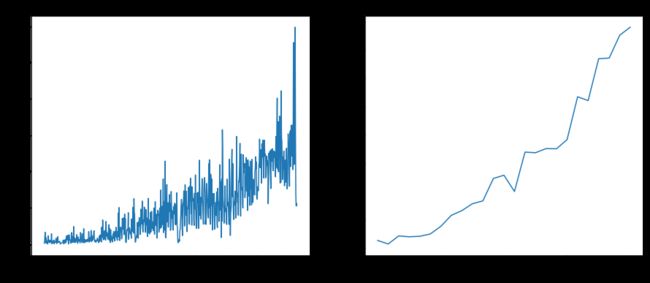
1.每日贷款金额呈现的是一个往上的趋势,但是每天的波动较大。
2.每月贷款分析结论:从2015年1月到2017年1月,月度贷款金额呈现上升趋势,上升速度随着时间增快。
3.2017年1月每日的借款金额达到5204664元,标准差为2203394,根据3σ原则,想使每日借款金额充足的概率达到99.9%,则每日公式账上需准备5204664+2203394×3=11814846元。
3.分析逾期还款率(借款人的初始评级、借款类型、性别、年龄、借款金额等特征)
逾期还款率 = 历史逾期还款期数/(历史逾期还款期数+历史正常还款期数)
#初始评级的数据划分
level_idx = ('A','B','C','D','E','F')
lev = []
for i in level_idx:
temp = LC[LC['初始评级'] == i]
lev.append(temp)
#借款类型的数据划分
kind_idx = ('电商', 'APP闪电','普通', '其他')
kind = []
for i in kind_idx:
temp = LC[LC['借款类型'] == i]
kind.append(temp)
#不同借款金额的数据划分
amount_idx = ('0-2000', '2000-3000', '3000-4000', '4000-5000', '5000-6000', '6000+')
amountA = LC.loc[(LC['借款金额'] > 0) & (LC['借款金额'] < 2000)]
amountB = LC.loc[(LC['借款金额'] >= 2000) & (LC['借款金额'] < 3000)]
amountC = LC.loc[(LC['借款金额'] >= 3000) & (LC['借款金额'] < 4000)]
amountD = LC.loc[(LC['借款金额'] >= 4000) & (LC['借款金额'] < 5000)]
amountE = LC.loc[(LC['借款金额'] >= 5000) & (LC['借款金额'] < 6000)]
amountF = LC.loc[(LC['借款金额'] >= 6000)]
amount = (amountA, amountB, amountC, amountD,amountE,amountF)
LC['逾期还款率'] = LC['历史逾期还款期数']/(LC['历史逾期还款期数']+LC['历史正常还款期数'])*100
#逾期还款率的分析图
def depayplot(i,idx,data,xlabel,title,index):
depay = []
for a in data:
tmp = a[index].mean()
depay.append(tmp)
plt.subplot(2,3,i)
plt.bar(idx, depay)
for (a, b) in zip(idx, depay):
plt.text(a, b+0.001, '%.2f%%'% b, ha='center', va='bottom', fontsize=10)
plt.xlabel(xlabel)
plt.ylabel(index)
plt.title(title)
plt.figure(figsize=(15, 10))
index = '逾期还款率'
# 根据初始评级对逾期还款率进行分析
depayplot(1,level_idx,lev,'初始评级','不同初始评级客户逾期还款率',index)
# 根据年龄对逾期还款率进行分析
depayplot(2,age_idx,age,'年龄','不同年龄客户逾期还款率',index)
# 根据借款类型对逾期还款率进行分析
depayplot(3,kind_idx,kind,'借款类型','不同借款类型客户逾期还款率',index)
# 根据性别对逾期还款率进行分析
depayplot(4,sex_idx,sex,'性别','不同性别客户逾期还款率',index)
# 根据借款金额对逾期还款率进行分析
depayplot(5,amount_idx,amount,'借款金额','不同借款金额客户逾期还款率',index)
plt.show()
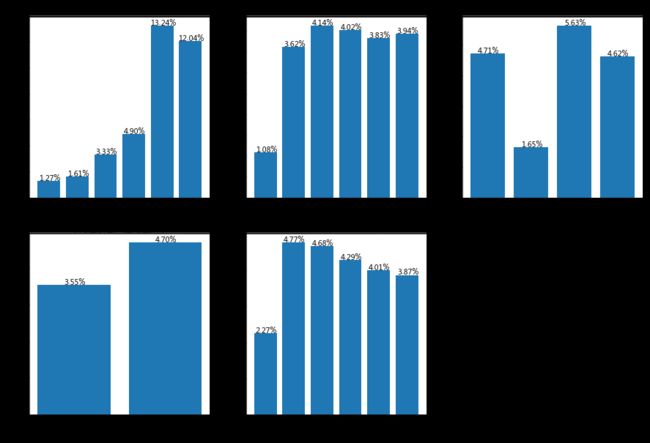
结论:
1.初始评级对于贷款者的还款能力有比较好的预测作用,EF两级反转可能是因为样本数量较少,ABCD四个等级的平均逾期还款率都比较小,而EF两级明显增大,故公司对于这两类贷款者要谨慎对待。
2.年龄对于逾期率的分布较为平均,25-30岁的年轻人可以重点关注。
3.APP闪电的逾期还款率明显低于其他三种,故公司可以多考虑与“APP闪电”借款类型的合作。
4.女性的逾期率高于男性,可能是由于生活中男性收入较女性高造成的。
5.借款金额在2000以下的逾期还款率最低,2000-3000之间的最高。可以多考虑小额贷款降低逾期风险。
4.分析借款利率(借款人的初始评级、借款类型、性别、年龄、借款金额等特征)
哪些客户群体更愿意接受较高的借款利率?
#借款利率的分析图
plt.figure(figsize=(15, 10))
index1 = '借款利率'
# 根据初始评级对借款利率进行分析
depayplot(1,level_idx,lev,'初始评级','不同初始评级客户借款利率',index1)
# 根据年龄对借款利率进行分析
depayplot(2,age_idx,age,'年龄','不同年龄客户借款利率',index1)
# 根据借款类型对借款利率进行分析
depayplot(3,kind_idx,kind,'借款类型','不同借款类型客户借款利率',index1)
# 根据性别对借款利率进行分析
depayplot(4,sex_idx,sex,'性别','不同性别客户借款利率',index1)
# 根据借款金额对借款利率进行分析
depayplot(5,amount_idx,amount,'借款金额','不同借款金额客户借款利率',index1)
plt.show()
结论:
1.年龄对于借款利率的分布较为平均,差异性很小。
2.初始评级的平均借款利率由小到大排列为ABCDFDE。
3.电商的借款利率明显低于其他三种。
4.女性所能接受的借款利率低于男性。
5.借款金额对于借款利率的分布较为平均,差异性很小。
对于以上四个问题综合分析LC数据集:
1、“男性”、“回头客”、“中青年”是拍拍贷用户群体的主要特征。
2、每日公司账上需准备7,283,728元,方可保证出现当日出借金额不足的可能性小于0.1%。
3、“初始评级”为D的群体,借款利率与E,F大致相当,但其逾期还款率却只有E,F群体的三分之一,相同的收益水平下风险大大降低,应多发展评级为D的客户或提高其贷款额度。
4、通过“app闪电”贷款的逾期还款率远低于其他项,约为其他借款类型的三分之一至四分之一,而平均借款利率却和其他项相差不大,证明“app闪电”是该公司优质的合作方,其所引流来得客户质量很高,“拍拍贷”应与“app闪电”继续加深合作。
5、“电商”中的贷款客户,收益率水平明显较低,逾期率却不低,在该群体中的贷款收益小,风险大。
6、从性别上看,男性群体贷款利率较高,逾期风险较小,相较女性一定程度上是更为优质的客户,但并不明显。
2.用户还款情况分析
基于LCLP.csv 数据,分析用户的还款习惯(提前一次性全部还款 、部分提前还款以及逾期还款)的金额占比。
将数据集按借款金额分组,并按还款状态和还款日期分成四种还款情况并进行统计:
(1)一次性全部还款:其还款状态标记为‘已提前还清该标全部欠款’;
(2)部分提前还款:其还款状态标记为’已正常还款’,并且当期的还款日期早于到期日期;
(3)正常还款:其还款状态标记为’已正常还款’,并且当期的还款日期即为到期日期;
(4)逾期还款:还款状态标记为‘未还款’,‘已逾期还款’或者‘已部分还款’。
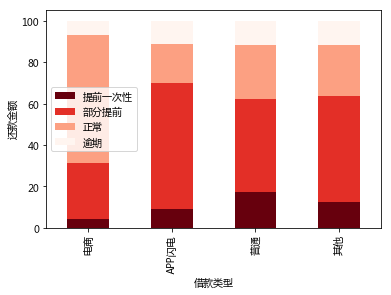
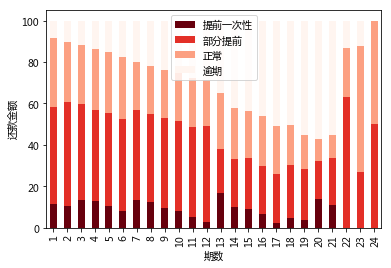
用百分堆积柱状图展示在不同年龄段(15 -20 ,20 -25 ,25 -30 , 30-35 ,35 -40 ,40+ ),不同性别( 男、女),不同初始评级(A-F),不同借款类型、不同借款金额(1-1000,1000 -2000,2000-3000,3000+)、不同期数(1-24)的走势。
# 删除尚未到期的记录
LP = LP[LP['到期日期'] <= LP['recorddate']]
#LP.info()
#LP.describe()
# 将LC和LP两个表融合起来
LCLP = pd.merge(LC, LP, how='left', on=['ListingId'])
# 删除数据不全的记录
LCLP = LCLP.dropna(how='any')
# LCLP.info()
#LCLP.describe()
#定义用户还款习惯分析可视化函数
def repayhabit(group,num,idx,xlabel,color):
# 一次性全部还款
onetime = []
for a in group:
ot = a.loc[a['还款状态'] == 3]['应还本金'].sum(
) + a.loc[a['还款状态'] == 3]['应还利息'].sum()
onetime.append(ot)
# 部分提前还款
partial = []
for a in group:
pa = a.loc[(a['还款状态'] == 1) & (a['还款日期'] < a['到期日期'])]['应还本金'].sum(
) + a.loc[(a['还款状态'] == 1) & (a['还款日期'] < a['到期日期'])]['应还利息'].sum()
partial.append(pa)
# 逾期还款
pastdue = []
for a in group:
pas = a.loc[(a['还款状态'] == 2) | (a['还款状态'] == 4)|(a['还款状态'] == 0)]['应还本金'].sum() + \
a.loc[(a['还款状态'] == 2) | (a['还款状态'] == 4)|(a['还款状态'] == 0)]['应还利息'].sum()
pastdue.append(pas)
# 正常还款
normal = []
for a in group:
nm = a.loc[(a['还款状态'] == 1) & (a['还款日期'] == a['到期日期'])]['应还本金'].sum(
) + a.loc[(a['还款状态'] == 1) & (a['还款日期'] == a['到期日期'])]['应还利息'].sum()
normal.append(nm)
tot = []
for i in range(num):
t = onetime[i]+partial[i]+pastdue[i]+normal[i]
tot.append(t)
print(tot)
temp = []
for i in range(num):
tp = (100 * onetime[i] / tot[i], 100 * partial[i] / tot[i],
100 * normal[i] / tot[i], 100 * pastdue[i] / tot[i])
temp.append(tp)
df = pd.DataFrame(temp)
df.index = idx
df.columns = ('提前一次性', '部分提前', '正常', '逾期')
print(df)
df.plot(kind='bar', colormap=color, stacked=True)
plt.ylabel('还款金额')
plt.xlabel(xlabel)
plt.legend(loc='best')
plt.show()
# 分析不同借款金额用户的还款情况
amountA = LCLP.loc[(LCLP['借款金额'] > 0) & (LCLP['借款金额'] < 2000)]
amountB = LCLP.loc[(LCLP['借款金额'] >= 2000) & (LCLP['借款金额'] < 3000)]
amountC = LCLP.loc[(LCLP['借款金额'] >= 3000) & (LCLP['借款金额'] < 4000)]
amountD = LCLP.loc[(LCLP['借款金额'] >= 4000) & (LCLP['借款金额'] < 5000)]
amountE = LCLP.loc[(LCLP['借款金额'] >= 5000) & (LCLP['借款金额'] < 6000)]
amountF = LCLP.loc[(LCLP['借款金额'] >= 6000)]
amountgroup = [amountA, amountB, amountC, amountD,amountE,amountF]
repayhabit(amountgroup,6,amount_idx,'借款金额','Greys_r')
[28456834.85, 69903191.44000001, 99595369.9, 72161874.03, 51083566.29000001, 269236628.2506]
提前一次性 部分提前 正常 逾期
0-2000 10.204426 60.954742 16.233811 12.607020
2000-3000 10.208217 54.959603 20.400835 14.431346
3000-4000 14.874141 50.961604 21.902815 12.261440
4000-5000 14.678874 50.698304 22.775784 11.847038
5000-6000 15.703463 50.299053 23.239861 10.757622
6000+ 11.688029 39.376116 39.790049 9.145806
在根据借款金额分组中,得到结果如下:
A组(0-2000):总金额2.85千万。(1)一次性全部还款:占比 10.20%;(2)部分提前还款:占比60.95%;(3)正常还款:占比 16.23%; (4)逾期还款:占比 12.61%。
B组(2000-3000):总金额 7千万。(1)一次性全部还款:占比 10.21%;(2)部分提前还款:占比54.96%;(3)正常还款:占比 20.40%; (4)逾期还款:占比 14.43%。
C组(3000-4000):总金额 10千万。(1)一次性全部还款:占比 14.87%;(2)部分提前还款:占比50.96%;(3)正常还款:占比 21.90%; (4)逾期还款:占比 12.26%。
D组(4000-5000):总金额 7.22千万。(1)一次性全部还:占比 14.68%;(2)部分提前还款:占比50.70%;(3)正常还款:占比 22.78%; (4)逾期还款:占比 11.85%。
E组(5000-6000):总金额 5.11千万。(1)一次性全部还款:占比 15.70%;(2)部分提前还款:占比50.30%;(3)正常还款:占比 23.24%; (4)逾期还款:占比 10.76%。
F组(6000+):总金额 26.92千万。(1)一次性全部还款:占比 11.69%;(2)部分提前还款:占比39.38%;(3)正常还款:占比 39.79%; (4)逾期还款:占比 9.15%。
从对借款金额分组的统计结果以及上图结果中可以看出:
(1)借款总额6000元以上最多,3000-4000其次,说明3000-4000元的借款金额是最多的。
(2)逾期风险在各金额组表现比较平均,其中2000-3000最大,6000+最小。
(3)随着标的金额增加,部分提前还款的总金额比例在减少,正常还款的总金额比例在增加。
# 分析不同年龄段用户的还款情况
ageA = LCLP.loc[(LCLP['年龄'] >= 15) & (LCLP['年龄'] < 20)]
ageB = LCLP.loc[(LCLP['年龄'] >= 20) & (LCLP['年龄'] < 25)]
ageC = LCLP.loc[(LCLP['年龄'] >= 25) & (LCLP['年龄'] < 30)]
ageD = LCLP.loc[(LCLP['年龄'] >= 30) & (LCLP['年龄'] < 35)]
ageE = LCLP.loc[(LCLP['年龄'] >= 35) & (LCLP['年龄'] < 40)]
ageF = LCLP.loc[LCLP['年龄'] >= 40]
agegroup = [ageA, ageB, ageC, ageD, ageE, ageF]
repayhabit(agegroup,6,age_idx,'年龄','Reds_r')
[1325708.5400000003, 85978811.91999999, 203407279.9106, 149443150.8962, 79947743.0043, 70334770.4895]
提前一次性 部分提前 正常 逾期
15-20 10.441107 62.896452 13.114767 13.547674
20-25 13.428313 53.199581 20.048697 13.323409
25-30 14.002901 47.665900 26.687108 11.644091
30-35 12.363756 43.932650 33.824134 9.879460
35-40 10.805522 44.388718 34.672769 10.132990
40+ 10.882495 42.854777 37.205296 9.057432
在年龄分组中,得到结果如下:
A组(15-20岁):总金额0.13千万。(1)一次性全部还款:占比 10.44%;(2)部分提前还款:占比62.90%;(3)正常还款:占比 13.11%; (4)逾期还款:占比 13.55%。
B组(20-25岁):总金额 8.60千万。(1)一次性全部还款:占比 13.43%;(2)部分提前还款:占比53.2%;(3)正常还款:占比 20.05%; (4)逾期还款:占比 13.32%。
C组(25-30岁):总金额 20.34千万。(1)一次性全部还款:占比 14.00%;(2)部分提前还款:占比47.67%;(3)正常还款:占比 26.69%; (4)逾期还款:占比 11.64%。
D组(30-35岁):总金额 14.94千万。(1)一次性全部还款:占比 12.36%;(2)部分提前还款:占比43.92%;(3)正常还款:占比 33.82%; (4)逾期还款:占比 9.88%。
E组(35-40岁):总金额 8.00千万。(1)一次性全部还款:占比 10.81%;(2)部分提前还款:占比44.39%;(3)正常还款:占比 34.67%; (4)逾期还款:占比 10.13%。
F组(40岁+):总金额 7.03千万。(1)一次性全部还款:占比 10.88%;(2)部分提前还款:占比42.85%;(3)正常还款:占比 37.21%; (4)逾期还款:占比 9.06%。
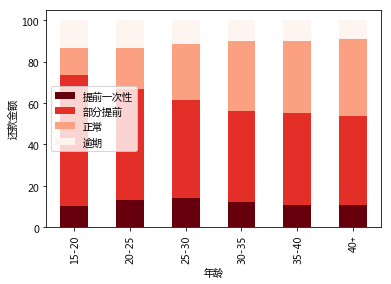
从对年龄分组的统计结果以及上图结果中可以看出:
(1)拍拍贷的客户群体中25-30岁年龄组的贷款金额最高,15-20岁最低;
(2)各年龄组的还款习惯大体一致,从金额上来说,部分提前还款和正常还款是最常用的方式;
(3)逾期还款风险最高的年龄组为15-20岁组;
(4)25-30岁年龄组一次性提前还款的金额占比最高。
# 分析不同性别用户的还款情况
male = LCLP.loc[LCLP['性别'] == "男"]
female = LCLP.loc[LCLP['性别'] == "女"]
sexgroup = (male,female)
repayhabit(sexgroup,2,sex_idx,'性别','Greens_r')
[431899402.1953, 158538062.5653]
提前一次性 部分提前 正常 逾期
男 13.159444 45.775236 30.093425 10.971895
女 11.417458 48.638828 29.114713 10.829001
在男女性别组中,得到结果如下:
男性:总还款金额 43.19千万。(1)一次性全部还款占比 13.16%;(2)部分提前还款占比45.78%;(3)正常还款占比 30.09%; (4)逾期还款占比10.97%。
女性:总还款金额 15.85千万。(1)一次性全部还款占比 11.42%;(2)部分提前还款占比48.64%;(3)正常还款占比29.11%; (4)逾期还款占比10.83%。
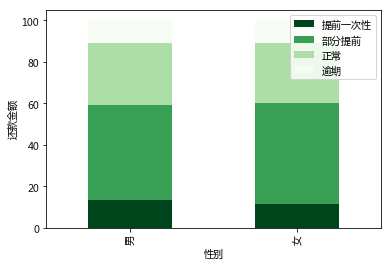
从对男女性别组的统计结果以及上图结果中可以看出:
(1)拍拍贷男性客户的贷款金额约为女性客户的2.7倍;
(2)男性及女性的还款习惯大体上比较一致,从金额上来说,部分提前还款>正常还款>一次性提前还款>逾期还款;
(3)男性客户一次性提前还款的金额占比较女性为高;
(4)女性逾期还款的风险略低于男性;
(5)女性部分提前还款的金额占比略大于男性。
# 分析不同初始评级客户的还款情况
levelgroup = []
for i in level_idx:
l = LCLP[(LCLP['初始评级'] == i)]
levelgroup.append(l)
repayhabit(levelgroup,6,level_idx,'初始评级','Blues_r')
[24260113.047399998, 129789781.91, 292672443.2151, 131419854.39039999, 10771732.247699998, 1523539.95]
提前一次性 部分提前 正常 逾期
A 10.951641 42.540019 39.727788 6.780552
B 7.686131 37.447042 47.651688 7.215139
C 14.192953 49.919494 24.995052 10.892502
D 14.592841 49.269359 21.846049 14.291750
E 13.213394 40.965391 22.906776 22.914440
F 10.752586 41.241621 20.679682 27.326111
在初始评级分组中,得到结果如下:
A级:总金额2.43千万。(1)一次性全部还款:占比 10.95%;(2)部分提前还款:占比42.54%;(3)正常还款:占比 39.73%; (4)逾期还款:占比 6.78%。
B级:总金额 12.98千万。(1)一次性全部还款:占比 7.68%;(2)部分提前还款:占比37.45%;(3)正常还款:占比 47.65%; (4)逾期还款:占比 7.22%。
C级:总金额 29.27千万。(1)一次性全部还款:占比 14.19%;(2)部分提前还款:占比49.92%;(3)正常还款:占比 25.00%; (4)逾期还款:占比 10.89%。
D级:总金额 13.14千万。(1)一次性全部还款:占比 14.59%;(2)部分提前还款:占比49.27%;(3)正常还款:占比 21.85%; (4)逾期还款:占比 14.29%。
E级:总金额 1.08千万。(1)一次性全部还款:占比 13.21%;(2)部分提前还款:占比40.97%;(3)正常还款:占比 22.91%; (4)逾期还款:占比 22.91%。
F级:总金额 0.15千万。(1)一次性全部还款:占比 10.75%;(2)部分提前还款:占比41.24%;(3)正常还款:占比 20.68%; (4)逾期还款:占比 27.33%。
从对初始评级分组的统计结果可以看出:
(1)B级客户借款总额最多,占到了大约50%的金额。B、C、D级客户是借款的主力军。
(2)提前一次性还款的占比相对比较平均,其中D级最大为14.59%。
(3)逾期风险随着级别而呈总体增加趋势,F级客户的逾期占比达到了27.33%。
(4)部分提前和正常还款还是占到了大多数。
(5)总的来说,初始评级具有重要的参考意义。
# 分析不同借款类型客户的还款情况
kindgroup = []
for i in kind_idx:
l = LCLP[(LCLP['借款类型'] == i)]
kindgroup.append(l)
repayhabit(kindgroup,4,kind_idx,'借款类型','Reds_r')
[85700890.47, 74452365.96, 234675993.36, 195608214.9706]
提前一次性 部分提前 正常 逾期
电商 4.218635 26.927505 62.071671 6.782188
APP闪电 8.959958 61.125398 18.677700 11.236944
普通 17.162002 45.092948 26.095824 11.649226
其他 12.461221 51.329790 24.430785 11.778204
在借款类型分组中,得到结果如下:
电商:总金额8.57千万。(1)一次性全部还款:占比 4.22%;(2)部分提前还款:占比26.93%;(3)正常还款:占比 62.07%; (4)逾期还款:占比 6.78%。
APP闪电:总金额 7.45千万。(1)一次性全部还款:占比 8.96%;(2)部分提前还款:占比61.13%;(3)正常还款:占比 18.68%; (4)逾期还款:占比11.24%。
普通:总金额 23.47千万。(1)一次性全部还款:占比 17.16%;(2)部分提前还款:占比45.09%;(3)正常还款:占比 26.10%; (4)逾期还款:占比 11.65%。
其他:总金额 19.56千万。(1)一次性全部还款:占比 12.46%;(2)部分提前还款:占比51.33%;(3)正常还款:占比 24.43%; (4)逾期还款:占比 11.78%。
从对借款类型分组的统计结果可以看出:
(1)普通借款类型的借款金额总数最大,其次是其他,电商和APP闪电差不多。
(2)逾期风险电商最低,为6.78%。其他三种类型差不多。
(3)部分提前和正常还款还是占到了大多数。值得注意的是除了电商,其他三种类型的部分提前还款都占比很大。
term_idx = ('1','2','3','4','5','6','7','8','9','10','11','12','13','14','15','16','17','18','19','20','21','22','23','24')
termgroup = []
for i in range(1,25):
term = LCLP.loc[(LCLP['期数'] == i)]
termgroup.append(term)
repayhabit(termgroup,24,term_idx,'期数','Reds_r')
[201565330.19059998, 160494654.9011, 142197065.14570004, 119076424.03460002, 98747185.4339, 80930357.9448, 40878559.982200004, 33897402.88249999, 27118560.888, 21440574.8308, 16173580.82, 11798205.459999999, 829538.13, 712179.6699999999, 634899.49, 544136.9299999999, 450818.11, 376328.06, 170209.27, 127468.83, 64092.6, 16738.09, 6095.860000000001, 1636.3400000000001]
提前一次性 部分提前 正常 逾期
1 11.323967 46.902638 33.431895 8.341499
2 10.627492 50.312785 28.719538 10.340185
3 13.429248 46.155704 28.693458 11.721591
4 12.671416 44.157855 29.482901 13.687827
5 10.720721 44.604374 29.438926 15.235980
6 8.034741 44.478341 29.986734 17.500184
7 13.244753 43.730144 22.927067 20.098036
8 12.189846 42.894606 23.201825 21.713723
9 9.581578 43.431477 23.247505 23.739439
10 7.876236 43.417232 23.379967 25.326566
11 5.279194 43.232885 23.974747 27.513173
12 2.922282 46.334268 21.896949 28.846501
13 16.774186 21.147695 27.364840 34.713280
14 9.758560 23.252014 24.693067 42.296359
15 8.801518 24.895919 22.573134 43.729430
16 6.470489 23.249683 24.300979 45.978849
17 2.506725 23.486991 23.340262 50.666021
18 4.905321 25.221409 19.448053 50.425217
19 3.610555 24.795682 16.487475 55.106288
20 13.697341 18.319506 10.687672 57.295482
21 11.058032 22.625342 11.033629 55.282997
22 0.000000 63.308418 23.442997 13.248585
23 0.000000 26.843464 60.871805 12.284731
24 0.000000 50.000000 50.000000 0.000000
从对期数分组的统计结果可以看出:
(1)借款金额是随着期数增加呈现出下降的趋势。
(2)不同的还款行为在不同的借款期限下的表现差异比较大,部分提前还款和正常还款是最常用的方式;
(3)逾期风险随着借款期限变长而呈总体增加趋势,期限为20个月的逾期金额占比为最高,达到了57.30%;
(4)期限为13个月的提前一次性还款占比最高,达到了16.77%。
(5)借款期限太长的样本数量太少,不能排除偶然性。
3.计算金额催收回款率(催收回本金/所有逾期本金)
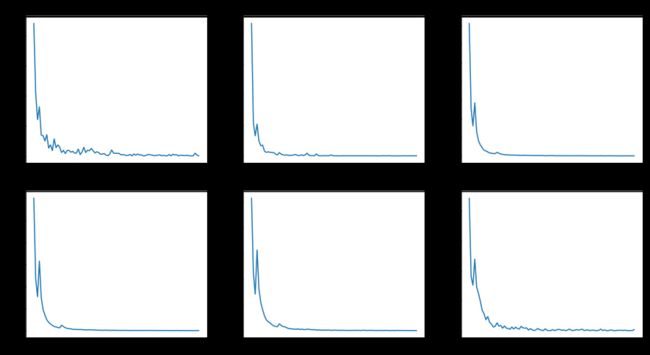
在不同等级(A-F)、不同借款期数(1-24)和不同借款金额(0-2000,2000-3000,3000-4000,4000-5000,5000-6000,6000+)等,随逾期天数增加而呈现的走势。
1)x轴为逾期天数,y轴为金额催收回款率,不同参数对应不同曲线;
2)催收回款的定义为逾期90天之内的逾期还款。
from datetime import datetime,timedelta
#LCLP.info()
LCLP['recorddate'] = pd.to_datetime(LCLP['recorddate'])
LCLP['到期日期'] = pd.to_datetime(LCLP['到期日期'])
LCLP['还款日期'] = pd.to_datetime(LCLP['还款日期'], errors='coerce')
LCLP['lateday'] = LCLP['还款日期']-LCLP['到期日期']
depay = LCLP[LCLP['lateday']>timedelta(days=0)]
#不同等级(A-F)随逾期天数催收还款率的走势
df = depay.groupby(['初始评级','lateday'])['应还本金'].sum()
df1 = df.to_frame().pivot_table(index='lateday',columns = '初始评级', values ='应还本金')
tmp = df1.fillna(0)
df2 = depay.groupby(['初始评级'])['应还本金'].sum()
tmp_1 = tmp[tmp.index <= timedelta(days=90)]
tmp_1 = tmp_1/df2
plt.figure(figsize=(15, 8))
for i in range(6):
plt.subplot(2,3,i+1)
plt.plot(range(90),tmp_1[level_idx[i]])
plt.title(level_idx[i])
plt.show()
不同等级(A-F)随逾期天数催收还款率的走势大致相同,也就是大部分人都在逾期十天之内还款,说明他们有可能忘记还款;特别是在4、5天的还款的人数和金额最多。
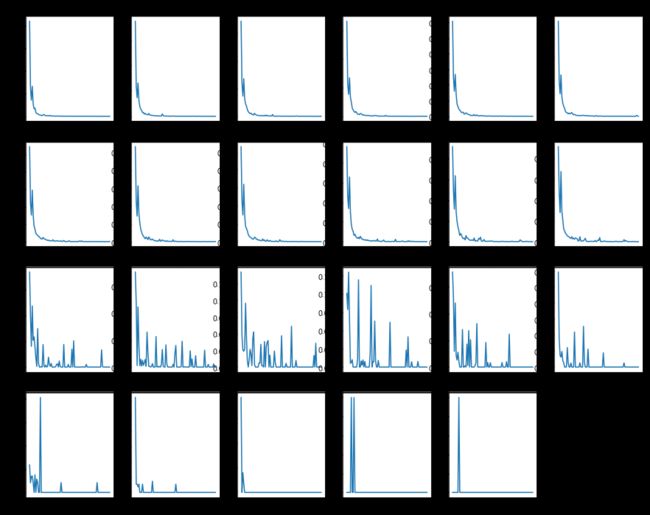
#不同借款期数(1-24)随逾期天数催收还款率的走势
#由于期数为24的项目不存在逾期还款的现象,所以只对1-23进行分析
df = depay.groupby(['期数','lateday'])['应还本金'].sum()
df1 = df.to_frame().pivot_table(index='lateday',columns = '期数', values ='应还本金')
tmp = df1.fillna(0)
df2 = depay.groupby(['期数'])['应还本金'].sum()
tmp_1 = tmp[tmp.index <= timedelta(days=90)]
tmp_1 = tmp_1/df2
plt.figure(figsize=(15, 12))
for i in range(1,24):
plt.subplot(4,6,i)
plt.plot(range(90),tmp_1[i])
plt.xticks([0,30,60,90])
plt.title(str(i))
plt.show()
不同借款期数(1-24)的金额收回款率随逾期天数的趋势没有明显的规律。在12期及之前大部分人都在逾期十天之内还款,特别是在4、5天的还款的人数和金额最多。 但是13之后呈现出10天之后回款率的依然很大。也有可能是因为数据量导致异常值凸显,但是也说明了借款期数长的回款率不够稳定。
#不同借款金额随逾期天数催收还款率的走势
def function(a):
if a>0 and a<2000:
return '0-2000'
elif a>=2000 and a<3000:
return '2000-3000'
elif a>=3000 and a<4000:
return '3000-4000'
elif a>=4000 and a<5000:
return '4000-5000'
elif a>=5000 and a<6000:
return '5000-6000'
else:
return '6000+'
depay['金额类型'] = depay.apply(lambda x:function(x['借款金额']),axis=1)
df = depay.groupby(['金额类型','lateday'])['应还本金'].sum().copy()
df1 = df.to_frame().pivot_table(index='lateday',columns = '金额类型', values ='应还本金')
tmp = df1.fillna(0)
df2 = depay.groupby(['金额类型'])['应还本金'].sum()
tmp_1 = tmp[tmp.index <= timedelta(days=90)]
tmp_1 = tmp_1/df2
plt.figure(figsize=(15, 8))
for i in range(6):
plt.subplot(2,3,i+1)
plt.plot(range(90),tmp_1[amount_idx[i]])
plt.xticks([0,30,60,90])
plt.title(amount_idx[i])
plt.show()
对不同借款金额对于进入催收回款率影响较大,借款金额越多,逾期的可能性就越大。
4.累积收益曲线
LCIS数据提供了该客户投资的从2015年1月1日起成交的所有标。包括投标记录和还款状况。请计算并画出该投资人从2016年9月开始到2017年2月,每月月底的累计收益曲线。
from datetime import datetime,timedelta
LCIS = pd.read_csv("/home/kesci/input/ppdai2017/LCIS.csv",encoding = 'utf-8')
# 计算从2016年9月至2017年2月所有的利息
def getinterest(df):
df_1 = df[['ListingId','标当前状态','上次还款日期','上次还款利息']]
df_1 = df_1[(df_1['标当前状态'] =='正常还款中') | (df_1['标当前状态'] =='已还清')]
df_1['上次还款日期'] = df_1['上次还款日期'].where(df_1['上次还款日期'].notnull(),'2016/08/31')
df_1['上次还款日期'] = pd.to_datetime(df_1['上次还款日期'], errors='coerce')
df_1 = df_1[df_1['上次还款日期']>='2016-09-01'].drop_duplicates()
df_1_1 = df_1.groupby(['上次还款日期'])['上次还款利息'].sum().to_frame().reset_index()
return df_1_1
# 计算从2016年9月至2017年2月所有的亏损
def getloss(df):
df_2 = df[['ListingId', '待还本金', '标当前状态', '上次还款日期', '下次计划还款日期', 'recorddate']]
df_2 = df_2[(df_2['标当前状态']=='逾期中')]
df_2['下次计划还款日期'] = pd.to_datetime(df_2['下次计划还款日期'], errors='coerce')
df_2['recorddate'] = pd.to_datetime(df_2['recorddate'], errors='coerce')
# 往回看90天到2016-06-03
df_2 = df_2[df_2['下次计划还款日期']>='2016-06-03']
df_2['delay'] = df_2.apply(lambda x: (x['recorddate'] - x['下次计划还款日期']).days, axis = 1)
df_2_1 = df_2[df_2['delay']>=90].sort_values(['ListingId','delay'])
df_2_1['date'] = df_2['下次计划还款日期'] + timedelta(days=90)
df_2_2 = df_2_1.loc[df_2_1.sort_values('recorddate').iloc[:,0].drop_duplicates().index]
df_2_2 = df_2_2[['date','待还本金']].groupby(['date'])['待还本金'].sum().to_frame().reset_index()
return df_2_2
# merge gain and loss
def profit(df):
df_1_1 = getinterest(df)
df_2_2 = getloss(df)
df_now = pd.merge(df_1_1,df_2_2, how = 'left', left_on = '上次还款日期', right_on = 'date')
df_now['待还本金'] = df_now['待还本金'].where(df_now['待还本金'].notnull(),0)
df_now['差别'] = df_now['上次还款利息'] - df_now['待还本金']
return df_now
def draw(df):
df_now = profit(df)
plt.plot(df_now['上次还款日期'], np.cumsum(df_now['差别']), label="利息")
plt.title('累积收益曲线')
plt.xlabel('时间')
plt.ylabel('收益金额')
plt.show()
draw(LCIS)
调用draw()函数,可以对任一用户的数据画出累积收益曲线。