41. 当不知道数据所带标签时，可以使用哪种技术促使带同类标签的数据与带其他标签的数据相分离？(B)
A. 分类 B. 聚类 C. 关联分析 D. 隐马尔可夫链
42. 建立一个模型，通过这个模型根据已知的变量值来预测其他某个变量值属于数据挖掘的哪一类任务？(C)
A. 根据内容检索 B. 建模描述 C. 预测建模 D. 寻找模式和规则
43. 以下哪种方法不属于特征选择的标准方法？(D)
A嵌入 B 过滤 C 包装 D 抽样
44. 请用python编写函数find_string，从文本中搜索并打印内容，要求支持通配符星号和问号。例子：
>>>find_string('hello\nworld\n','wor')
['wor']
>>>find_string('hello\nworld\n','l*d')
['ld']
>>>find_string('hello\nworld\n','o.')['or']
答案
def find_string(str,pat):
import re
return re.findall(pat,str,re.I)
45. 说下红黑树的五个性质红黑树，一种二叉查找树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。
红黑树，作为一棵二叉查找树，满足二叉查找树的一般性质。下面，来了解下 二叉查找树的一般性质。
二叉查找树，也称有序二叉树（ordered binary tree），或已排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：
若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
任意节点的左、右子树也分别为二叉查找树。
没有键值相等的节点（no duplicate nodes）。
因为一棵由n个结点随机构造的二叉查找树的高度为lgn，所以顺理成章，二叉查找树的一般操作的执行时间为O(lgn)。但二叉查找树若退化成了一棵具有n个结点的线性链后，则这些操作最坏情况运行时间为O(n)。
红黑树虽然本质上是一棵二叉查找树，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
但它是如何保证一棵n个结点的红黑树的高度始终保持在logn的呢？这就引出了红黑树的5个性质：
每个结点要么是红的要么是黑的。 根结点是黑的。
每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的。
如果一个结点是红的，那么它的两个儿子都是黑的。
对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。 正是红黑树的这5条性质，使一棵n个结点的红黑树始终保持了logn的高度，从而也就解释了上面所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)”这一结论成立的原因。
更多请参见此文： 《教你初步了解红黑树》
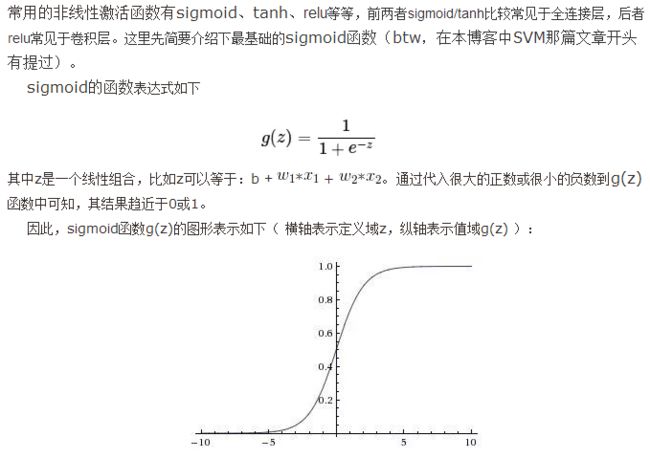
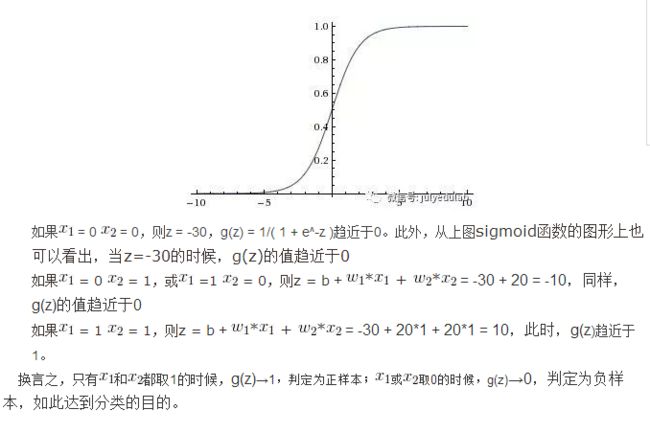
46. 简单说下sigmoid激活函数
47. 什么是卷积?
对图像（不同的数据窗口数据）和滤波矩阵（一组固定的权重：因为每个神经元的多个权重固定，所以又可以看做一个恒定的滤波器filter）做 内积（逐个元素相乘再求和）的操作就是所谓的『卷积』操作，也是卷积神经网络的名字来源。
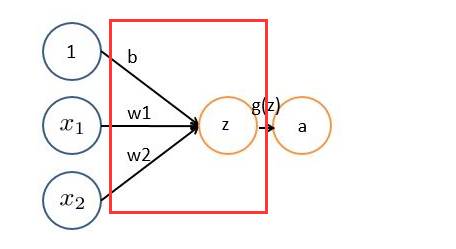
非严格意义上来讲，下图中红框框起来的部分便可以理解为一个滤波器，即带着一组固定权重的神经元。多个滤波器叠加便成了卷积层。
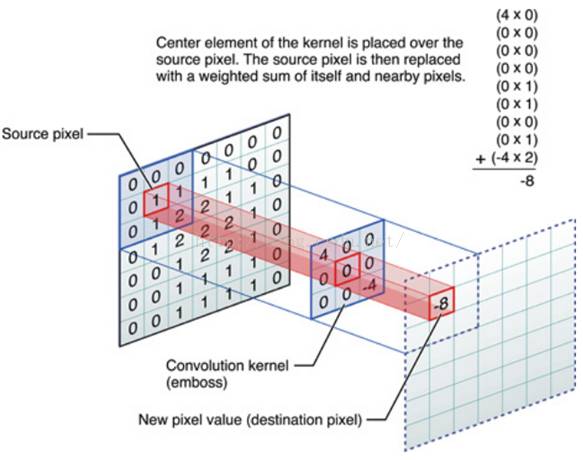
OK，举个具体的例子。比如下图中，图中左边部分是原始输入数据，图中中间部分是滤波器filter，图中右边是输出的新的二维数据。
分解下上图
48.什么是CNN的池化pool层?
池化，简言之，即取区域平均或最大，如下图所示（图引自cs231n）
上图所展示的是取区域最大，即上图左边部分中 左上角2x2的矩阵中6最大，右上角2x2的矩阵中8最大，左下角2x2的矩阵中3最大，右下角2x2的矩阵中4最大，所以得到上图右边部分的结果：6 8 3 4。很简单不是？
49. 学梵高作画的原理是啥
梵高风格画的实验教程《教你从头到尾利用DL学梵高作画：GTX 1070 cuda 8.0 tensorflow gpu版》
原理看这个视频：NeuralStyle艺术化图片（学梵高作画背后的原理）。
50. 现在有 a 到 z 26 个元素， 编写程序打印 a 到 z 中任取 3 个元素的组合（比如 打印 a b c ，d y z等）
分析：
char a, b, c;
for(a = 'a'; a<='z'; a++)
for(b= a+1; b<='z'; b++)
for(c = b+1; c<='z'; c++)
printf("%c%c%c\n", a, b, c);
问题1：不可能出现 bac等。因为每次我多加了 1 看看嵌套的 for 有什么不同，但是题目要求只求组合不管顺序。
问题2：如果你要这么做 ，面试官必然会问 ，如果我要求 4 个字母的组合呢？（一脸懵逼状=。=）
思路：
我设想 a - z 每个字母给一个标记 0 或 1 ,如果为 1 的时候表示这个字符在组合中 ,如果为 0 那么表示这个字符不在组合中。
这样子，我们需要 26 个标记位。
这个时候我们会发现 ，当所有变量都在组合中时， 那么就是 26 个 1；当一个变量都不在集组合中时，就是 26 个 0。
我们把 26 个 1 和 26 个 0 看成数字，那么就是 0 和 (1 << 26) - 1。
那么其它的组合，肯定是 0 到 (1 << 26) - 1 之间的数字，对吧
比如
cba 就是 …0000000111
dcba 就是 …00000000001111
所以说 我们做一个循环 从 0 开始 到(1 << 26) - 1
然后只取有 3 个 1 的数字
然后再看对应的 1 代表哪个字符就可以了
具体就要看程序了：
#include
//某个数二进制位上有几个 1
int bit(unsigned int x)
{
int c = 0;
while( x )
{
c++;
x = (x & (x - 1));
}
return c;
}
void print(unsigned int x, int count)
{
int i = 0;
//控制，假如count为3， x 里边有三个 1
if( bit(x) == count )
{
for(i=0; i<26; i++)
{
if( x & 1)
{
printf("%c ", (char)('a' + i));
}
x = (x >> 1);
}
printf("\n");
}
}
int main()
{
const unsigned int N = 26;
const unsigned int C = 3;
const unsigned int X = (1 << N) - 1; //X=(1<<26)-1
unsigned int i = 0;
for(i=0; i 参考：http://blog.csdn.net/lvonve/article/details/53320680
