数据分析介绍之三——单变量数据观察之核密度估计

数据分析介绍之三——单变量数据观察之核密度估计

一、核密度估计

上一篇结尾处谈到了直方图的几个缺点，幸运的是，除了这些问题之外，还有经典直方图的替代方案。 称为核密度估计。

内核密度估计（KDEs）是一种比较新的技术。 与直方图和许多其他经典数据分析方法相比，它们几乎要求合理的现代计算机的计算能力有效。 即使是相当适中的数据集，它们也不能用纸和铅笔手工完成。 （有趣的是，计算和图形功能的可访问性如何能够新的方式来思考数据！）

为了形成KDE，我们在每个数据点的位置放置一个内核，即一个平滑的，强峰值的函数。 然后，我们将来自所有内核的贡献加起来，获得一个平滑的曲线，我们可以在x轴的任意点进行评估。

图2-4显示了一个例子。 这是我们以前在图2-1中看到的数据集的另一个表示。 虚线框是数据集的直方图（bin宽度等于1），实线是具有不同带宽的相同数据集的两个KDE（稍后将解释此概念）。 单个内核函数的形状可以清楚地看出来——例如，通过考虑低于20的三个数据点。您还可以看到最终曲线如何由单个内核组成，特别是当您查看30到40之间的点。

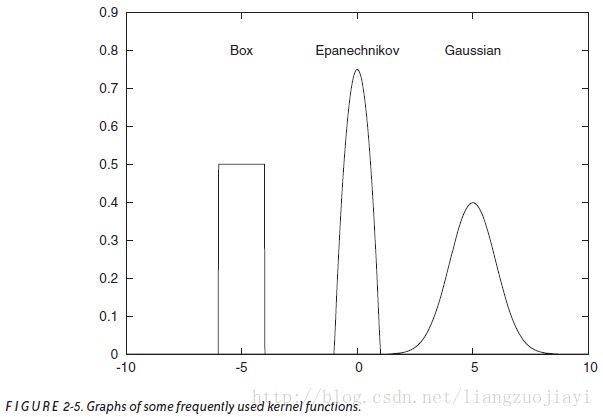
我们可以使用任何平滑，强峰值的函数作为内核，只要它集成到1; 换句话说，由单个内核形成的曲线下面积必须为1.（这是必要的，以确保生成的KDE正确归一化）。常用内核函数的一些示例包括（见图2-5）：

盒内核和Epanechnikov内核在有限范围之外为零，而高斯内核在任何地方都非零，但在有限域外可忽略不计。 事实证明，KDE产生的曲线并不依赖于内核函数的特定选择，所以我们可以自由地使用最方便的内核。 因为它很容易使用，高斯内核是最广泛使用的。 （有关高斯函数的更多信息，请参阅附录B.）

构建KDE需要做的事情：首先，我们必须通过适当地移动内核来移动每个点的位置。 例如，函数K（x-xi）将在xi处具有峰值，而不是0.其次，我们必须选择内核带宽来控制内核函数的扩展。 为了确保曲线下面积保持不变，我们缩小宽度，我们必须使曲线更高（如果我们增加宽度，则降低）。 带宽h的移位，重新缩放的内核函数的最终表达式是：

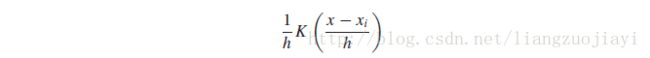
该函数在xi处具有峰值，其宽度约为h，其高度使得曲线下方的面积仍为1.图2-6显示了使用高斯核的一些示例。 请记住，所有三条曲线下的区域是相同的。

使用这个表达式，我们现在可以为任意数据集{x1，x2，…的带宽h写出KDE的公式。。。 ，xn}。 可以对沿x轴的任何点x评估该公式：

所有这一切都是直接的，易于实现的任何计算机语言。 请注意，对于大型数据集（具有数千个点的数据集），所需的内核评估数量可能会导致性能问题，特别是如果函数D（x）需要针对许多不同的位置进行评估（即，许多不同的值 的x）。 如果这成为一个问题，您可能需要选择一个更简单的内核函数，或者如果距离x-xi远大于带宽h，则不评估内核。

一个策略是从形成KDE的内核函数与数据集的卷积的认识开始。 您现在可以进行内核和数据集的傅立叶变换，并利用傅里叶卷积定理。 这种方法适用于非常大的数据集，但不属于我们讨论的范围。

现在我们可以解释图2-4中的宽灰色线：它是一个带宽较大的KDE。 使用这么大的带宽使得不可能解析各个数据点，但它确实突出了更大或更小频率的整个周期。 您选择的带宽选择取决于您的目的。

刚刚描述的KDE类似于古典直方图，但是它避免了上述两个问题。 给定数据集和带宽，KDE是唯一的; 如果我们选择了一个平滑的内核函数，比如高斯函数，KDE也很顺利。

二、最佳宽度选择

我们还需要修复带宽。 这是另外两种不同的问题：它不仅仅是一个技术问题，可以通过更好的方法解决; 相反，这是一个与数据集本身有关的根本问题。 如果数据遵循顺利的分配，则更宽的带宽是适当的，但是如果数据遵循非常严重的分布，那么我们需要较小的带宽来保留所有相关细节。 换句话说，最佳带宽是数据集的属性，并告诉我们有关数据的性质。

那么我们如何选择一个最佳的带宽值呢？ 直觉上，问题很明确：我们希望带宽足够窄以保留所有相关细节，但足够宽，以致产生的曲线不会太“摆动”。这是在每个近似问题中产生的问题：平衡忠诚度 代表行为的简单性。 统计学家说“偏差方差权衡”。

为了具体化，我们必须为我们的近似误差定义一个具体的表达式，其中考虑到偏差和方差。然后，我们可以为最小化此错误的带宽选择一个值。对于KDE，普遍接受的度量是近似值和真实密度之间的“预期均方误差”。问题是我们不知道我们正在尝试逼近的真实密度函数，所以似乎不可能以这种方式计算（并最小化）错误。但是，已经开发了聪明的方法来取得进展。这些方法大致分为两类。首先，我们可以尝试找到偏差和方差的明确表达式。平衡它们导致必须用数值​​求解的方程，或者 - 如果我们进行额外的假设（例如，分布是高斯），甚至可以产生类似于斯科特规则的明确表达式（在讨论直方图时先前介绍）。或者，我们可以意识到，KDE是从原始集合点被选择的概率密度的近似值。因此，我们可以从这个近似值（即从KDE表示的概率密度）中选择点，并看看它们如何复制我们开始的KDE。现在我们改变带宽，直到我们找到最适合复制KDE的值：结果是对数据的“真实”带宽的估计。 （后一种方法称为交叉验证。）

虽然不是特别困难，但是这两种方法的细节都会导致我们太远，所以我将在这里跳过。 如果您有兴趣，则在本章末尾的参考资料之一中，您将无可挑剔。 但是请记住，这些方法可以找到相对于均方误差的最佳带宽，这往往过度强调偏差偏差，因此这些方法会导致相当窄的带宽和KDE似乎过于曲折。 如果您正在使用KDE生成图形，以获得直观的点分布可视化，那么您可能会更好地使用一些手动试验和错误以及目视检查。 最后，没有一个“正确的”答案，只有最适合的一个给定的目的。 此外，最适合开发直观的理解可能不是使特定数学量最小化的理解。

三、核密度估计Python实现

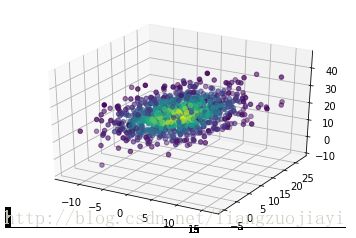
if __name__ == "__main__":  
    mu = np.array([1, 10, 20])  # 一维数组  
    sigma = np.matrix([[20, 10, 10], [10, 25, 1], [10, 1, 50]])   # 二维数组 协方差矩阵，该矩阵必须是对称而且是半正定的  
    data = np.random.multivariate_normal(mu, sigma, 1000)   # 产生样本点，第一个参数表示样本每维的均值，第二维表示维度之间的协方差，第三个表示产生样本的个数  
    values = data.T  
    kde = stats.gaussian_kde(values)  # 构造多变量核密度评估函数  
    density = kde(values)   # 给定一个样本点，计算该样本点的密度  

    # 可视化展现  
    fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))  
    x, y, z = values  
    ax.scatter(x, y, z, c=density)  
    plt.show()  

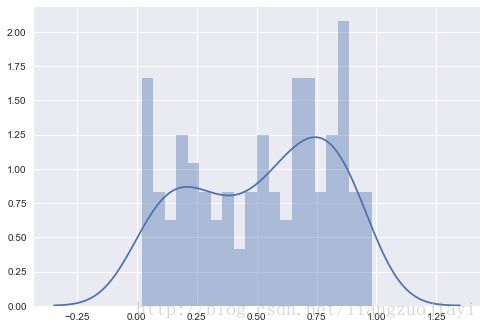
    print (data)

import seaborn 
x = np.random.rand(100)
seaborn.distplot(x, bins=20).get_figure()