pytorch实践(改造属于自己的resnet网络结构并训练二分类网络)

在学习pytorch过程中，突然想拥有属于自己的网络结构，于是便自己选择了一个比较简单的resnet18进行改造，并用其对蚂蚁和蜜蜂进行分类，比较一下没有经过预训练的resnet18好还是自己改造的resnet_diy好。

在开始撸代码之前，为了方便大家自己设计网络，我把resnet的pytorch实现详细的解读一遍。

ResNet

ResNet 解决了 deep NN 的两大问题：1. deep NN 的梯度弥散和爆炸问题；2. deep NN 的精度随着模型的加深，会逐渐饱和不再上升，甚至会大幅度下降。其算法原理简单的说，就是通过shorcut将远端的output与近端的output相连接，即H(x)=F(x)+x，以此来解决这两大问题。这个过程并没有严格的数学证明，大概因为shortcut可以很好的bp，详细了解请戳这里。

网络结构如上图所示，resnet有很多变形18/34/50/152。其中 ResNet 18/34 采用 Basic Block 作为基本单元，而 ResNet 50/101/152 则采用 Bottlenet Block 作为基本单元。

BasicBlock和Bottleneck

Basic Block就是左边的图，包括两个3×3的卷积操作。bollteneck是右边的图，为了减少参数，它采用了两个1×1的卷积。

Resnet18
ResNet 18/34 由 root block，stack 1-4 组成，每一个 stack 都由 Basic Block 叠加而成，所有 Basic Block 都采用 3×3 filter。其中，stack 1 每一层有64个 filter, stack 2 每一层有128个 filter，stack 3 每一层有256个 filter，stack 4 每一层有512个 filter。stack 1-4的数目，ResNet 18 为[2, 2, 2, 2]，ResNet 34 为[3, 4, 6, 3]。

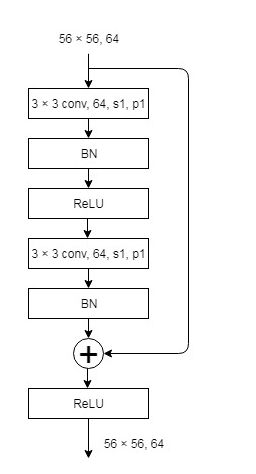
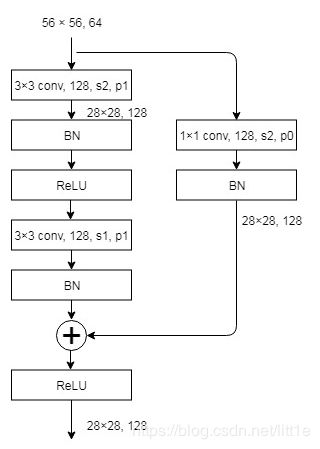
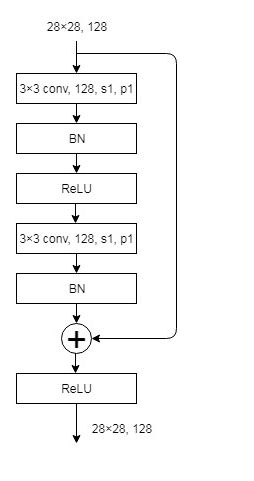
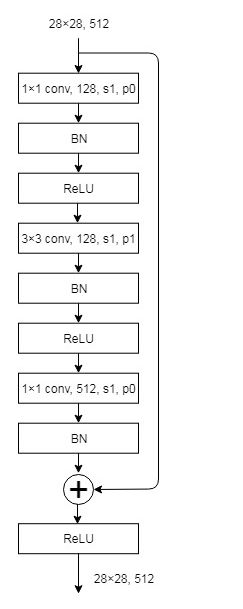
上面从左到右的顺序就是stack1-4的结构，第一个图是简单的卷积操作，并不涉及残差。

pytorch实现

下面我们对pytorch的实现进行详细解读。

class ResNet(nn.Module):

    def __init__(self, block, layers, num_classes=1000, zero_init_residual=False):
        super(ResNet, self).__init__()
        self.inplanes = 64
        self.conv1 = nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3,
                               bias=False)
        self.bn1 = nn.BatchNorm2d(64)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        self.layer1 = self._make_layer(block, 64, layers[0])
        self.layer2 = self._make_layer(block, 128, layers[1], stride=2)
        self.layer3 = self._make_layer(block, 256, layers[2], stride=2)
        self.layer4 = self._make_layer(block, 512, layers[3], stride=2)
        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
        self.fc = nn.Linear(512 * block.expansion, num_classes)

显而易见，我们的网络结构可以在代码中清晰的看出来，除了layer1-4，即残差部分的代码有疑惑外，其他结构应该看得很明白，那下面我们就残差部分来讲解。

 def _make_layer(self, block, planes, blocks, stride=1):
        downsample = None
        if stride != 1 or self.inplanes != planes * block.expansion:
            downsample = nn.Sequential(
                conv1x1(self.inplanes, planes * block.expansion, stride),
                nn.BatchNorm2d(planes * block.expansion),
            )

        layers = []
        layers.append(block(self.inplanes, planes, stride, downsample))
        self.inplanes = planes * block.expansion
        for _ in range(1, blocks):
            layers.append(block(self.inplanes, planes))

        return nn.Sequential(*layers)

class BasicBlock(nn.Module):
    expansion = 1

    def __init__(self, inplanes, planes, stride=1, downsample=None):
        super(BasicBlock, self).__init__()
        self.conv1 = conv3x3(inplanes, planes, stride)
        self.bn1 = nn.BatchNorm2d(planes)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(planes, planes)
        self.bn2 = nn.BatchNorm2d(planes)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        identity = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)

        if self.downsample is not None:
            identity = self.downsample(x)

        out += identity
        out = self.relu(out)

        return out

首先弄懂几个参数意义，inplanes 是提供给block的通道数，planes表示block的输出通道。大家知道，在做残差相加的时候，我们必须保证残差的维度与真正输出的维度相等（注意这里维度是宽高以及深度）这样我们才能把它们堆到一起，所以程序中出现了降采样操作。

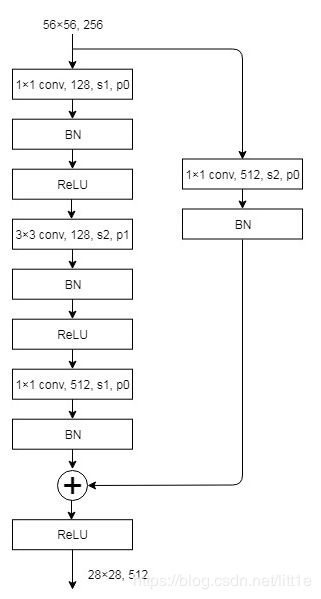
if stride != 1 or self.inplanes != planes * block.expansion:大家注意到这个if语句，它存在两种条件使他为真。第一就是stride != 1，我们以下图为例，输入56×56×256输出为28×28×512，显然，stride=2（resnet没有pooling）这时我们满足第一个条件，所以进入降采样操作，令stride=2，这样我的残差输出就变成了28×28。

再看第二个条件 self.inplanes != planes * block.expansion,这是self.inplanes=256，而planes =512（这里因为basic block，block.expansion=1），所以第二个条件满足，那么进行降采样用1×1卷积改变通道数。
总之，这个步骤就是为了匹配维度。

BatchNorm2d
我们每一层都进行了BN，这里简单介绍一下，为了减小Internal Covariate Shift，对神经网络的每一层做归一化不就可以了，假设将每一层输出后的数据都归一化到0均值，1方差，满足正太分布，但是，此时有一个问题，每一层的数据分布都是标准正太分布，导致其完全学习不到输入数据的特征，因为，费劲心思学习到的特征分布被归一化了，因此，直接对每一层做归一化显然是不合理的。
但是如果稍作修改，加入可训练的参数做归一化，那就是BatchNorm实现的了，接下来结合下图的伪代码做详细的分析：

之所以称之为batchnorm是因为所norm的数据是一个batch的，
1.先求出此次批量数据xxx的均值
2.求出此次batch的方差
3.接下来就是对xxx做归一化
4.最重要的一步，引入缩放和平移变量 ,计算归一化后的值
接下来详细介绍一下这额外的两个参数，之前也说过如果直接做归一化不做其他处理，神经网络是学不到任何东西的，但是加入这两个参数后，事情就不一样了，先考虑特殊情况下，如果γ和β分别等于此batch的标准差和均值，那么yi不就还原到归一化前的x了吗，也即是缩放平移到了归一化前的分布，相当于batchnorm没有起作用，β 和γ分别称之为 平移参数和缩放参数 。这样就保证了每一次数据经过归一化后还保留的有学习来的特征，同时又能完成归一化这个操作，加速训练。

其实就是对γ，β反向BP来优化它们。

DIY resnet

我的想法其实很简单，就是在Resnet18的每个block中加一个1×1的卷积，让它的非线性更加丰富，这样网络的表达能力应该可以更好。其实没啥现实意义纯属娱乐。

class BasicBlock(nn.Module):
    expansion = 1

    def __init__(self, inplanes, planes, stride=1, downsample=None):
        super(BasicBlock, self).__init__()
        self.conv1 = conv1x1(inplanes, planes)  #+
        self.bn1 = nn.BatchNorm2d(planes)               #+
        self.conv2 = conv3x3(planes, planes, stride)
        self.bn2 = nn.BatchNorm2d(planes)
        self.relu = nn.ReLU(inplace=True)
        self.conv3 = conv3x3(planes, planes)
        self.bn3 = nn.BatchNorm2d(planes)
        #self.conv4 = conv1x1(planes, planes)
       # self.bn4 = nn.BatchNorm2d(planes)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        identity = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)

        out = self.conv3(out)
        out = self.bn3(out)
       # out = self.relu(out)

       # out = self.conv4(out)
       # out = self.bn4(out)

        if self.downsample is not None:
            identity = self.downsample(x)

        out += identity
        out = self.relu(out)

        return out

改的部分就这些，大家在理解了代码之后也可以试一试，还是很有成就感的。

我的主要思想：用未训练的resnet18（需要将它的模型稍微改变一下，因为原来的模型是在imagenet数据集上训练的，而我们是简单的蜜蜂和蚂蚁的二分类），改造如下：

model_ft = models.resnet18(pretrained=False)
num_ftrs = model_ft.fc.in_features
model_ft.fc = nn.Linear(num_ftrs, 2)

model_ft = model_ft.to(device)

criterion = nn.CrossEntropyLoss()

# Observe that all parameters are being optimized
optimizer_ft = optim.SGD(model_ft.parameters(), lr=0.001, momentum=0.9)

# Decay LR by a factor of 0.1 every 7 epochs
exp_lr_scheduler = lr_scheduler.StepLR(optimizer_ft, step_size=7, gamma=0.1)
model_ft = train_model(model_ft, criterion, optimizer_ft, exp_lr_scheduler,
                      num_epochs=25)

最终结果如下：

DIY的效果优于resnet18。
代码请参考https://github.com/guxiaowei1/DIYresnet-NST