万字总结复杂而奇妙的高斯过程!
高斯过程的理论知识
非参数方法的基本思想
高斯过程的基本概念
高斯过程的Python实现
使用Numpy手动实现
使用`Scikit-learn`实现高斯过程
小结
高斯过程GaussianProcess
高斯过程的理论知识
非参数方法的基本思想
在监督学习中,我们经常使用包含参数 的参数模型:
来解释数据,并通过 最大似然估计(MLE) 或 最大后验估计(MPE) 来推断参数 的最优值。
如果需要,我们还可以推断出一个完整的后验分布
来代替点估计 。
随着数据复杂性的增加,通常需要使用具有更多参数的模型来合理地解释数据。在非参数方法中,参数的数量取决于数据集的大小。
例如,在Nadaraya-Watson 核回归(Kernel regression) 中,将权重 分配给每个观察到的目标 ,并且为了预测新点 的目标值,将计算加权平均值:
这里,我们假设了接近 的观测值比远离 的观测值具有更高的权重。权重是使用核函数 根据 与观察到的 来计算的。
一种特殊情况是k最近邻(KNN),其中最接近 的 个观测值的权重为 ,所有其他观测值的权重为0。
非参数方法通常需要处理所有训练数据以进行预测,因此相比于参数方法,推断(inference)时速度较慢。另一方面,由于非参数模型仅需要记住训练数据,在这个层面上来说,训练速度通常会更快。
注1: 核回归是一种非参数回归的方法,这种模型是基于(特征 之间)特征越相似的则其所对应的 值也应该很相似,只不过引进了kernel函数来衡量特征之间的相似度;注2: 表示输入向量
高斯过程的基本概念
非参数方法的另一个示例是高斯过程(GPs)。参数方法需要推断参数的分布,而在非参数方法中,比如高斯过程,它可以直接推断函数的分布。
高斯过程定义了先验函数。观察到某些函数值后,可通过代数运算以将其转换为后验函数。
在这种情况下,连续函数值的推断称为GP回归,但GP也可以用于分类。
高斯过程是一种随机过程,其为任意点 分配一个随机变量 ,并且有限数量的这些变量 的联合分布就是高斯分布(即正态分布):
在这里
并且 是均值函数,通常使用 ,因为GP具有足够的灵活性来对任意均值建模。 是正定核函数或协方差函数。因此,高斯过程是函数的分布,其形状(平滑度等等性质)由核函数 决定。
这里有一个假设:
如果通过核函数将点 和 视为相似,则在这些点上的函数值 和 ,也可以视为类似。
观察到一些GP的先验 可以将其转换为GP后验 ,其中观测数据为 。在给定新输入 的情况下,后验可用于预测 :
其中 与 分别为后验预测分布的期望向量与协方差阵。
根据GP的定义,观测数据 和预测 的联合分布为:
给定 个训练数据和 个新输入数据的情况下,我们有:
其中 为 单位矩阵。
,
其中 为 矩阵。
其中 为 矩阵。
是 对角线上的噪声项,如果训练目标无噪声,则将其设置为零;如果观察到噪声,则将其设置为大于零的值。为了简化符号,我们将平均值设置为0。可以使用公式[1]、[3]来计算后验预测分布的充分统计量:
这是实现高斯过程并将其应用于回归问题所需的最低知识。下一部分将展示如何从头开始使用纯NumPy实现GP,随后的部分将展示如何使用scikit-learn中的GP实现。
高斯过程的Python实现
使用Numpy手动实现
定义核函数
在这里,我们将使用平方指数内核squared exponential kernel,也称为高斯内核或RBF内核:
长度参数 控制函数的平滑度,而 控制垂直方向的波动性(在二维坐标系中可以理解为也就是纵坐标的波动性)。为简单起见,我们对所有输入维度(各向同性内核isotropic kernel)使用相同的长度参数 。
import numpy as np
def kernel(X1, X2, l=1.0, sigma_f=1.0):
'''
各向同性平方指数内核.
计算点X1与点X2的协方差矩阵.
Args:
X1: ndArray, m个点 (m x d).
X2: ndArray, n个点 (n x d).
返回:
协方差矩阵 (m x n).
'''
sqdist = np.sum(X1**2, 1).reshape(-1, 1) + np.sum(X2**2, 1) - 2 * np.dot(X1, X2.T)
return sigma_f**2 * np.exp(-0.5 / l**2 * sqdist)
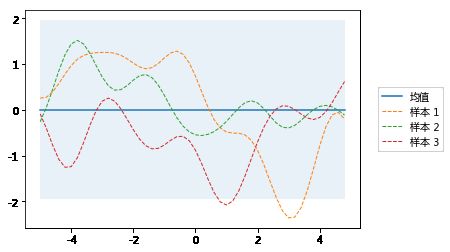
定义先验
我们首先定义一个均值 0 和一个用内核参数 和 计算的协方差矩阵的先验函数。
为了从该GP提取随机函数,我们从相应的多元高斯分布抽取随机样本。
以下示例绘制了三个随机样本,并将其与 0 均值和95%置信区间(根据协方差矩阵的对角线计算)一起绘制。
# 编写绘图函数
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
def plot_gp(mu, cov, X, X_train=None, Y_train=None, samples=[]):
X = X.ravel()
mu = mu.ravel()
uncertainty = 1.96 * np.sqrt(np.diag(cov))
plt.fill_between(X, mu + uncertainty, mu - uncertainty, alpha=0.1)
plt.plot(X, mu, label='均值')
for i, sample in enumerate(samples):
plt.plot(X, sample, lw=1, ls='--', label=f'样本 {i+1}')
if X_train is not None:
plt.plot(X_train, Y_train, 'rx')
plt.legend(bbox_to_anchor=(1.04,0.5), loc="center left")
def plot_gp_2D(gx, gy, mu, X_train, Y_train, title, i):
ax = plt.gcf().add_subplot(1, 2, i, projection='3d')
ax.plot_surface(gx, gy, mu.reshape(gx.shape), cmap=cm.coolwarm, linewidth=0, alpha=0.2, antialiased=False)
ax.scatter(X_train[:,0], X_train[:,1], Y_train, c=Y_train, cmap=cm.coolwarm)
ax.set_title(title)
%matplotlib inline
# 有限个输入数据点
X = np.arange(-5, 5, 0.2).reshape(-1, 1)
# 先验的均值与方差
mu = np.zeros(X.shape)
cov = kernel(X, X)
# 从先验分布(多元高斯分布)中抽取样本点
samples = np.random.multivariate_normal(mu.ravel(), cov, 3)
# 画出GP的均值, 置信区间
plot_gp(mu, cov, X, samples=samples)
基于无噪声训练数据进行预测
为了计算充分统计量,即后验预测分布的均值和协方差矩阵,我们用下面代码实现公式(4)和(5)
# 倒入计算逆矩阵的函数inv()
from numpy.linalg import inv
def posterior_predictive(X_s, X_train, Y_train, l=1.0, sigma_f=1.0, sigma_y=1e-8):
'''
计算后验分布的充分统计量
给定 m 个训练数据 X_train 与 Y_train
给定 n 个新输入数据 inputs X_s.
Args:
X_s: 新输入数据 (n x d).
X_train: 训练输入数据 (m x d).
Y_train: 训练输出数据 (m x 1).
l: 核函数的长度参数.
sigma_f: 核函数的纵向波动参数.
sigma_y: 噪音参数.
返回:
后验均值向量 (n x d) 与协方差矩阵 (n x n).
'''
K = kernel(X_train, X_train, l, sigma_f) + sigma_y**2 * np.eye(len(X_train))
K_s = kernel(X_train, X_s, l, sigma_f)
K_ss = kernel(X_s, X_s, l, sigma_f) + 1e-8 * np.eye(len(X_s))
K_inv = inv(K)
# 公式 (4)
mu_s = K_s.T.dot(K_inv).dot(Y_train)
# 公式 (5)
cov_s = K_ss - K_s.T.dot(K_inv).dot(K_s)
return mu_s, cov_s
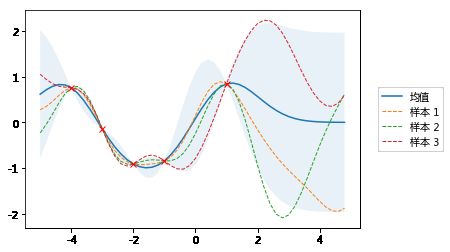
并将它们应用于无噪声训练数据X_train和Y_train。以下示例从后验预测中提取3个样本,并将它们与均值,置信区间和训练数据一起绘制。在无噪声模型中,训练点的方差为 0
注: 从后验预测分布提取的所有随机函数都经过训练点。
# 无噪音的5个输入数据
X_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1)
# y=sin(x)
Y_train = np.sin(X_train)
# 计算后验预测分布的均值向量与协方差矩阵
mu_s, cov_s = posterior_predictive(X, X_train, Y_train)
# 从后验预测分布中抽取3个样本
samples = np.random.multivariate_normal(mu_s.ravel(), cov_s, 3)
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train, samples=samples)
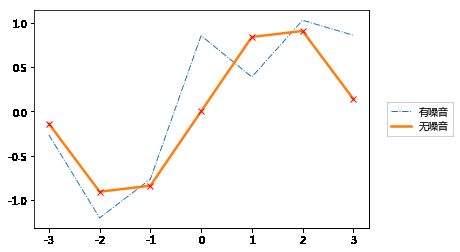
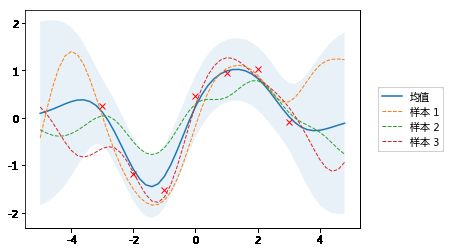
基于带有噪音的训练数据进行预测
如果模型中包含一些噪声,则仅对训练点进行近似,并且训练点的方差不为零。
# 定义噪音参数
noise = 0.4
# 带有噪音的训练数据
X_train = np.arange(-3, 4, 1).reshape(-1, 1)
Y_train = np.sin(X_train) + noise * np.random.randn(*X_train.shape)
# 可以对比地看一下带噪音的训练数据与不带噪音的训练数据的区别
plt.figure()
plt.plot(X_train, np.sin(X_train) + noise * np.random.randn(*X_train.shape), lw=1, ls='-.', label='有噪音')
plt.plot(X_train, np.sin(X_train) + 0.0 * np.random.randn(*X_train.shape), lw=2.5, ls='-', label='无噪音')
plt.plot(X_train, np.sin(X_train) + 0.0 * np.random.randn(*X_train.shape), 'rx')
plt.legend(bbox_to_anchor=(1.04,0.5), loc="center left")
plt.show()
# 计算后验预测分布的均值向量以及方差矩阵
mu_s, cov_s = posterior_predictive(X, X_train, Y_train, sigma_y=noise)
# 从后验预测分布中抽取3个样本点
samples = np.random.multivariate_normal(mu_s.ravel(), cov_s, 3)
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train, samples=samples)
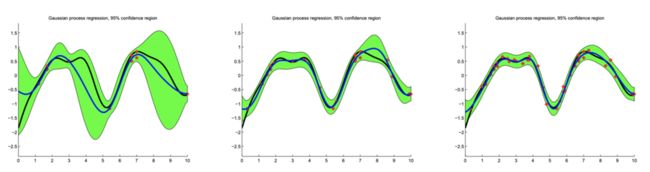
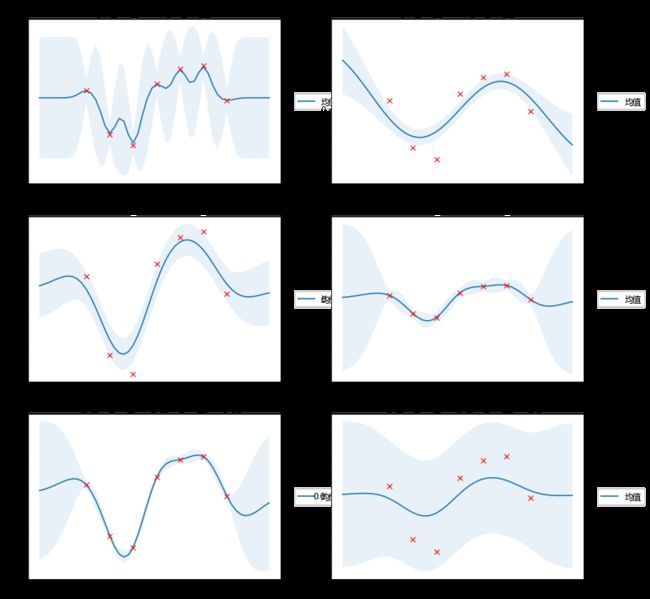
核函数参数和噪声参数的影响
以下示例显示了核函数参数 和 以及噪声参数 的影响。
值越高,函数越平滑,因此训练数据的近似值越粗糙(与真实值误差更大)。较低的 值使训练数据点之间的置信区间较宽,使函数更不平稳,波动更大。(下图第一行)
控制从GP提取的函数的垂直方向的波动性。 (下图第二行)
表示训练数据中的噪声量。较高的 值会做出更粗略的近似,从而避免过度拟合噪声数据。(下图第三行)
params = [
(0.3, 1.0, 0.2),
(3.0, 1.0, 0.2),
(1.0, 0.3, 0.2),
(1.0, 3.0, 0.2),
(1.0, 1.0, 0.05),
(1.0, 1.0, 1.5),
]
plt.figure(figsize=(12, 5))
for i, (l, sigma_f, sigma_y) in enumerate(params):
mu_s, cov_s = posterior_predictive(X, X_train, Y_train, l=l,
sigma_f=sigma_f,
sigma_y=sigma_y)
plt.subplot(3, 2, i + 1)
plt.subplots_adjust(top=2)
plt.title(f'l = {l}, sigma_f = {sigma_f}, sigma_y = {sigma_y}')
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train)
这些参数的最优值可以通过最大化由[1] [3]给出的边际对数似然来得到:
在下面的代码中,我们将最小化负边际对数似然来获得核函数参数 和 的参数估计。注意,这里我们假设噪声参数 是已知参数。
from numpy.linalg import cholesky, det, lstsq
from scipy.optimize import minimize
def nll_fn(X_train, Y_train, noise, naive=True):
'''
基于给定数据X_train和Y_train以及噪声水平
返回一个可以计算负边际对数似然的函数
Args:
X_train: 训练输入 (m x d).
Y_train: 训练输出 (m x 1).
noise: Y_train的噪声水平.
naive: 如果 True 那么使用公式(7)来实现
如果 False 那么使用数值方法来实现
返回:
最小的目标对象
'''
def nll_naive(theta):
# 使用公式(7)来实现
# 与下面的nll_stable的实现相比在数值上不稳定
K = kernel(X_train, X_train, l=theta[0], sigma_f=theta[1]) + \
noise**2 * np.eye(len(X_train))
return 0.5 * np.log(det(K)) + \
0.5 * Y_train.T.dot(inv(K).dot(Y_train)) + \
0.5 * len(X_train) * np.log(2*np.pi)
def nll_stable(theta):
# 数值上更稳定,相比于nll_naive
K = kernel(X_train, X_train, l=theta[0], sigma_f=theta[1]) + \
noise**2 * np.eye(len(X_train))
L = cholesky(K)
return np.sum(np.log(np.diagonal(L))) + \
0.5 * Y_train.T.dot(lstsq(L.T, lstsq(L, Y_train)[0])[0]) + \
0.5 * len(X_train) * np.log(2*np.pi)
if naive:
return nll_naive
else:
return nll_stable
# 求解可满足最小化目标函数的参数 l 及 sigma_f.
# 实际上,我们应该使用不同的初始化多次运行最小化,以避免局部最小化,
# 但是为了简单起见,此处将其跳过
res = minimize(nll_fn(X_train, Y_train, noise), [1, 1],
bounds=((1e-5, None), (1e-5, None)),
method='L-BFGS-B')
# 将优化结果存储在全局变量中,以便我们以后可以将其与其他实现的结果进行比较
l_opt, sigma_f_opt = res.x
# 使用优化的核函数参数计算后验预测分布的参数,并绘制结果图
mu_s, cov_s = posterior_predictive(X, X_train, Y_train, l=l_opt, sigma_f=sigma_f_opt, sigma_y=noise)
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train)

其最优化的核函数参数 和 的参数估计为
print(l_opt, sigma_f_opt)
0.9872536793237083 0.8613778055591963
更高维的高斯过程
以上实现也可以用于更高的输入数据维度。此处,GP用于拟合在 二维平面上扩展的正弦波的带噪声样本。
下图显示了核函数参数优化前后的带噪声样本和后验预测分布的均值向量。
#噪音参数
noise_2D = 0.1
rx, ry = np.arange(-5, 5, 0.3), np.arange(-5, 5, 0.3)
gx, gy = np.meshgrid(rx, rx)
X_2D = np.c_[gx.ravel(), gy.ravel()]
X_2D_train = np.random.uniform(-4, 4, (100, 2))
Y_2D_train = np.sin(0.5 * np.linalg.norm(X_2D_train, axis=1)) + \
noise_2D * np.random.randn(len(X_2D_train))
plt.figure(figsize=(14,7))
mu_s, _ = posterior_predictive(X_2D, X_2D_train, Y_2D_train, sigma_y=noise_2D)
plot_gp_2D(gx, gy, mu_s, X_2D_train, Y_2D_train,
f'参数优化前: l={1.00} sigma_f={1.00}', 1)
res = minimize(nll_fn(X_2D_train, Y_2D_train, noise_2D), [1, 1],
bounds=((1e-5, None), (1e-5, None)),
method='L-BFGS-B')
mu_s, _ = posterior_predictive(X_2D, X_2D_train, Y_2D_train, *res.x, sigma_y=noise_2D)
plot_gp_2D(gx, gy, mu_s, X_2D_train, Y_2D_train,
f'参数优化后: l={res.x[0]:.2f} sigma_f={res.x[1]:.2f}', 2)

使用Scikit-learn实现高斯过程
scikit-learn 提供了 GaussianProcessRegressor方法来实现GP回归模型. 你可以自定义核函数,或者使用它内置的核函数. 核函数也可以叠加. Squared exponential 核函数在scikit-learn中也就是RBF. scikit-learn中的RBF只有长度参数 。为了引入参数 ,我们需要将 RBF 与 ConstantKernel 复合。
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ConstantKernel, RBF
rbf = ConstantKernel(1.0) * RBF(length_scale=1.0)
gpr = GaussianProcessRegressor(kernel=rbf, alpha=noise**2)
# 1D 训练样本
gpr.fit(X_train, Y_train)
# 计算后验预测分布的均值向量与协方差矩阵
mu_s, cov_s = gpr.predict(X, return_cov=True)
# 获得最优核函数参数
l = gpr.kernel_.k2.get_params()['length_scale']
sigma_f = np.sqrt(gpr.kernel_.k1.get_params()['constant_value'])
# 与前面手写的结果比对
assert(np.isclose(l_opt, l))
assert(np.isclose(sigma_f_opt, sigma_f))
# 绘制结果
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train)

小结
从前面我们可以看出,与常见的机器学习模型不同,用高斯过程做预测的方法是直接生成一个后验预测分布(依然是高斯分布)。
这也决定了我们可以不仅仅得到一个“光秃秃”的预测值,还可以得到关于这个预测值的不确定性信息,可以利用这些信息绘制error-bar等等!
从统计学的角度上来看,利用高斯过程模型做预测具有很高的价值。
喜欢
分享
or