2016"百度之星" - 初赛(Astar Round2A)1001~1006
1001 All X
Problem Description:
F(x,m) 代表一个全是由数字x组成的m位数字。请计算,以下式子是否成立:
F(x,m) mod k ≡ c#include1002 Sitting in Line
Problem Description:
度度熊是他同时代中最伟大的数学家,一切数字都要听命于他。
现在,又到了度度熊和他的数字仆人们玩排排坐游戏的时候了。
游戏的规则十分简单,参与游戏的N个整数将会做成一排,
他们将通过不断交换自己的位置,最终达到所有相邻两数乘积的和最大的目的,
参与游戏的数字有整数也有负数。
度度熊为了在他的数字仆人面前展现他的权威,他规定某些数字只能在坐固定的位置上,
没有被度度熊限制的数字则可以自由地交换位置。状压DP
就是枚举放的顺序
#includescanf("%d%d",&A[i],&p[i]);
A[n]=0;
dp[0][n]=0;
for(int i=0;i<1<for(int j=0;j<=n;++j)
if(dp[i][j]!=-inf)
{
for(int k=0;kif(((i&1<0)&&(p[k]==-1||p[k]==c[i]))
{
dp[i|(1<1<int ans=-inf;
for(int i=0;i<=n;++i)
ans=max(ans,dp[(1<1][i]);
printf("Case #%d:\n",++Case);
printf("%d\n",ans);
}
return 0;
} 1003 Snacks
Problem Description:
百度科技园内有n个零食机,零食机之间通过n−1条路相互连通。
每个零食机都有一个值v,表示为小度熊提供零食的价值。
由于零食被频繁的消耗和补充,零食机的价值v会时常发生变化。
小度熊只能从编号为0的零食机出发,并且每个零食机至多经过一次。
另外,小度熊会对某个零食机的零食有所偏爱,要求路线上必须有那个零食机。
为小度熊规划一个路线,使得路线上的价值总和最大。
DFS序
线段树里每个节点保存的是从根节点与当前节点子树路径和的最大值…很奇妙
#pragma comment(linker, "/STACK:1024000000,1024000000")
#includeint u,v;
scanf("%d%d",&u,&v);
++u,++v;
add_edge(u,v);add_edge(v,u);
}
for(int i=1;i<=n;++i) scanf("%d",&A[i]);
dfs(1,-1);
build(1,n,1);
for(int i=1;i<=n;++i)
Update(In[i],Out[i],1,n,1,A[i]);
printf("Case #%d:\n",++Case);
while(m--)
{
int ope,x;
scanf("%d%d",&ope,&x);
++x;
if(ope==0)
{
int y;
scanf("%d",&y);
Update(In[x],Out[x],1,tim,1,y-A[x]);
A[x]=y;
}
else
{
LL ans=0;
ans+=Query(In[x],Out[x],1,tim,1);
printf("%lld\n",ans);
}
}
}
return 0;
} 1004 D Game
Problem Description
众所周知,度度熊喜欢的字符只有两个:B 和D。
今天,它发明了一个游戏:D游戏。
度度熊的英文并不是很高明,所以这里的D,没什么高深的含义,只是代指等差数列(等差数列百科)中的公差D。
这个游戏是这样的,首先度度熊拥有一个公差集合{D}{D},然后它依次写下NN个数字排成一行。游戏规则很简单:
在当前剩下的有序数组中选择X (X \geq 2)X(X≥2) 个连续数字;
检查11选择的XX个数字是否构成等差数列,且公差 d\in {D}d∈{D};
如果22满足,可以在数组中删除这XX个数字;
重复 1 - 31−3 步,直到无法删除更多数字。
度度熊最多能删掉多少个数字,如果它足够聪明的话?区间DP
有两种合并方式
1.[l,i]-[i+1,r]合并
2.跨区间合并,但是我们每次跨区间左右两边一共只要两个和三个,更多的可以通过区间DP的特性来完成,这样就每次记忆化搜索的时候就可以O(N)了
#include1,r));
dp[l][r]=tmp;
return tmp;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
Map.clear();
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
dp[i][j]=-inf;
for(int i=1;i<=n;++i) scanf("%d",&A[i]);
for(int i=1;i<=m;++i)
{
int x;
scanf("%d",&x);
Map[x]=true;
}
printf("%d\n",dfs(1,n));
}
return 0;
} 1005 BD String
Problem Description
众所周知,度度熊喜欢的字符只有两个:B和D。
今天,它发明了一种用B和D组成字符串的规则:
S(1)=BS(1)=B
S(2)=BBDS(2)=BBD
S(3)=BBDBBDDS(3)=BBDBBDD
…
S(n)=S(n-1)+B+reverse(flip(S(n-1))S(n)=S(n−1)+B+reverse(flip(S(n−1))
其中,reverse(s)reverse(s)指将字符串翻转,比如reverse(BBD)=DBBreverse(BBD)=DBB,flip(s)flip(s)指将字符串中的BB替换为DD,DD替换为BB,比如flip(BBD)=DDBflip(BBD)=DDB。
虽然度度熊平常只用它的电脑玩连连看,这丝毫不妨碍这台机器无与伦比的运算速度,
目前它已经算出了S(2^{1000})S(2^1000)的内容,但度度熊毕竟只是只熊,
一次读不完这么长的字符串。
它现在想知道,这个字符串的第LL位(从1开始)到第RR位,含有的BB的个数是多少?就是通过迭代来完成规律
先尽可能枚举我们已知的情况来加速,然后每次因为每次反转是有规律的
串A翻转完B的个数-D的个数==1,通过这个特性我们可以来缩小每个大于len到小于len的长度来迭代
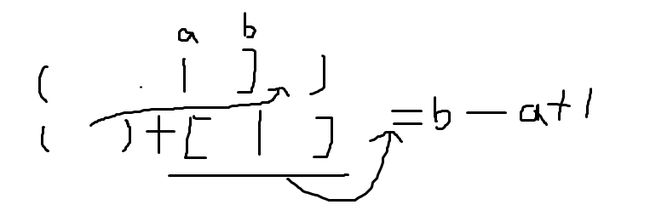
#include1]*2+1;
A[i]=len[i-1]+1;
}
}
LL solve(LL x)
{
if(x==0) return 0;
int k=1;
while(kif(len[k]==x) return A[k];
else
return solve(2*len[k]-x+1)+x-len[k];
}
int main()
{
init();
int T;
scanf("%d",&T);
while(T--)
{
LL l,r;
scanf("%lld%lld",&l,&r);
printf("%lld\n",solve(r)-solve(l-1));
}
return 0;
} 1006 Gym Class
Problem Description
众所周知,度度熊喜欢各类体育活动。
今天,它终于当上了梦寐以求的体育课老师。第一次课上,它发现一个有趣的事情。
在上课之前,所有同学要排成一列, 假设最开始每个人有一个唯一的ID,从1到NN,
在排好队之后,每个同学会找出包括自己在内的前方所有同学的最小ID,
作为自己评价这堂课的分数。麻烦的是,有一些同学不希望某个(些)同学排在他(她)前面,
在满足这个前提的情况下,新晋体育课老师——度度熊,
希望最后的排队结果可以使得所有同学的评价分数和最大。topsort+优先队列就OK了
#includeint a=0)
{
val=a;
}
};
priority_queueq;
vector<int>vec[maxn];
int top[maxn];
int A[maxn];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n,m;
memset(top,0,sizeof(top));
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) vec[i].clear();
for(int i=1;i<=m;++i)
{
int u,v;
scanf("%d%d",&u,&v);
vec[u].push_back(v);
top[v]++;
}
while(!q.empty()) q.pop();
for(int i=1;i<=n;++i)
if(top[i]==0) q.push(node(i));
int len=0;
while(!q.empty())
{
node cur=q.top();
q.pop();
int x=cur.val;
A[++len]=x;
int Size=vec[x].size();
for(int i=0;iif(top[vec[x][i]]==0) q.push(node(vec[x][i]));
}
}
int Max=inf;
LL Sum=0;
for(int i=1;i<=len;++i)
{
Max=min(Max,A[i]);
Sum+=Max;
}
printf("%lld\n",Sum);
}
return 0;
}