算法分析与设计基础 第二章谜题

习题2.1

4. a. 选择手套 在一个抽屉里有22只手套：5双红手套、4双黄手套和2双绿手套。你在黑暗中挑选手套，而且只能在选好以后才能检查它们的颜色。在最优的情况下，你最少选几只手套就能找到一双匹配的手套？在最差的情况下呢？

解答：最优情况：2只；最差情况：12只。

b. 丢失的袜子 假设在洗了5双各不相同的袜子以后，你发现有两只袜子找不到了。当然，你希望留下数量最多的袜子。因此，在最好的情况下，你会留下4双完整的袜子，而在最坏情况下，只会有3双完整的袜子。假设10只袜子中，每只丢失的概率都相同，请找出最佳情况的发生概率和最差情况的发生概率。在平均情况下，你能够指望留下几双袜子呢？

解答：

10. 象棋的发明

a. 根据一个著名的传说，国际象棋是许多世纪以前由一个印度西北部的贤人沙什发明的。当他把该发明献给国王的时候，国王很喜欢，就许诺可以给这个发明人任何他想要的奖赏。沙什要求以这种方式给他一些粮食：棋盘的第一个方格内只放1粒麦粒，第二格2粒，第三格4粒，第四格8粒，依次类推，直到64个方格全部放满。如果计算1粒麦粒需要1秒钟时间，那么计算完所有的格子的麦粒需要多长时间？

解答：t=1+2+4+……263=264-1≈1.84*10^19秒

b. 如果每个格子的麦粒数是前一个格子的麦粒数加2，那么计算完所有格子的麦粒将花费多长时间？

解答：t=1+3+5+……(2*64-1)=64*64=4096秒

 

习题2.2

11. 更轻或者更重？

你有n>2个外观相似的硬币和一个没有砝码的天平。其中一枚为假币，但并不知它比真币重还是轻。设计一个Θ(1)的算法来确定假币比真币重还是轻。

分析：题目只是要求确定假币比真币重还是轻，并不要求找出这枚假币，n的数量不确定(n>=3)，在绝大多数情况下只需在天平上比较两次即可知道假币的相对轻重，极端情况也只需三次。

解答：由于n>2，我们分两种情况解决：

情况一：n是3的整数倍。此时可以将这堆硬币按数量等分为三堆，设为A、B、C三堆，假币一定在其中一堆中。第一次在天平上比较A堆和B堆的重量。分为三种子情况：

a. A与B等重，则A、B堆均为真币，假币一定在C中。第二次比较A与C，若A比C重，则假币比真币轻，否则假币比真币重。

b. A比B重，则C堆一定全为真币，第二次比较A与C，若A与C等重，则假币在B中且假币比真币轻，若A比C重，则假币比真币重，若A比C轻，则假币比真币轻。

c. A比B轻，同情况b，C堆一定全为真币，第二次比较A堆与C堆，若A与C等重，则假币在B中且假币比真币重，若A比C重，则假币比真币重，若A比C轻，则假币比真币轻。

情况二：n不是3的整数倍。此时仍然可以将这堆硬币按数量等分为三堆A、B、C，多出来的1~2个硬币先放到一边。第一次在天平上比较A堆和B堆的重量。也分为三种子情况：

a. A与B等重，则A、B均为真币。第二次比较A与C，若A比C重，则假币一定在C中且假币比真币轻。若A比C轻，假币仍然一定在C中且假币比真币重。若A与C等重，则假币只能在放到一边的多出来的1~2个硬币中，A、B、C三堆均为真币。这种极端情况需要第三次用天平比较，将这1~2枚多出来的币与同等数量的真币比较，若同等数量的真币更重，则假币比真币轻，否则假币比真币重。

b. A比B重，则C堆一定全为真币，假币在A或B中。第二次比较A与C，若A与C等重，则假币在B中且假币比真币轻，若A比C重，则假币比真币重，若A比C轻，则假币比真币轻。

c. A比B轻，同子情况b，C堆一定全为真币，假币在A或B中。第二次比较A与C，若A与C等重，则假币在B中且假币比真币重，若A比C重，则假币比真币重，若A比C轻，则假币比真币轻。

 

12. 墙上的门 你面前是一堵朝两个方向无限延伸的墙。墙上有一扇门，但你并不知道门离你有多远，也不知道门位于哪个方向。你只有走到门面前才能看到它。假设从当前位置到门要走n步，请设计一个算法，使你最多走O(n)步就能遇到门。

分析：首先，以当前位置为原点，门距离原点有n步（n未知），而且门位于哪个方向也不知道，所以不能只朝一个方向去找，万一选错方向就永远找不到门了。只能像钟摆一样以原点为中心来回找。也不能每多走一步就往另一个方向走，因为这样找到门时已经走了2*(1+2+3+...+n)步，即n*(n+1)步，对应于O(n^2)复杂度，不满足题目要求。

解答：考虑 i 从0开始，先从原点出发向右走2^i步，返回原点，再向左走2^i步，再返回原点，接着向右走2^(i+1)步，返回原点，再向左走同样的2^(i+1)步...直到在途中找到门为止。由于门到原点的距离为n步，我们能找到一个整数k，使得2^(k-1) < n <= 2^k. 这样在找到门之前，你最多走了4*(2^0 + 2^1 + ... + 2^(k-1)) + 3*2^k 步，即4 * (2^k - 1) + 3 * 2^k < 7 * 2^k = 14 * 2^(k - 1) < 14 * n。这样就保证最多走O(n)步就能遇到门。

 

习题2.3

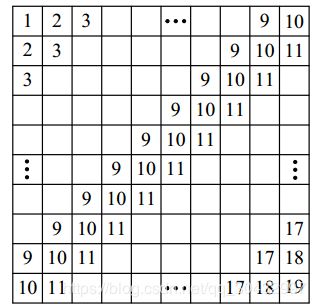
10. 心算数 如下图所示，在一个10*10的表格中，用相同数字在对应的对角线上填满，心算表格上所有数字之和。

解答：以数字10所在直线为对称轴，两边的数字加起来都是20，把每一个格子看成10，总和为1000.

 

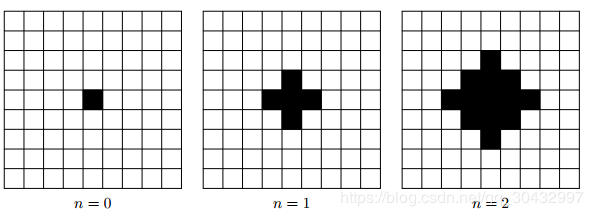
12. 冯·诺依曼邻居问题 考虑下列算法：从一个1*1的方格开始，每次都会在上次图形的周围再加上一圈方格，在第n次的时候要生成多少个方格？下图给出了n=0,1,2时的结果。

分析：n=0, 1个方格；n=1，5个方格；n=2，13个方格；n=3,  25个方格……在生成方格时发现比n-1时多了4条边，有两条边的格子数为n+1，有两条格子数为n-1，一共是4n。所求方格数为等差数列的和

解答：

 

13. 页面编号 假设页面从1开始连续编号，共有1000页。计算所有的页码中十进制数字的总个数。

分析：个位数字：1000；十位数字：1000-9=991；百位数字：1000-99=901，千位数字：1

解答：2893

 

习题2.4

5. 汉诺塔谜题

a. 汉诺塔谜题最早是由一个法国数学家卢卡斯于19世纪90年代提出的。当时的版本是这样的：当64个圆盘被从梵塔上移走时，世界末日也就来临了，如果祭司一分钟移动一个圆盘，请估计一下，移走全部圆盘一共需要多少年？

解答：分钟=≈3.51*10^13年

b. 在该算法中，要移动第i大的盘子一共需要移动多少步？

分析：在三个盘子情况下，从大到小的盘子分别移动了1、2、4次，因为每一次移动第i大盘子，都要先将第i+1大的盘子移走，然后移动第i大盘子，再把第i+1大的盘子移回来。所以次数为等比数列。

解答：2^(i-1)

c. 为汉诺塔谜题设计一个非递归的算法，并用你熟悉的语言实现。

非递归算法：定义从小到大的盘子序号分别为1，2，……n。可以用一个1到2n - 1的2进制序列可以模拟出n个盘子的汉诺塔过程中被移动的盘子的序号序列。即给定一个n，我们通过0到2n - 1序列可以判断出任意一步应该移动那个盘子。判断方法：第m步移动的盘子序号是m用二进制表示的最低位bit为1的位置。

证明： n = 1，显然成立。假设n = k 成立。n = k + 1时，对应序列1到2k+1 - 1，显然这个序列关于2k左右对称。假设我们要把k + 1个盘子从A移动C。那么2k可以对应着Move(k + 1, A, C)。 1 到 2k - 1 根据假设可以对应Hanoi(A, B, C, k), 定义 void Hanoi(char src, char des, char via, int n)表示把n个盘子从src上借助via移动到des上。至于2k + 1 到 2k + 1 - 1把最高位的1去掉对应序列变成1到2k - 1，显然2k + 1 到 2k + 1 - 1和1到2k - 1这两个序列中的对应元素的最低位bit为1的位置相同。因此2k + 1 到 2k + 1 - 1可以对应Hanoi(B, C, A, k)。所以对n = k + 1也成立。

下面讨论第m步应该移动对应的盘子从哪到哪？定义顺序为 A->B->C->A, 逆序为C->B->A->C。

性质: 对n个盘子的汉诺塔,任意一个盘子k(k <= n)k在整个汉诺塔的移动过程中要么一直顺序的，要么一直逆序的。而且如果k在n个盘子移动过程的顺序和k - 1(如果k > 1)以及k + 1(如果k < n)的顺序是反序。

比如：n = 3，其中1的轨迹A->C->B->A>C逆序，2的轨迹A->B->C顺序，3的轨迹A->C逆序

1 A->C

2 A->B

1 C->B

3 A->C

1 B->A

2 B->C

1 A->C

证明：假设n <= k成立。对于n = k + 1，根据递归算法，Hanoi(A，C，B，k + 1) = Hanoi(A, B, C, k) + Move(A, C, k + 1) + Hanoi(B，C，A，k);整个过程中盘子k + 1只移动一次A->C为逆序对应着2k。对于任意盘子m < k + 1,m盘子的移动由两部分组成一部分是前半部分Hanoi(A, B, C, k)以及后半部分的Hanoi(B, C，A，k)组成。显然如果m在Hanoi(A, C, B, k)轨迹顺序的话，则m在Hanoi(A, B, C, k)以及Hanoi(B, C，A，k)都是逆序。反之亦然。这两部分衔接起来就会证明m在Hanoi(A，C，B，k)和Hanoi(A，C，B，k + 1)中是反序的。同时有Hanoi塔中最大的盘子永远是逆序且只移动1步，A->C。

这样的话：m = k + 1，在Hanoi(A，C，B，k + 1)中是逆序。m = k，由于在Hanoi(A，C，B，k)中是逆序的，所以Hanoi(A，C，B，k + 1)中是顺序的。m = k - 1，由于在Hanoi(A，C，B，k - 1)是逆序的，所以Hanoi(A，C，B，k)是顺序的，所以Hanoi(A，C，B，k + 1)是逆序的。依次下去……结论得证。

总结：在n个汉诺中n， n - 2，n - 4……是逆序移动，n - 1， n - 3，n - 5……是顺序移动。

#include 
using namespace std;

int main()
{
int n;
cin >> n;
char order[2][256];
char pos[64];
for (int i = 0; i<64; i++)
{
pos[i] = 'A';    //初始的时候，所有的圆盘位置都是 'A';
}
order[0]['A'] = 'B';
order[0]['B'] = 'C';
order[0]['C'] = 'A';
order[1]['A'] = 'C';
order[1]['B'] = 'A';
order[1]['C'] = 'B';
//0是顺序 1是逆序
int index[64];
//确定轨迹的顺序还是逆序
int i, j, m;
for (i = n; i > 0; i -= 2)
index[i] = 1;
for (i = n - 1; i > 0; i -= 2)
index[i] = 0;
memset(pos, 'A', sizeof(pos));
for (i = 1; i < (1 << n); i++)
{
for (m = 1, j = i; j % 2 == 0; j /= 2, m++);  //计算出当前步骤序号的最低的 bit 为 1 的位置。
cout << m << " : " << pos[m] << " --> " << order[index[m]][pos[m]] << endl;
pos[m] = order[index[m]][pos[m]]; //更改当前位置
}
return 0;
}

12. 重温冯·诺依曼邻居问题 建立一个递推关系并求解，以计算n阶冯·诺依曼邻居的细胞数。

解答：如习题2.3.11所述，S(n)=S(n-1)+4n当n>0，S(0)=1，可以直接利用等差数列求和公式得到

 

13. 烤汉堡 有n个汉堡需要在烤架上烤，但是烤架上一次只能放2个汉堡。每个汉堡都需要两面烤，不管是烤一个汉堡还是同时烤两个汉堡，考好一个汉堡的一面用时1分钟。假设要在最短的时间内完成该任务，考虑下列递归算法。如果n<=2，一个汉堡单独烤并翻面，两个汉堡则同时烤并翻面。如果n>2，两个汉堡同时烤并翻面，然后给余下n-2个汉堡递归地应用同样的过程。

a. 给出该算法烤n个汉堡所需要的递推关系并求解。

解答：递推关系S(n)=S(n-2)+2当n>2，S(1)=S(2)=2。所以当n为偶数，S(n)=n；当n为奇数，S(n)=n+1；

b. 对于任意n>0个汉堡，该算法完成任务的时间并不是最少的，为什么？

解答：因为当n为大于1的奇数时，需要的最少时间可以是n分钟，比如当n=3时，先烤两个汉堡1分钟，然后换掉一个汉堡烤1分钟，最后再把未烤完的汉堡再烤1分钟。

c. 给出一个在最少时间内完成烤汉堡任务的正确递归算法。

解答：如前一问所述，当n为奇数且还剩下3个汉堡时，改变烤汉堡的方法，使得最后3个汉堡只需3分钟即可烤完。递推关系S(n)=S(n-2)+2当n>3，S(1)=S(2)=2，S(3)=3。

 

14. 名人问题 n个人中的名人是指这样一个人：他不认识别人，但是每个人都认识他。任务就是找出这样一个名人，但只能通过询问“你认识他/她吗？”这种问题来完成。设计一个高效算法，找出该名人或者确定人群中有没有名人。你的算法在最坏情况下需要问多少个问题。

解答：通过询问一个问题，每次减少一个人选。递归进行。对最后一人再询问一或两个问题确认。

第一步：从人群中选择两个人A和B。问A是否认识B。如果A认识B，删除A。如果A不认识B，删除B。

第二步：对剩下n-1个人递归进行上一步。

第三步：如果第二步结束后没有人，那就没有名人。如果剩下一人非A非B，是C，问C是否认识第一步中被删除的人。如果C说不认识，问第一步里被删除的人是否认识C。如果被删之人说认识，那么C是名人。其余情况皆是没有名人。如果剩下一人是B，问B是否认识A，如果B不认识，B是名人，否则没有名人。如果剩下一人是A，问B是否认识A，如果B认识，A是名人，否则没有名人。

在最差情况下：递推关系S(n)=S(n-1)+3当n>2，S(1)=0，S(2)=2。解得S(n)=2+3(n-2)当n>1，S(1)=0.

 

习题2.5

2. 斐波那契兔子问题 一个人把一对兔子用围墙围住。如果最初的一对兔子（一雌一雄）是新生的，并且所有的兔子在出生后的第一个月都不能繁殖，但是在之后的每个月末都能生出一对兔子（一雌一雄），那么一年后围墙里将会有多少对兔子？

解答：F(n)=F(n-1)+F(n-2)，当n>1。F(0)=F(1)=1。解得F(12)=233。共有233对兔子

 

3. 爬梯子 假设每一步可以爬一格或者两格梯子，爬一部n格梯子一共可以用几种方法？

解答：F(1)=1, F(2)=2, F(n)=F(n-1)+F(n-2)当n>2。可知F(n)=Fib(n+1)。

 

11. 分解斐波那契矩形 给定一个矩形，它的边长是两个连续的斐波那契数。设计一个算法来把它分解成正方形，且具有相同尺寸的正方形不超过两个。你的算法的时间效率类型是什么？

解答：不断地将两个边长数字相减，每次相减分割出一个正方形（边长为较小数），得到的数列即为逆序的斐波那契数列，算法的时间效率为θ(n)。