C++ STL LIST SORT 排序算法图解

最近看 <> 留意到上面说 std::list::sort 算法能做到 O(nlog2(n)) 复杂度，而直接对 std::list 套用 std::sort 只能做到 O(n²)

思考后发现如果把 std::sort 套到 std::list 上由于是 Bidirectional Iterator 的原因，计算距离的时候需要一步一步的移动，经典的 intro sort/quick sort 无法在这个双端链表的结构上面施展，而 heap sort 需要先 make_heap，双端链表由于无法快速定位到中间的元素，第一步的 make_heap 都很难操作。

参考了网上资料以及<> 发现，该排序算法使用的是类似 merge sort 的思想，代码比较简短，第一次看的时候不是很好理解，在此做个记录

一开始也排除了 merge sort, 因为传统的 merge sort 需要不停地对半，归并，对半，归并，在一个双端链表要怎么实现这个对半的过程呢?

这是 <> 上面的 list::sort 编辑过后的代码

#include 
#include 
#include 
template 
void pr_arr(const std::list &lst, std::string hint = "")
{
		std::cout << hint << ": ";
		for (const auto &i : lst)
		{
				std::cout << i << " ";
		}
		if (!lst.size())
				std::cout << "empty list";
		std::cout << std::endl;
}

template >
struct my_list: public std::list
{
		void my_sort()
		{
				std::ostringstream str_os;
				std::list carry;
				std::list counter[64];
				int fill = 0;
				std::list &base_lst = *this;
				while (! this->empty())
				{
						pr_arr(base_lst, "before splice, base");
						pr_arr(carry, "carry");
						carry.splice(carry.begin(), base_lst, this->begin());
						pr_arr(base_lst, "after splice, base");
						pr_arr(carry, "carry");
						int i = 0;
						while (i < fill && !counter[i].empty())
						{
								std::cout << "i: " << i << " fill: " << fill << "\n";
								counter[i].merge(carry);
								std::cout << "after counter[i].merge(carry)\n";
								pr_arr(counter[i], "counter[i]");
								pr_arr(counter[i+1], "counter[i+1]");
								pr_arr(carry, "carry");
								carry.swap(counter[i++]);
						}
						std::cout << "\ni: " << i << " before carry.swap(counter[i]) " << std::endl;
						pr_arr(counter[i], "counter[i]");
						pr_arr(carry, "carry");
						carry.swap(counter[i]);
						std::cout << "i: " << i << " after carry.swap(counter[i]) " << std::endl;
						pr_arr(counter[i], "counter[i]");
						pr_arr(carry, "carry");
						if (i == fill) ++fill;
				}
				for (int i = 1; i < fill; ++i)
				{
						std::cout << "i: " << i << "fill: " << fill << "\n";
						pr_arr(counter[i], "counter[i] before merge i - 1");
						counter[i].merge(counter[i-1]);
						pr_arr(counter[i], "counter[i] after merge i - 1");
				}
				this->swap(counter[fill-1]);
		}
};

int main()
{
		my_list m;
		m.push_back(3);
		m.push_back(5);
		m.push_back(4);
		m.push_back(1);
		m.push_back(2);
		pr_arr(m, "before my_sort\n\n\n");
		m.my_sort();
		pr_arr(m, "\n\n\nafter my_sort");
		return 0;
}

配合程序里的输出，大概理解了如何对双端链表进行排序

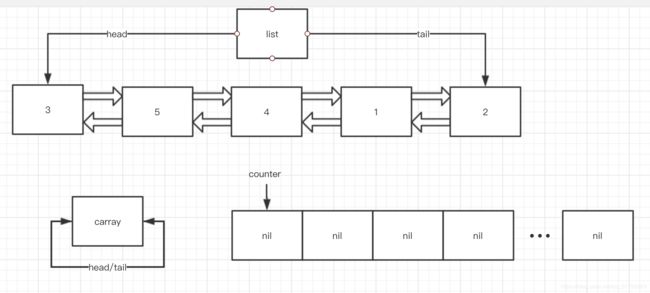
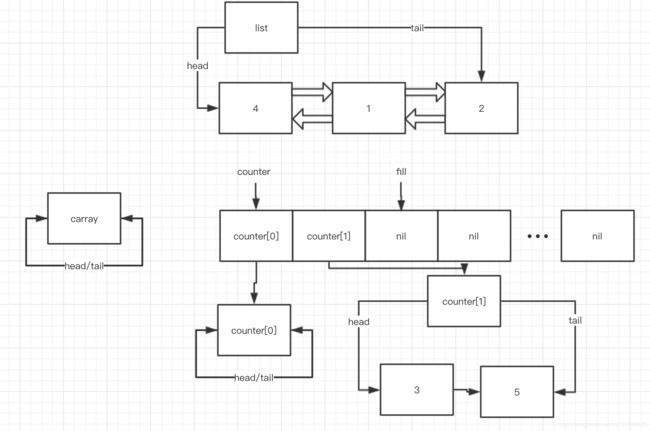
第一次 while (! this->empty()) 循环之前是这样的

第一次 splice 之后:

此时 i = 0, fill = 0, i < fill 不成立, 直接跳过中间的 while, 进入到下面部分 carry 和 counter[0] 进行 swap, 此时

 

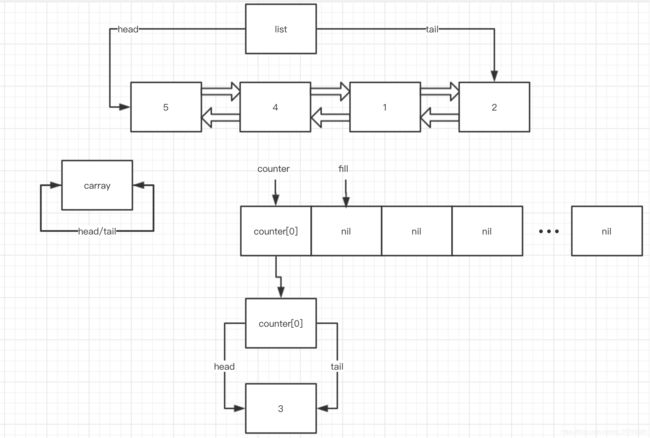
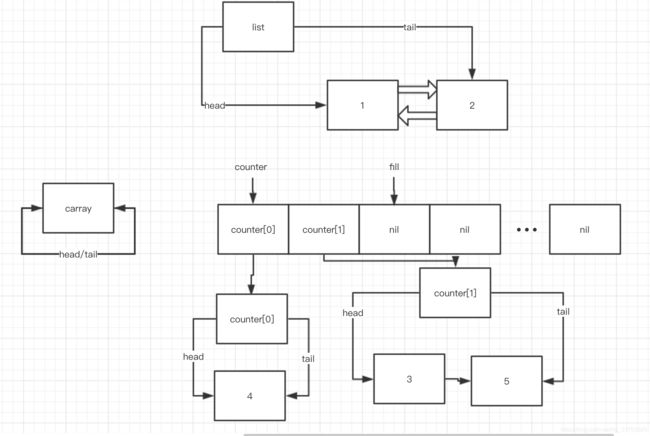
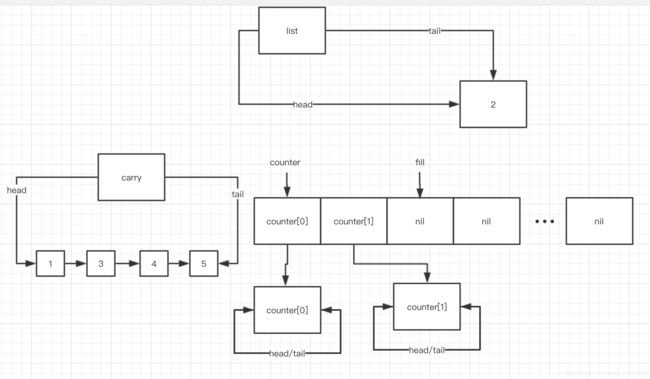
第二次 while (! this->empty()) 循环, splice 之后:

此时, i = 0, fill = 1, counter[0] 不为空，进入 while (i < fill && !counter[i].empty()) 中，这是刚进入的这个 while block 第一次结束前的状态

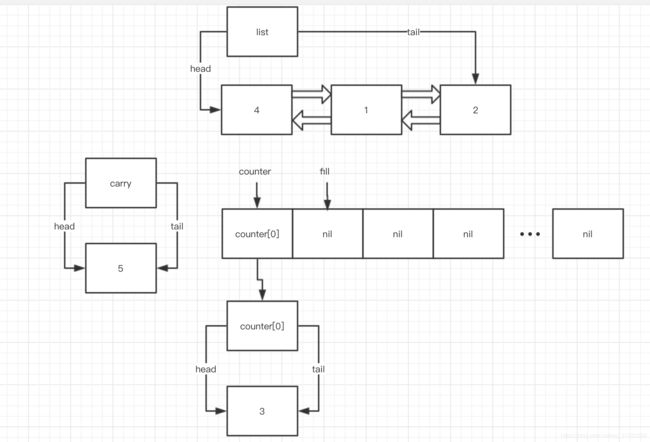
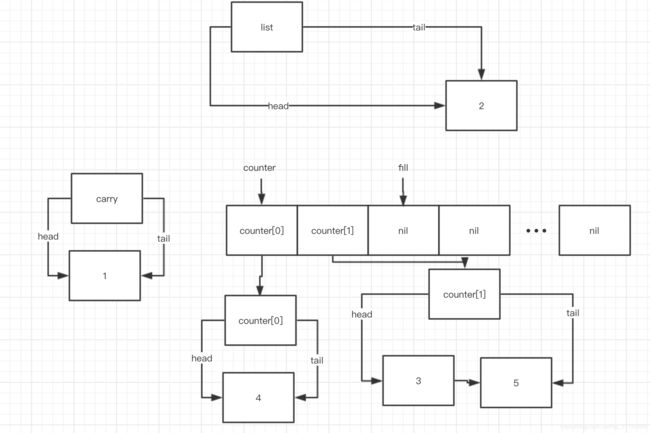
此时, i = 1, carry 刚用 swap 把 counter[0] merge 之后的内容换了出来，如上图所示，而 fill 也 为 1, 和 i 的值相同，所以这个 while block 执行一次就完成了，下面是 ++fill 这一句之后的状态

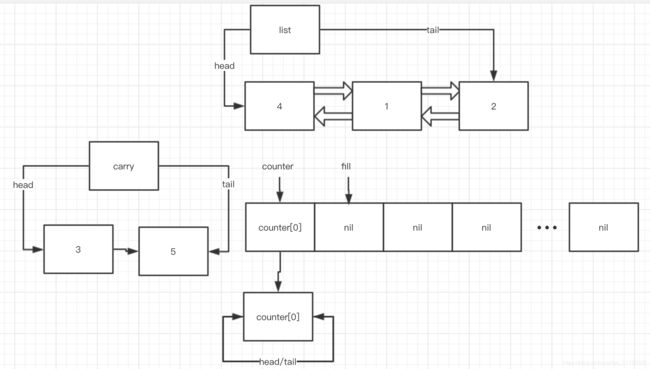
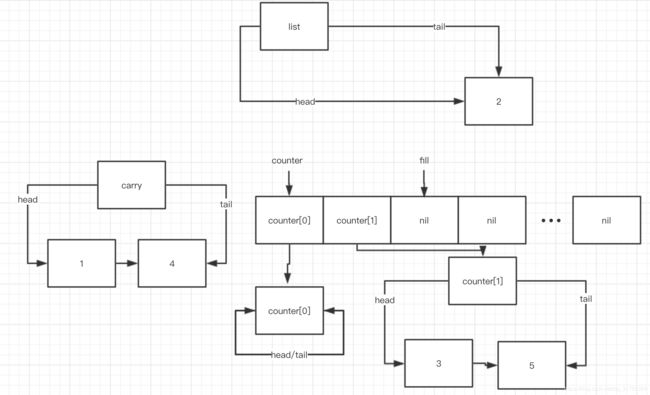
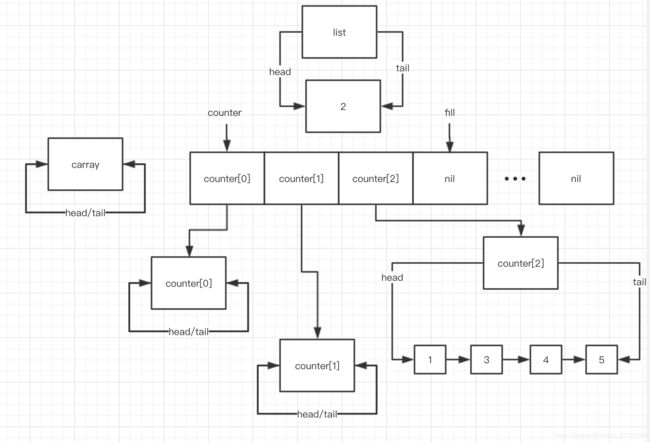
第三次 while (! this->empty()) 循环, splice 之后:

此时, i = 0, fill = 2, counter[0] 为空，while (i < fill && !counter[i].empty()) 不符合，故不会进入block, 下面是 if (i == fill) ++fill 之后的状态

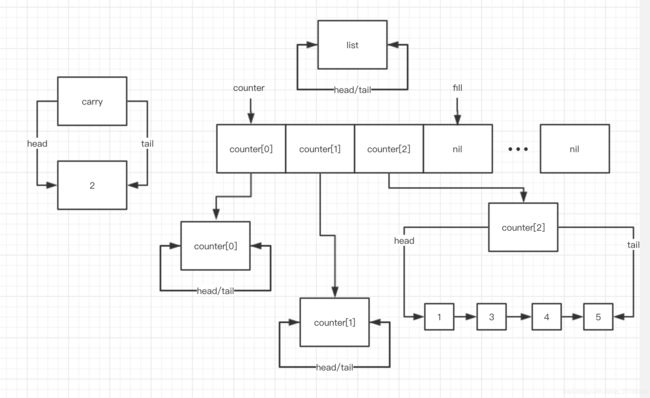
第四次 while (! this->empty()) 循环, splice 之后:

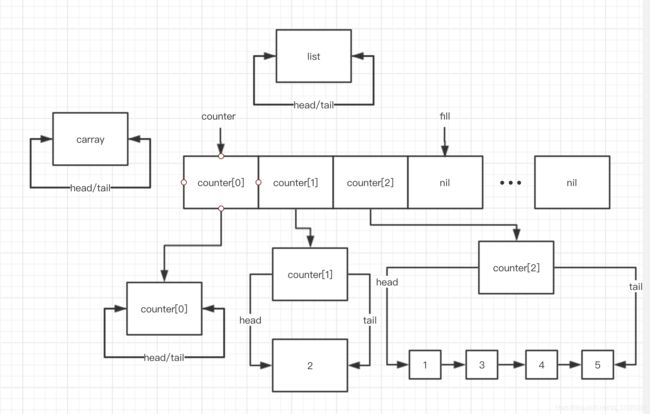
此时, i = 0, fill = 2, counter[0] 不为空，进入 while (i < fill && !counter[i].empty()) , 该 while block 第一次结束前状态

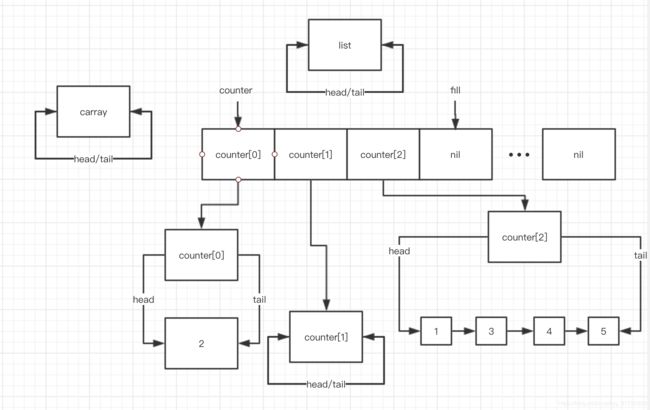
第二次进入 while (i < fill && !counter[i].empty()) , 此时, i = 1, fill = 2, counter[1] 不为空，结束前:

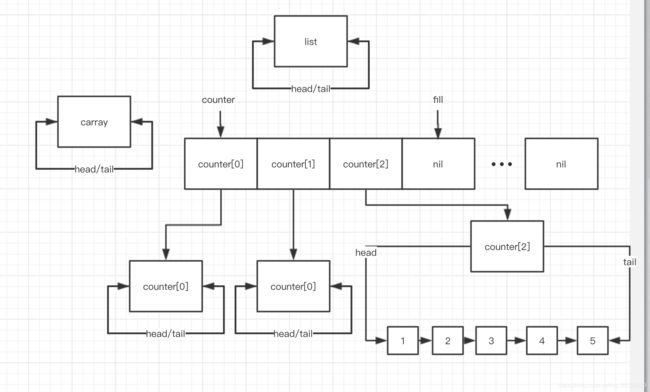
此时 i = 2, fill = 2, 结束 while (i < fill && !counter[i].empty()) 循环，这是 if (i == fill) ++fill; 之后的状态:

最后一次 while (! this->empty()) 循环, splice 之后:

此时, i = 0, fill = 3, counter[0] 为空，不会进入 while (i < fill && !counter[i].empty()) , 这是 if (i == fill) ++fill; 之后的状态:

此时, while (! this->empty()) 结束，进入 如下循环

for (int i = 1; i < fill; ++i)
{
        counter[i].merge(counter[i-1]); 
}

i = 1 结果:

 

i = 2 结果:

最后，再把 list 和 counter[2] swap 一次，就大功告成了

简单来说，就是每凑成 2的平方个元素，就进行一次 merge, 总共进行 log2(n) 次 merge, 每次 merge 进行 n(实际上是2, 4, 8, 16... 次) 次操作，得出时间复杂度为 O(nlog2(n))