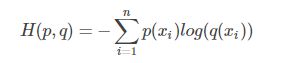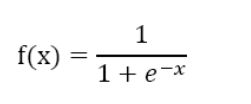yolov3中loss函数的探索（一）：ori-darknet、giou-darknet

yolov3中loss函数的探索

知识补丁

1.交叉熵

（p(xi)：真实分布概率；q(xi)：预测分布概率）

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，由于KL散度中的前一部分熵不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

交叉熵是用来评估当前训练得到的概率分布与真实分布的差异情况。
它刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。

详情请参考：https://blog.csdn.net/tsyccnh/article/details/79163834

2.MSE：

均方误差loss函数：是求一个batch中n个样本的n个输出与期望输出的差的平方的平均值。

3.激活函数与loss函数的关系

softmax激活函数应用于多类分类–categorical_crossentropy交叉熵损失函数

softmax激活函数：

categorical_crossentropy交叉熵损失函数：

假设神经网络模型的最后一层的全连接层输出的是一维向量logits=[1,2,3,4,5,6,7,8,9,10],这里假设总共类别数量为10，使用softmax分类器完成多类分类问题，并将损失函数设置为categorical_crossentropy损失函数：
首先用softmax将logits转换成一个概率分布，然后取概率值最大的作为样本的分类 。softmax的主要作用其实是在计算交叉熵上，将logits转换成一个概率分布后再来计算，然后取概率分布中最大的作为最终的分类结果，这就是将softmax激活函数应用于多分类中。

sigmoid激活函数应用于多标签分类–binary_crossentropy交叉熵损失函数

sigmoid激活函数：

binary_crossentropy交叉熵损失函数：

sigmoid一般不用来做多类分类，而是用来做二分类，它是将一个标量数字转换到[0,1]之间，如果大于一个概率阈值(一般是0.5)，则认为属于某个类别，否则不属于某个类别。这一属性使得其适合应用于多标签分类之中，在多标签分类中，大多使用binary_crossentropy损失函数。它是将一个标量数字转换到[0,1]之间，如果大于一个概率阈值(一般是0.5)，则认为属于某个类别。本质上其实就是针对logits中每个分类计算的结果分别作用一个sigmoid分类器，分别判定样本是否属于某个类别同样假设，神经网络模型最后的输出是这样一个向量logits=[1,2,3,4,5,6,7,8,9,10], 就是神经网络最终的全连接的输出。这里假设总共有10个分类。
sigmoid应该会将logits中每个数字都变成[0,1]之间的概率值，假设结果为[0.01, 0.05, 0.4, 0.6, 0.3, 0.1, 0.5, 0.4, 0.06, 0.8], 然后设置一个概率阈值，比如0.3，如果概率值大于0.3，则判定类别符合，那么该输入样本则会被判定为类别3、类别4、类别5、类别7及类别8。即一个样本具有多个标签。

详情请参考：

https://blog.csdn.net/uncle_ll/article/details/82778750

https://blog.csdn.net/koreyoshichen/article/details/84823636

darknet-yolov3 loss函数

源码中loss函数的实现形式：

1.先计算各个维度的delta值；

2.计算各个维度的delta的平方和。

1.在目标检测任务里，有几个关键信息是需要确定的: (x,y),(w,h),class,confidence。

delta(x,y,w,h)如下代码：

float delta_yolo_box(box truth, float *x, float *biases, int n, int index, int i, int j, int lw, int lh, int w, int h, float *delta, float scale, int stride)
{
    box pred = get_yolo_box(x, biases, n, index, i, j, lw, lh, w, h, stride);
    float iou = box_iou(pred, truth);

    float tx = (truth.x*lw - i);
    float ty = (truth.y*lh - j);
    float tw = log(truth.w*w / biases[2*n]);
    float th = log(truth.h*h / biases[2*n + 1]);

    delta[index + 0*stride] = scale * (tx - x[index + 0*stride]);
    delta[index + 1*stride] = scale * (ty - x[index + 1*stride]);
    delta[index + 2*stride] = scale * (tw - x[index + 2*stride]);
    delta[index + 3*stride] = scale * (th - x[index + 3*stride]);
    return iou;
}

注解：

x，y，w，h采用的是MSE均方误差损失函数。

delta（class）如下代码：

void delta_yolo_class(float *output, float *delta, int index, int class, int classes, int stride, float *avg_cat)
{
    int n;
    if (delta[index]){
        delta[index + stride*class] = 1 - output[index + stride*class];
        if(avg_cat) *avg_cat += output[index + stride*class];
        return;
    }
    for(n = 0; n < classes; ++n){
        delta[index + stride*n] = ((n == class)?1 : 0) - output[index + stride*n];
        if(n == class && avg_cat) *avg_cat += output[index + stride*n];
    }
}

注解：

论文如下：

1.但是源代码中还是应用的MSE损失函数？？？？

有一种解释：对于Logistic回归，正好方差损失和交叉熵损失的求导形式是一样的，作者这里直接用方差损失代替了，因为数值趋势上是一样的。可参考（https://blog.csdn.net/jasonzzj/article/details/52017438）

2.delta[index]是否为0的判断？？？？

因为选用的为sigmod-loss损失函数，具体请参考：

https://blog.csdn.net/jiyangsb/article/details/81976090

delta（confidence）如下代码：

for (b = 0; b < l.batch; ++b) {
        for (j = 0; j < l.h; ++j) {
            for (i = 0; i < l.w; ++i) {
                for (n = 0; n < l.n; ++n) {
                    ...
                    //负样本目标confidence
                    int obj_index = entry_index(l, b, n*l.w*l.h + j*l.w + i, 4);
                    avg_anyobj += l.output[obj_index];
                    l.delta[obj_index] = 0 - l.output[obj_index];
                    if (best_iou > l.ignore_thresh) {
                        l.delta[obj_index] = 0;
                    }
                    if (best_iou > l.truth_thresh) {
                        l.delta[obj_index] = 1 - l.output[obj_index];

                       ...
                    }
                }
            }
        }
        for(t = 0; t < l.max_boxes; ++t){
           ...
			
            int mask_n = int_index(l.mask, best_n, l.n);
            if(mask_n >= 0){
               ...
				//正样本目标confidence
                int obj_index = entry_index(l, b, mask_n*l.w*l.h + j*l.w + i, 4);
                avg_obj += l.output[obj_index];
                l.delta[obj_index] = 1 - l.output[obj_index];

               ...
            }
        }
    }

注解：

ignore_thresh：当框的iou大于忽略阈值时，此框不在参与负样本的loss计算， l.delta[obj_index] = 0。

可以看出，此处也为Mse损失函数。

2.计算均方差：

*(l.cost) = pow(mag_array(l.delta, l.outputs * l.batch), 2);

注解：

float mag_array(float *a, int n)
{
    int i;
    float sum = 0;
    for(i = 0; i < n; ++i){
        sum += a[i]*a[i];   
    }
    return sqrt(sum);
}

Keras-yolov3 loss函数

损失函数如下所示：

xy_loss = object_mask * box_loss_scale * K.binary_crossentropy(raw_true_xy, raw_pred[..., 0:2],from_logits=True)
wh_loss = object_mask * box_loss_scale * 0.5 * K.square(raw_true_wh - raw_pred[..., 2:4])
confidence_loss = object_mask * K.binary_crossentropy(object_mask, raw_pred[..., 4:5], from_logits=True) + (1 - object_mask) * K.binary_crossentropy(object_mask, raw_pred[..., 4:5],from_logits=True) * ignore_mask
class_loss = object_mask * K.binary_crossentropy(true_class_probs, raw_pred[..., 5:], from_logits=True) 
xy_loss = K.sum(xy_loss) / mf
wh_loss = K.sum(wh_loss) / mf
confidence_loss = K.sum(confidence_loss) / mf
class_loss = K.sum(class_loss) / mf
loss += xy_loss + wh_loss + confidence_loss + class_loss

注解：

binary_crossentropy：二进制交叉熵损失函数；

square：均方差损失函数。

损失函数：
xy_loss：中心点的损失值。object_mask是y_true的第4位，即是否含有物体，含有是1，不含是0。box_loss_scale的值，与物体框的大小有关，2减去相对面积，值得范围是(1~2)。binary_crossentropy是二值交叉熵。
wh_loss：宽高的损失值。除此之外，额外乘以系数0.5，平方K.square()。
confidence_loss：框的损失值。两部分组成，第1部分是存在物体的损失值，第2部分是不存在物体的损失值，其中乘以忽略掩码ignore_mask，忽略预测框中IoU小于阈值的框。
class_loss：类别损失值。
将各部分损失值的和，除以均值，累加，作为最终的图片损失值。

详情请参考：https://blog.csdn.net/weixin_33725722/article/details/87985552

Pytorch-yolov3 loss函数

损失函数如下所示：

    #顾名思义这里的x，y，z，w都是采用的最小均方差来评判误差
    #位置损失
    loss_x = self.mse_loss(x[obj_mask], tx[obj_mask])
    loss_y = self.mse_loss(y[obj_mask], ty[obj_mask])
    loss_w = self.mse_loss(w[obj_mask], tw[obj_mask])
    loss_h = self.mse_loss(h[obj_mask], th[obj_mask])

    #置信度损失，即有没有这个物体的概率
    #bce_loss：二进制交叉熵
    loss_conf_obj = self.bce_loss(pred_conf[obj_mask], tconf[obj_mask])
    loss_conf_noobj = self.bce_loss(pred_conf[noobj_mask], tconf[noobj_mask])
    loss_conf = self.obj_scale * loss_conf_obj + self.noobj_scale * loss_conf_noobj

    #分类的损失 二分类交叉熵，bce_loss其实是个迭代器计算所有的误差然后求和。
    loss_cls = self.bce_loss(pred_cls[obj_mask], tcls[obj_mask])
    #all
    total_loss = loss_x + loss_y + loss_w + loss_h + loss_conf + loss_cls

Giou-loss函数

1.简介：

论文：《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》

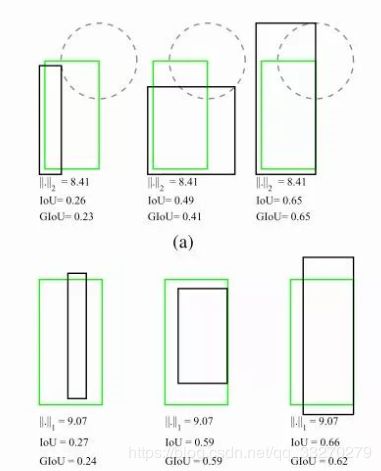
IoU是检测任务中最常用的指标，由于IoU是比值的概念，对目标物体的scale是不敏感的。然而检测任务中的BBox的回归损失(MSE loss, l1-smooth loss等）优化和IoU优化不是完全等价的（见下图）。

而且 Ln 范数对物体的scale也比较敏感。这篇论文提出可以直接把IoU设为回归的loss。然而有个问题是IoU无法直接优化没有重叠的部分。为了解决这个问题这篇paper提出了GIoU的思想。

假如现在有两个任意性质 A，B，我们找到一个最小的封闭形状C，让C可以把A，B包含在内，然后我们计算C中没有覆盖A和B的面积占C总面积的比值，然后用A与B的IoU减去这个比值：

损失函数：

2.在darknet中实现：

开源项目：https://github.com/generalized-iou/g-darknet

工程优化：

1.工程变动：

cfg文件：

loss函数的类型可以通过文件中的iou_loss选项进行选择，在.cfg中的每[yolo]一层上指定。当前的有效选项是：[iou|giou|mse]

iou_loss=mse		#原始darknet loss函数类型（全部mse）
iou_loss=iou		#x,y,w,h由mse损失函数换位box的iou-loss，confidence和class用mse。
iou_loss=giou		#x,y,w,h由mse损失函数换位box的giou-loss，confidence和class用mse。

新增不同维度loss函数的权重参数，表征其在总loss的重要程度，在.cfg中的每[yolo]一层上指定。具体如下：

cls_normalizer=1		#class和confidence的权重参数，默认值1
iou_normalizer=0.5		#box-iou的权重参数，默认值1。
						#通过验证，以上参数的初始化为最优。

data文件：

classes= 22
train  = ../train.txt
valid  = ../valid.txt
names = data/xxx.names
backup = backup
prefix = giou #新增输出前缀参数。

数据增强：

用AlexeyAB’s fork中的OpenCV实现的方式替换了原darknet中的数据加载和增强的方式。

数据增强函数在g-darknet\src\image_opencv.cpp中的image image_data_augmentation()。

注：其余操作与原darknet一致，请参考《yolov3的环境搭建与应用》，该工程剩余新增功能暂不做尝试

2.试验对比：

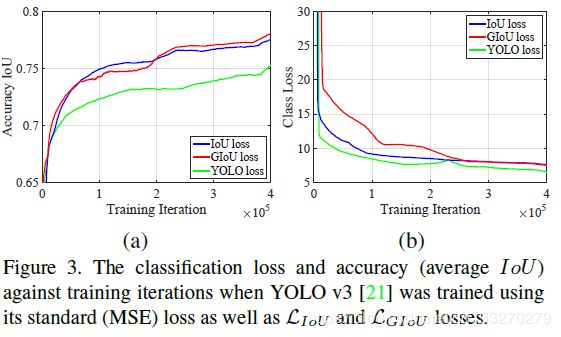
论文结果：

使用LGIoU损失时，YOLO v3的定位精度会大大提高（图3（a））。 然而，class不是最佳的（图3（b））。 由于AP受定位精度影响较小，受分类性能影响较大，所以修改cls_normalizer、iou_normalizer，对检测效果的影响较大。

实验结果：

1.Giou的Map低于Mse。

2.Giou的定位精度稍好于Mse。
原因如figure3注解。