字符串匹配原理及实现(C++版)
字符串匹配原理及实现(C++版)
- 1. 字符串匹配概念
- 2. BF
- 2.1 原理
- 2.2 代码实现
- 3. KMP
- 3.1 原理
- 3.2 代码实现
- 4. BM
- 4.1 坏字符
- 4.2 好后缀
- 4.3 代码实现
1. 字符串匹配概念
在查找操作中,我们用到很重要的概念就是字符串匹配,所谓字符串匹配就是在文本串中搜索模式串是否存在及其存在的位置。下面介绍几种字符串匹配的方法。
2. BF
2.1 原理
BF(暴力法)是一种最简单的字符串匹配算法,匹配过程如下:

文本串中的 I 和模式串中的 II 实现了匹配。
如果 I 和 II 下一个都是 A ,那么匹配长度增长,I 变成 III ,II 变成 IV 。
如果 III 的下一个是 A ,IV 的下一个是 B ,那么匹配失败,模式串向后移动一个字符,重新开始字符串匹配。
BF 的特点:
1.模式串与文本串的匹配是自左向右的进行。
2.一旦模式串与文本串失配,模式串只能向右移动一个字符。
2.2 代码实现
/*
* 暴力法:用于字符串匹配
* string t:文本串
* string p:模式串
* 返回值:返回首次匹配(完全匹配)位置(失败返回-1)
*/
int BruteForce(string t, string p){
int lenT = t.size();
int lenP = p.size();
int i, j;
for (i = 0; i <= lenT - lenP; ++i){
for (j = 0; j < lenP; ++j){
if (t[i + j] != p[j]){
break;
}
}
if (j == lenP){
return i;
}
}
return -1;
}
3. KMP
3.1 原理
可以看出,BF 中的匹配过程如下:
1.单次:多次成功,一次失败。
2.总体:多次失败,一次成功。
因为每次比对,都经历了多次成功,而经历了一次失败,然后需要模式串移动一个字符。显然,这种方法没有吸取 先前匹配成功的经验,实际上我们可以通过这种经验改进匹配过程。KMP 就是一种改进版的字符串匹配方法,匹配过程如下:

我们考虑在第一个文本串和模式串对齐方式中,I 和 II 是匹配的,那么,模式串能够从第一个对齐位置移动到下一个对齐位置的条件是 III 和 IV 是匹配的。
由此我们可以总结:
1.移动对齐方式只由文本串与模式串失配位置决定。
2.而与文本串与模式串失配位置的文本串字符无关。
3.也就是说,移动对齐方式只与模式串有关。
那么,我们完全可以根据模式串预先算出一张表,由此得到在不同的位置上失配可以移动模式串的字符距离。
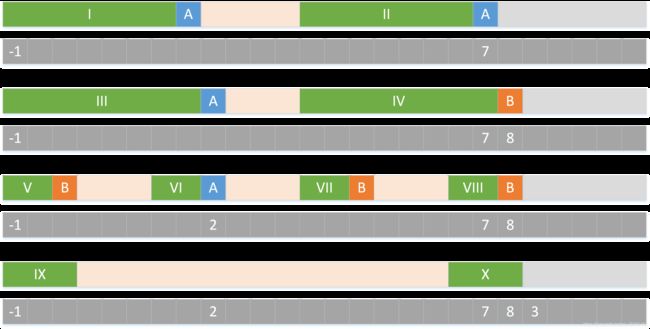
在第一个对齐方式中,I 和 II 是匹配的,匹配长度是 7 个字符,那么我们可以在表中记录数字 7,即该表存储的是当前字符前面的字符串 头 和 尾 匹配的长度。
推导表格的方法我们采用递推的方法,假设已经有了第一个对齐位置的匹配,即 I 和 II 是匹配的,匹配长度是 7。
如果 I 和 II 的下一个字符都是 A,那么 I 变成 III ,II 变成 IV,即匹配长度 + 1,在表中记录数字 8。
如果 III 的下一个字符是 A ,IV 的下一个字符是 B,那么问题就不再那么简单了。
首先,细分 III 字符串,可以看到 V 和 VI 是匹配的,同理,VII 和 VIII 是匹配的。此时刚好 V 的下一个字符是 B,那么就实现了匹配, V 变成 IX,VIII 变成 X。在表格中记录数字 3。
如果 V 的下一个字符依旧不是 B,我们就可以将 V 继续细分,方法与上类似。如果细分到最后还是找不到字符 B,那么就只能将模式串移动一个字符,即只能在表中记录数字 0,表示当前字符前面的字符串 头 和 尾 匹配的长度是 0。
创建 next 表的代码如下:
/*
* 创建next表
* string p:模式串
* int next[]:next表
*/
void CreatNext(string p, int next[]){
int lenP = p.size();
int i = 0, j = -1;
next[0] = -1;
while (i < lenP - 1){
if (j < 0 || p[i] == p[j]){
i++;
j++;
next[i] = j; //此句代码还可以改进
}
else{
j = next[j];
}
}
}
其实,next 表的创建方法还可以改进。

首先 I 和 II 是匹配的,III 和 IV 是匹配的,按第一种创建方式, II 和 IV 的下一个字符对应的表格都应该记录数字 3。但是实际上,如果 IV 的下一个字符发生了失配,而 IV 和 III 的下一个字符都是 A 的话,即使将 III 移动到 IV 的位置上,结局依然是失配,而我们可以通过改进 next 表的创建方式来避免这种不必要的操作。
/*
* 创建next表改进版
* string p:模式串
* int next[]:next表
*/
void CreatNext_E(string p, int next[]){
int lenP = p.size();
int i = 0, j = -1;
next[0] = -1;
while (i < lenP - 1){
if (j < 0 || p[i] == p[j]){
i++;
j++;
next[i] = p[i] == p[j] ? next[j] : j; //此句代码进行了改进
}
else{
j = next[j];
}
}
}
KMP 的特点:
1.模式串与文本串的匹配是自左向右的进行。
2.一旦模式串与文本串失配,模式串依靠 next 表向右移动若干个字符。
3.2 代码实现
next 表的创建代码不再赘述。
/*
* KMP法:用于字符串匹配
* string t:文本串
* string p:模式串
* 返回值:返回首次匹配(完全匹配)位置(失败返回-1)
*/
int KnuthMorrisPratt(string t, string p){
int lenT = t.size();
int lenP = p.size();
int *next = new int[lenP];
//CreatNext(p, next);
CreatNext_E(p, next);
int i, j;
for (i = 0; i <= lenT - lenP; ){
for (j = 0; j < lenP; ++j){
if (t[i + j] != p[j]){
i += j - next[j];
break;
}
}
if (j == lenP){
return i;
}
}
return -1;
}
4. BM
4.1 坏字符
在 BF 算法中,总结起来就是:
1.单次:多次成功,一次失败。
2.总体:多次失败,一次成功。
可以看出来,除了成功匹配的那次对比,其余的各次都是因为一次失配引起的。但是,在一般情况下,失败的概率与成功的概率相比,简直是微乎其微。所以,与其说是寻找匹配,不如说是加速失败。这里的坏字符说的就是加速失败。
在 坏字符 策略中,有这样的情况,这里 I 和 II 已经成功匹配。而 I 前面的一个字符是 A,II 的前面一个字符是 B,发生了失配。那么,接下来,我们在模式串中找到字符 A,然后将两者相应对齐。那么,会有以下几种情况:
1.A(一个或多个)在 B 的前面:那么这时我们为了 加速匹配 进程而又 避免遗漏,可以把(最右边的 A)移动到文本串的 A 位置,与之对齐。

2.A(无或有)在 B 的后面:如果模式串中没有字符 A,那么直接将模式串向右移动一个字符。而如果 A 在 B 的后面,那么就不能把 A 和文本串的 A 对齐,因为这样会引起字符串匹配的回溯,是没有意义的。这时依旧是将模式串向右移动一个字符。

因为我们需要知道的是某个字符在模式串中的有无以及最右边的位置,所以我们可以构建一个 bc 表,用来记录这些信息,方便我们查找。显然,bc 表要能够涵盖整个文本串与模式串中包含的字符集合。
下面给出 bc 表的演示(没有的记作 - 1):

下面给出实现代码:
/*
* 创建bc表
* string p:模式串
* int bc[]:bc表
*/
void CreatBc(string p, int bc[]){
int lenP = p.size();
int i;
for (i = 0; i < 256; bc[i++] = -1);
for (i = 0; i < lenP; ++i){
bc[p[i]] = i;
}
}
BC 的特点:
1.模式串与文本串的匹配是自右向左的进行。
2.一旦模式串与文本串失配,模式串依靠 bc 表向右移动若干个字符。
4.2 好后缀
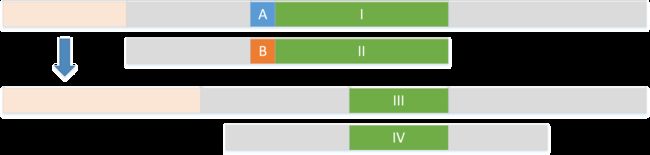
这里 I 和 II 以及成功匹配,A 和 B 发生失配,那么这时模式串移动到下一位置的条件就是 III 和 IV 是匹配的。

让我们把视野放到模式串上,如果 I 和 II 匹配,当 II 前面一个字符发生失配,那么模式串对应需要向右移动 12 个字符。然后在 gs 表中记录数字 12。

但是,直接得到 gs 表十分困难,我们需要一个 ss 表作为中间转换。这里的 7 表示 I 和 II 的匹配长度是 7。ss 表的创建过程如下:

首先,I 和 II 已经匹配,匹配长度为3。
1.此时,I 和 II 前面一个字符都是 A,那么匹配长度 + 1 变成 4。
2.III 的前面一个字符是 A,IV 的前面一个字符是 B,发生了失配。所以在 ss 表中记录数字 4。
3.将 hi 指到当前位置,因为之前已经匹配过了,所以不需要重复匹配,直接把 1 记录在ss 表中。
4.将 hi 指到当前位置,虽然这里之前匹配过了,但是 VIII 中记录的是 3,但是这段长度为 3 的字符串中的 B 和前面的 A 已经失配,所以不能直接记录 3,而是要重新比较。
具体实现代码如下:
/*
* 创建ss表
* string p:模式串
* int ss[]:ss表
*/
void CreatSs(string p, int ss[]){
int lenP = p.size();
int i, hi, lo;
ss[lenP - 1] = lenP;
for (hi = lo = lenP - 1, i = lo - 1;i >= 0; --i){
if (i > lo && ss[lenP - 1 - hi + i] <= i - lo){
ss[i] = ss[lenP - 1 - hi + i];
}
else{
hi = i;
lo = __min(hi, lo);
while (lo >= 0 && p[lo] == p[lenP - 1 - hi + lo]){
lo--;
}
ss[i] = hi - lo;
}
}
}
那么,接下来讨论从 ss 表到 gs 表的变换。下图中第一行是模式串,第二行是 ss 表,第三行是 gs 表。
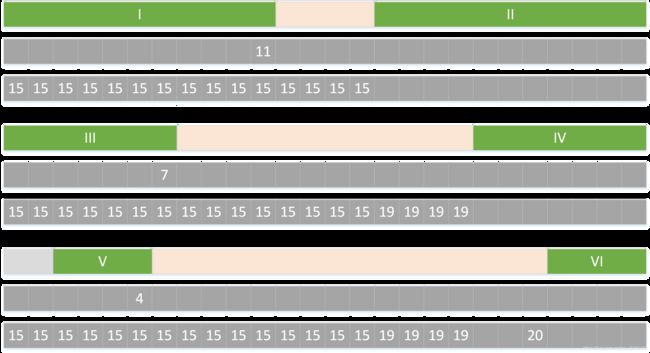
1.如果匹配方式是 I 和 II 匹配,那么 II 前面的字符串中的每个字符发生失配都可能会移动 15 个字符。
2.III 和 IV 匹配成功,IV 前面字符串的每个字符发生失配都可能移动 19 个字符。
3.V 和 VI 匹配成功,VI 前面的那个字符发生失配可能需要移动 20 个字符。
注:这里是可能并不是一定,实际移动距离取所有可能的最小值。(为了避免遗漏)
/*
* 创建gs表
* string p:模式串
* int gs[]:gs表
*/
void CreatGs(string p, int gs[]){
int lenP = p.size();
int *ss = new int[lenP];
CreatSs(p, ss);
int i, j;
for (i = 0; i < lenP; ++i){
gs[i] = lenP;
}
for (i = 0, j = lenP - 1; j >= 0; --j){
if (ss[j] == j + 1){
while (i < lenP - 1 - j){
gs[i++] = lenP - 1 - j;
}
}
}
for (i = 0; i < lenP - 1; ++i){
gs[lenP - 1 - ss[i]] = lenP - 1 - i;
}
delete[] ss;
}
GS 的特点:
1.模式串与文本串的匹配是自右向左的进行。
2.一旦模式串与文本串失配,模式串依靠 gs 表向右移动若干个字符。
所谓 BM,就是综合了 BC 和 GS 两个策略进行的字符串匹配算法。
BM 的特点:
1.模式串与文本串的匹配是自右向左的进行。
2.一旦模式串与文本串失配,模式串依靠 bc 表和 gs 表向右移动若干个字符。(取 bc 表和 gs 表的较大值)
4.3 代码实现
/*
* BM法:用于字符串匹配
* string t:文本串
* string p:模式串
* 返回值:返回首次匹配(完全匹配)位置(失败返回-1)
*/
int BoyerMoore(string t, string p){
int lenT = t.size();
int lenP = p.size();
int *bc = new int[256];
CreatBc(p, bc);
int i, j;
/*for (i = 0; i <= lenT - lenP;){
for (j = lenP - 1; j >= 0; --j){
if (t[i + j] != p[j]){
i += (j - bc[t[i + j]] > 0) ? j - bc[t[i + j]] : 1;
break;
}
}
if (j == -1){
return i;
}
}*/
int *gs = new int[lenP];
CreatGs(p, gs);
for (i = 0; i <= lenT - lenP;){
for (j = lenP - 1; j >= 0; --j){
if (t[i + j] != p[j]){
int max = __max(j - bc[t[i + j]], gs[j]);
i += max;
break;
}
}
if (j < 0){
return i;
}
}
return -1;
}