排序算法之mergeSort,quikSort,heapSort
排序算法之归并排序,快速排序,堆排序
- 温习
- 归并排序
- 数组的归并排序
- 单链表的归并排序
- 快速排序
- 堆排序
- 标准库自带的排序sort
- 头文件
- sort定义
- 使用示例
温习
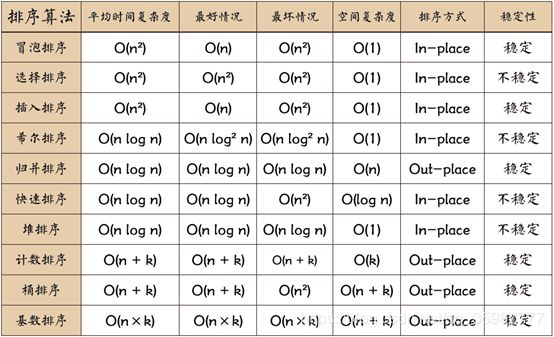
关于稳定性
- 稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序。
- 不是稳定的排序算法:选择排序(示例【2 3 2 1】)、快速排序(示例【3 1 2 3 5 4】主元2)、希尔排序(示例【1 5 5 2 4】希尔序列)、堆排序(示例【3 2 3 2】最小堆)。
归并排序
归并排序假设所有数据分成两组,每组都是已经排序好的。
每次从两组数据中找出各自最小的并选择更小的那个转移到另外一个新数组中(额外空间),当所有数据都转移完成后排序结束。把新数组中所有数字按顺序转移回原数组。
在进行归并之前先针对两组数字递归调用归并排序函数。
数组的归并排序
#define _CRT_SECURE_NO_WARNINGS
#include单链表的归并排序
//1.3单链表归并排序
//先用快慢指针找到链表中点,
//然后左边递归,右边递归,最后merge两个有序链表
ListNode* merge(ListNode* left,ListNode* right);
ListNode* listMergeSort(ListNode* head){
if(!head||!head->next)
return head;
ListNode* fast=head;
ListNode* slow=head;
//1.先用快慢指针找到链表中点,
//如果结点个数是奇数,slow指向中间那个,fast最后指向最后一个结点
//如果结点个数是偶数,slow指向中间两个元素的右边那个,fast是nullptr
//发现这里会导致链表只有两个结点时,无限递归的问题,可以举例想想为啥?
// while(fast&&fast->next){
// fast=fast->next->next;
// slow=slow->next;
// }
//所以这里,如果结点个数是偶数,必须让slow指向左中值位置,可以举例想想为啥?
//如果结点个数是奇数,slow指向中间那个,fast最后指向最后一个结点
//如果结点个数是偶数,slow指向中间两个元素的左边那个,fast指向倒数第二个
while(fast->next&&fast->next->next){
fast=fast->next->next;
slow=slow->next;
}
//2.然后左边递归,右边递归,最后merge两个有序链表
ListNode* temp=slow->next;
slow->next=nullptr;//构造子链表尾,
ListNode* left=listMergeSort(head);
ListNode* right=listMergeSort(temp);
return merge(left,right);
}
ListNode* merge(ListNode* left,ListNode* right){
ListNode* head=nullptr;
ListNode* tail=nullptr;
//左右都没到尾部
while(left&&right){
if(left->value < right->value){
if(head==nullptr){
head=left;
tail=left;
left=left->next;
}else{
tail->next=left;
tail=left;
left=left->next;
}
}else{
if(head==nullptr){
head=right;
tail=right;
right=right->next;
}else{
tail->next=right;
tail=right;
right=right->next;
}
}
}
//有一方先到尾部
//left到尾部了
if(left==nullptr)
tail->next=right;
//right到尾部了
if(right==nullptr)
tail->next=left;
return head;
}
//测试排序结果
int main(){
vector<ListNode> myVector{ListNode(5),ListNode(2),ListNode(6),ListNode(0),ListNode(1)};
//ptr指向myVector中开始位置的元素
vector<ListNode>::pointer head=myVector.data();//即&myVector[0]
//构造链表
for(int i=0;i<myVector.size()-1;i++){
myVector[i].next=&myVector[i+1];
}
myVector.back().next=nullptr;
head=listMergeSort(head);
cout<<"after sorted: ";
ListNode* cur=head;
while(cur!=nullptr){
cout<<cur->value<<" ";
cur=cur->next;
}
system("pause");
return 0;
}
补充一下快慢指针返回单链表中点的几种情况
ListNode* fast = head;
while (fast->next != nullptr && fast->next->next != nullptr) {
slow = slow->next;
fast = fast->next->next;
}
这种情况slow是中点,链表长度为偶数时为左边元素。
链表长度为偶数时fast为倒数第二个元素,奇数时为最后一个元素。
ListNode* fast = head;
while (fast != nullptr && fast->next != nullptr) {
slow = slow->next;
fast = fast->next->next;
}
这种情况slow是中点,链表长度为偶数时为右边元素。
链表长度为偶数时fast为null,奇数时为最后一个元素。
ListNode* fast = head->next;
while (fast != nullptr && fast->next != nullptr) {
slow = slow->next;
fast = fast->next->next;
}
这种情况slow是中点,链表长度为偶数时为左边元素。
链表长度为偶数和奇数时fast均为最后一个元素。
快速排序
实现快速排序算法的关键在于先在数组中选择一个数字作为主元pivot,接下来把数组中的数字分为两部分,比选择的数字小的移到数组的左边,比选择的数字大的移到数组的右边
- 随机快速排序步骤
- 随意选择主元,然后将主元交换到数组尾部
- 划分,将小于主元的放置在最左边(little区域向右生长),大于主元的放置在最右边(more区域向左生长),等于主元的放中间
- 递归
//C语言int占4个字节,一共32位,范围是-2147483648 ~ 2147483647。
#ifndef QUICKSORT_H
#define QUICKSORT_H
#include堆排序
时间复杂度O(N*logN),额外空间复杂度O(1)。
给定一个数组,原地建大顶堆,同时对数组原地堆排序,
这里堆是从下标0开始的,关于堆从下标0还是下标1开始,都可以,
- 从0开始,i结点的左孩子2i+1,右孩子2i+2, index结点的父亲:(index-1)/2;
- 从1开始,i结点的左孩子2i,右孩子2i+1, index结点的父亲:index)/2;
堆排序的细节和复杂度分析
时间复杂度O(N*logN),额外空间复杂度O(1)
1,堆结构的heapInsert与heapify
2,堆结构的增大和减少
3,如果只是建立堆的过程,时间复杂度为O(N)
4,优先级队列结构,就是堆结构
//建最大堆过程: 遍历数组,每次与自己父节点比较,大于父节点就与父节点交换,一直上浮到根节点为止
//提示:下标i节点的父节点下标(i-1)/2;
//下标为i的节点的左孩子为(2*i+1),右孩子为2*i+2;
//函数含义:将数组arr中下标index的元素上浮到正确位置。
void heapInsert(int arr[], int index)
{
while (arr[index] > arr[(index - 1 )/ 2]) {
swap(arr[index], arr[(index - 1) / 2]);
index = (index - 1) / 2;
}
}
//函数含义:将数组arr中下标为index处的元素下潜到正确位置
void heapify(int arr[], int index, int heapSize)
{
int left = index * 2 + 1;
while (left < heapSize) {
int largest = left + 1 < heapSize && arr[left + 1] > arr[left]
? left + 1
: left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
//某个孩子比较大,那个孩子的位置是largest
swap(arr[largest], arr[index]);
index = largest;//下潜到较大孩子节点
left = index * 2 + 1;//准备下次循环
}
}
- 对数组原地堆排序,额外空间复杂度O(1),时间复杂度O(n*logn)
- 先利用heapInsert原地建立大顶堆,根节点即为max
- 然后将根节点(max)与最后一个元素交换,同时将堆的尾部前移(因为第一次的max已经放到正确位置了),
- 然后比较新的根节点与左右孩子节点中的最大值,新根节点小于左右节点最大值,则交换;若交换发生,就一直下潜到最下层;(这个方法用于删除头节点也可以)
一个数组int arr[]不是作为形参的话,sizeof(arr) / sizeof(*arr)就返回数组大小。
一个数组若作为形参的话,因为数组本身不能复制,形参只是一个指针,所以无法在函数里面通过上面的方式计算数组大小,所以一般得传入一个形参arrSize表示数组大小
void heapSort(int arr[],int arrSize)
{
if (arrSize< 2)
return;
for (int i = 0; i < arrSize; i++) {
heapInsert(arr, i);//原地建立大顶堆
}
int heapSize = arrSize;
swap(arr[0], arr[--heapSize]);//首次max,换到数组尾部
while (heapSize > 0) {
heapify(arr, 0, heapSize);//在数组arr的前heapSize个元素中,将下标0处元素下潜
swap(arr[0], arr[--heapSize]);//下潜完毕,将头部元素换到下标--heapSize处
}
}
- 完整测试代码:
#include标准库自带的排序sort
转载过一篇STL中排序函数Qsort,Sort,Stable_sort,Partial_sort,List::sort的用法
介绍了标准库自带的排序函数基本用法
参考:http://www.cplusplus.com/reference/algorithm/sort/?kw=sort
头文件
#includesort定义
template <class RandomAccessIterator>
void sort (RandomAccessIterator first, RandomAccessIterator last);
template <class RandomAccessIterator, class Compare>
void sort (RandomAccessIterator first, RandomAccessIterator last, Compare comp);
使用示例
// sort algorithm example
#include 标准库中还提供了如下的函数对象less、greater
std::less
template <class T> struct less {
bool operator() (const T& x, const T& y) const {return x<y;}
typedef T first_argument_type;
typedef T second_argument_type;
typedef bool result_type;
};
template <class T> struct greater {
bool operator() (const T& x, const T& y) const {return x>y;}
typedef T first_argument_type;
typedef T second_argument_type;
typedef bool result_type;
};
// less example
#include