二叉搜索树中的最近公共祖先

在一棵树T中两个结点u和v的最近公共祖先(LCA)，是树中以u和v为其后代的深度最大的那个结点。现给定某二叉搜索树(BST)中任意两个结点，要求你找出它们的最近公共祖先。

函数接口定义：

int LCA( Tree T, int u, int v );

其中Tree的定义如下：

typedef struct TreeNode *Tree;
struct TreeNode {
    int   Key;
    Tree  Left;
    Tree  Right;
};

函数LCA须返回树T中两个结点u和v的最近公共祖先结点的键值。若u或v不在树中，则应返回ERROR。

裁判测试程序样例：

#include 
#include 

#define ERROR -1
typedef struct TreeNode *Tree;
struct TreeNode {
    int   Key;
    Tree  Left;
    Tree  Right;
};

Tree BuildTree(); /* 细节在此不表 */
int LCA( Tree T,  int u, int v );

int main()
{
    Tree T;
    int u, v, ans;

    T = BuildTree();
    scanf("%d %d", &u, &v);
    ans = LCA(T, u, v);
    if ( ans == ERROR ) printf("Wrong input\n");
    else printf("LCA = %d\n", ans);

    return 0;
}

/* 你的代码将被嵌在这里 */

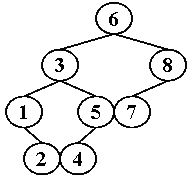
输入样例1 （对于下图给定的树）：

2 7

输出样例1：

LCA = 6

输入样例2 （对于例1中的树）：

1 9

输出样例2：

Wrong input

解题体会：起初看到这道题，就感觉没思路，就想搜题解。仔细一想，一直搜题解也不是办法，自主思考才能更快的提高能力。沉住气看了一会儿，问题就迎刃而解啦。
思路如下：
有两种情况：1.u,v不在树中；
                    2.u,v在树中：<1>u,v都在左子树上；
                                         <2>u,v都在右子树上；
                                         <3>u,v一个在左子树上，一个在右子树上；
                                         <4>u，v有一个在根上。 

题解代码：

int find(Tree T,int u)
{
    if(!T)
        return 0;
    if(T->Key==u)
        return 1;
    if(T->KeyRight,u);
    if(T->Key>u)
        return find(T->Left,u);
}

int LCA( Tree T,  int u, int v )
{
    if(!T)
        return ERROR;
    if(!find(T,u)||!find(T,v))
        return ERROR;
    if(u==T->Key||v==T->Key)
        return T->Key;
    if(u>T->Key&&vKey||uKey&&v>T->Key)
        return T->Key;
    if(u>T->Key)
        return LCA(T->Right,u,v);
    if(uKey)
        return LCA(T->Left,u,v);
}

解题过程中的所有代码：

#include 
#include 

#define ERROR -1
typedef struct TreeNode *Tree;
struct TreeNode {
    int   Key;
    Tree  Left;
    Tree  Right;
};

Tree insertTree(Tree T,int a);
Tree BuildTree();
int find(Tree T,int u);
int LCA( Tree T,  int u, int v );
void inOrder(Tree T);

int main()
{
    Tree T;
    int u, v, ans;

    T = BuildTree();
    inOrder(T);
    printf("\n");
    scanf("%d %d", &u, &v);
    ans = LCA(T, u, v);
    if ( ans == ERROR ) printf("Wrong input\n");
    else printf("LCA = %d\n", ans);

    return 0;
}

Tree insertTree(Tree T,int a)//插入结点
{
    if(!T)
    {
        T=(Tree)malloc(sizeof(struct TreeNode));
        T->Key=a;
        T->Left=T->Right=NULL;
    }else{
        if(aKey)
            T->Left=insertTree(T->Left,a);
        else
            T->Right=insertTree(T->Right,a);
    }
    return T;
}

Tree BuildTree()//采用插入结点进行建树
{
    Tree T=NULL;
    int n,a;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d",&a);
        T=insertTree(T,a);
    }
    return T;
}

int find(Tree T,int u)//查看u是否在树中
{
    if(!T)
        return 0;
    if(T->Key==u)
        return 1;
    if(T->KeyRight,u);
    if(T->Key>u)
        return find(T->Left,u);
}

int LCA( Tree T,  int u, int v )//寻找u,v的共同祖先
{
    if(!T)
        return ERROR;
    if(!find(T,u)||!find(T,v))
        return ERROR;
    if(u==T->Key||v==T->Key)
        return T->Key;
    if(u>T->Key&&vKey||uKey&&v>T->Key)
        return T->Key;
    if(u>T->Key)
        return LCA(T->Right,u,v);
    if(uKey)
        return LCA(T->Left,u,v);
}

void inOrder(Tree T)//中序输出二叉排序树，利用二叉排序树中序遍历序列递增来检验建树函数
{
    if(T)
    {
        inOrder(T->Left);
        printf(" %d",T->Key);
        inOrder(T->Right);
    }
}