Python信号处理：波束形成及目标方位估计，CBF、MVDR

摘要：一直以来都是用MATLAB做信号处理，得到预处理的特征后再用Python进一步应用神经网络之类的方法。这里利用Python实现了常规波束形成(CBF)、MVDR波束形成以及波束扫描方位估计。本文实现的都是窄带波束形成，一种简单的宽带波束形成方法时直接将不同频率的窄带输出相加，比较容易扩展。

系列目录

1. Python信号处理：快速傅里叶变换(FFT)，短时傅里叶变换(STFT)，窗函数，以及滤波
2. Python信号处理：自相关函数(对标MATLAB中的autocorr)
3. Python信号处理：波束形成及目标方位估计，CBF、MVDR
4. Python信号处理：cvxpy工具包求解稀疏约束优化问题

目录

1. 波束形成和方位估计
2. 常规波束形成器
3. MVDR波束形成器

1. 波束形成和方位估计

波束形成就是通过一个加权向量$w$对阵列接收到的数据$x$加权相加得到输出$y=w^{H}x$，所以确定$w$是波束形成中非常重要的步骤，知道$w$就知道了波束输出。波束形成器的设计问题其实就是设计加权向量$w$。

已知阵列的方向响应向量为$a(\theta )=[1,e^{-\mathrm{i}\frac{2\pi }{\lambda }\mathrm{d}\sin \theta },...,e^{-\mathrm{i}\frac{2\pi }{\lambda }(\mathrm{N}-1)\mathrm{d}\sin \theta }{]}^H$
，则波束响应为
$$B(\theta )=w^{H}a(\theta ).$$
波束响应只与加权向量和方向响应向量有关，而与是否存在信号无关。对于确定方向的加权向量$w$，改变方向响应向量就可以得到波束响应能量相对于不同方向的函数图，也就是波束图。波束图反映了波束形成器的空域滤波性能。

加权向量$w$是波束观察方向${\theta }_0$的函数，因此在波束观察方向的波束输出功率可以表示为
$${\sigma }_y^2({\theta }_0)=y({\theta }_0)y^H({\theta }_0)=w^H({\theta }_0)x{x}^{H}w({\theta }_0)=w({\theta }_0{)}^H{R}_{x}w({\theta }_0),$$
其中$R_x$是接收数据的协方差矩阵。改变波束观察方向${\theta }_0$，就可以获得在整个观察区内的波束输出功率，此时的到的就是波束扫描方位谱。

波束形成和方位估计，分别可以得到波束图和波束扫描方位谱，两者十分相似，在常规波束形成中，两者甚至在形式上一样的。但两者的意义差别很大。

• 波束图用于表示波束形成器的空域滤波性能，即给定波束形成器，看它对各方位信号的响应大小。计算波束图时，波束加权向量是固定的，通过扫描阵列的方向响应向量获得不同方向的波束响应。从波束图可以观察到各方位信号对感兴趣的方位(波束观察方向)波束输出的影响。波束图与是否存在信号无关。

• 方位谱用于估计各方位到达信号功率的大小。利用波束扫描法计算方位谱时，加权向量是观察方向的函数，方位谱的峰值所在可以用于估计信号的方位。

2. 常规波束形成器

常规波束形成器的原理是延时加权求和，加权向量正好就是阵列方向相应向量相位的变化，即$w=a({\theta }_0)$，因此波束响应为
$$B_{CBF}(\theta )=a^H({\theta }_0)a(\theta ),$$
其中，波束形成时的${\theta }_0$是不变的。

用于方位估计时，信号方位$\theta$时固定的，波束观察方向${\theta }_0$在观察区中变化，得到方位谱为
$$\begin{array}{rl}{\sigma }_y^2({\theta }_0)& =y({\theta }_0)y^H({\theta }_0)=w^H({\theta }_0)x{x}^{H}w({\theta }_0)\\ & ={\sigma }_s^2{w}^H({\theta }_0)a(\theta )a^H(\theta )w({\theta }_0)\end{array}$$

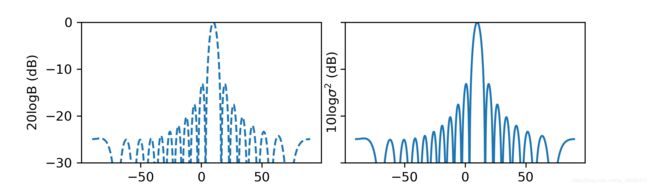
python实现如下，代码中变量命名和公式中相同，波束图和波束扫描方位谱如图所示。在白噪声背景下，CBF的两幅图是相同的。

import matplotlib.pyplot as plt
import numpy as np

d = np.array([15]) * np.ones([18, 1])
f = 50
lmbda = 1500 / f
N = 18
n = np.arange(0, N, 1).reshape([-1, 1])

# 波束形成
theta = np.arange(-90, 90, 0.1).reshape([1, -1])
theta_0 = 10
theta = theta / 180 * np.pi
theta_0 = theta_0 / 180 * np.pi

a = np.exp(1j * 2 * np.pi * np.sin(theta) * n * d / lmbda)
w = np.exp(1j * 2 * np.pi * np.sin(theta_0) * n * d / lmbda)
B = np.dot(a.transpose(), np.conj(w))
B = np.abs(B) / np.max(np.abs(B))

fig, ax = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(7, 2), dpi=300)
plt.subplots_adjust(wspace=0.1, hspace=0.05)

ax[0].plot(theta.reshape([-1,1])*180/np.pi, 20 * np.log10(B.reshape([-1,1])), '--')

# 方位估计
theta_0 = np.arange(-90, 90, 0.1).reshape([1, -1])
theta = 10
theta = theta / 180 * np.pi
theta_0 = theta_0 / 180 * np.pi

a = np.mat(np.exp(1j * 2 * np.pi * np.sin(theta) * n * d / lmbda))
w = np.mat(np.exp(1j * 2 * np.pi * np.sin(theta_0) * n * d / lmbda))

sigma = np.transpose(np.conj(w)) * a * np.transpose(np.conj(a)) * w
sigma = np.diag(sigma)
sigma = sigma / np.max(sigma)

ax[1].plot(theta_0.reshape([-1,1])*180/np.pi, 10 * np.log10(sigma))

3. MVDR波束形成器

最小方差无失真响应波束形成器，顾名思义有两个成分：1. 最小方差，2. 无失真，因此可以表示为
$$\underset{w}{\min }{w}^H{R}_{n}w,s.t.w^{H}a=1,$$
其中，优化目标表明为最小输出噪声方差，约束为无失真约束。实际中通常使用接收信号的协方差矩阵代替噪声协方差矩阵，此时方法也可以叫做最小功率无失真响应波束形成器(MPDR)，但叫MVDR也可以。

通过求解该约束优化问题，就可以得到波束形成器的加权向量，进而得到波束输出响应。有两种思路求解该优化问题：

1. 常规解法，通过lagrange乘子法，手动求解计算加权向量以及波束相应输出。
2. 工具包求解，利用一些优化工具包，直接求解该优化问题得到答案——这种方法实际上解决了大部分的波束形成问题，因为很多波束形成问题都是一个目标函数，再加上很多的约束，如果工具包能求解对应的优化问题，波束输出就有了。

这里直接给出第一种方法求出来的加权向量。第二种解法在后面内容中会详细介绍，作为一种通用的波束形成方法。因为都是优化问题，波束形成在算法上几乎没有什么难题，只有工程中的问题。

scipy.optimize.minimize失败了，因为只能处理实数的问题。MATLAB的CVX工具箱是能处理复数的，不知道cvxpy怎么样。。

cvxpy好像解不出复数最优解，目标函数里可以有复数操作，但最终的值必须是实数的，而且解出来的最优解也一直是实数，肯定哪里不太对。。

$$w_{MVDR}=\frac{R_x^{-1}a({\theta }_0)}{a^H({\theta }_0)R_x^{-1}a({\theta }_0)}$$
波束响应和波束输出功率，和第一部分的公式相同，即
$$B_{MVDR}=w^{H}a(\theta )$$
$${\sigma }_{MVDR}({\theta }_0)=w^H({\theta }_0)R_{x}w({\theta }_0)=\frac{1}{a^H({\theta }_0)R_x^{-1}a({\theta }_0)}$$

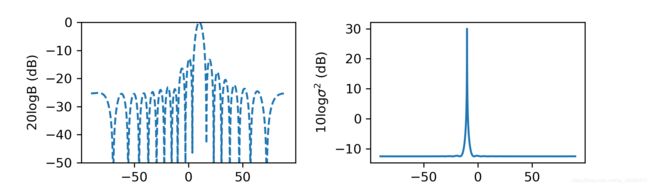
python实现如下，代码中变量命名和公式中相同，波束图和波束扫描方位谱如图所示。从波束图可以看出，当信号方向(-10°)和波束观察方向(10°)不同时，MVDR在信号方向会形成一个凹陷，降低了信号(此时信号算是干扰)的能量。

import matplotlib.pyplot as plt
import numpy as np

d = np.array([15]) * np.ones([18, 1])
f = 50
lmbda = 1500 / f
N = 18
n = np.arange(0, N, 1).reshape([-1, 1])

# 信号
theta = -10
theta = theta / 180 * np.pi
x = np.exp(1j * 2 * np.pi * np.sin(theta) * n * d / lmbda)
Rx = np.mat(1000 * np.dot(x, np.transpose(np.conj(x))) + 1 * np.eye(N))

# # 波束形成
theta = np.arange(-90, 90, 0.1).reshape([1, -1])
theta_0 = 10
theta = theta / 180 * np.pi
theta_0 = theta_0 / 180 * np.pi

a = np.mat(np.exp(1j * 2 * np.pi * np.sin(theta) * n * d / lmbda))

a_theta_0 = np.mat(np.exp(1j * 2 * np.pi * np.sin(theta_0) * n * d / lmbda))
w = Rx.I * a_theta_0 / (a_theta_0.H * Rx.I * a_theta_0)

B = w.H * a
B = np.abs(B) / np.max(np.abs(B))

fig, ax = plt.subplots(1, 2, sharex=True, sharey=False, figsize=(7, 2), dpi=300)
plt.subplots_adjust(wspace=0.35, hspace=0.05)

ax[0].plot(theta.reshape([-1,1])*180/np.pi, 20 * np.log10(B.reshape([-1,1])), '--')

# 方位估计
theta_0 = np.arange(-90, 90, 0.1).reshape([1, -1])
theta_0 = theta_0 / 180 * np.pi

sigma = []
for i in range(theta_0.shape[1]):
    a_theta_0 = np.mat(np.exp(1j * 2 * np.pi * np.sin(theta_0[:, i]) * n * d / lmbda))
    sigma.append((1 / (a_theta_0.H * Rx.I * a_theta_0)))
    
sigma = np.array(sigma).reshape([-1, 1])

ax[1].plot(theta_0.reshape([-1,1])*180/np.pi, 10 * np.log10(sigma))