Kaggle之泰坦尼克号
本文大部分内容参考于这里以及这里,主要用于自己阅读后的总结以及结果的复现。
由于在分析数据时大量利用pandas以及matplotlib进行可视化,因此参考这里进行了简单的入门学习,代码放在了这里
Titanic 是kaggle上每个新手都要接触的第一个项目。机器学习在最开始创建模型的时候不要先想着做得完美,可以先做一个baseline出来,再慢慢挖掘数据的特征优化模型。
前人说过,对数据的特征分析比模型的建立还重要,因此打算用Titanic这个数据集,对特征分析(feature engineering) 作一个深入的了解。
数据分析
首先在拿到Titanic模型的train.csv和test.csv后,先打印出来观察。
import pandas as pd #数据分析
import numpy as np #科学计算
from pandas import Series,DataFrame
data_train = pd.read_csv('/Users/lujiada/Documents/machine_learning/titanic/data/train.csv',engine = 'python',encoding='UTF-8')
data_test = pd.read_csv('/Users/lujiada/Documents/machine_learning/titanic/data/test.csv',engine = 'python',encoding='UTF-8')
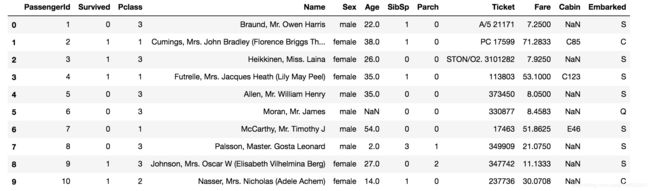
data_train[0:10]
- PassengerId 乘客编号,每位乘客唯一
- Survived 1为生还,2为不生还
- Pclass 船舱位等级
- Name 乘客名字
- Sex 性别
- Age 年龄
- SibSp 堂兄妹的人数
- Parch 父母或者儿女的人数
- Ticket 船票号码
- Fare 票价
- Cabin 客舱号码
- Embarked 登船港口
print(data_train.info())

打印出每列的信息发现,有些列的信息并不全,例如Cabin只有204个乘客有信息,其余都是缺失的,稍后要注意对其的处理。
print(data_train.describe())

describe函数打印了一些列的统计信息,比如均值、方差、最大最小值之类。这里只有7列是因为其余5列的类型是object,无法进行数值统计。注意这里的Age字段有些数据是缺失的,在统计的时候并不会包含缺失的数据。
从上边的统计可以看出,PassengerId就是每个乘客的编号,从1到891,这个字段很大几率对我们之后的分析是不起用处的。
根据Survived,成功获救的乘客大约是38%。
根据Pclass,三等舱的乘客最多。
根据Age,乘客平均年龄为29岁,有0岁的婴儿,也有80岁的老人。
只根据以上表格的话,比较难判断每个属性之间的关系,因此尝试画一些属性的分布,更好地理解他们的关系
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16,8))
fig.set(alpha=0.2) # 设定图表颜色alpha参数
plt.tick_params(labelsize=10)
plt.subplot2grid((2,3),(0,0)) # 在一张大图里分列几个小图
plt.tick_params(labelsize=20)
data_train.Survived.value_counts().plot(kind='bar')# plots a bar graph of those who surived vs those who did not.
plt.title(u"获救情况 (1为获救)",fontsize=15) # puts a title on our graph
plt.ylabel(u"人数",fontsize=15)
plt.subplot2grid((2,3),(0,1))
plt.tick_params(labelsize=20)
data_train.Pclass.value_counts().plot(kind="bar")
plt.ylabel(u"人数",fontsize=15)
plt.title(u"乘客等级分布",fontsize=15)
plt.subplot2grid((2,3),(0,2))
plt.tick_params(labelsize=20)
plt.scatter(data_train.Survived, data_train.Age)
plt.ylabel(u"年龄",fontsize=15) # sets the y axis lable
plt.grid(b=True, which='major', axis='y') # formats the grid line style of our graphs
plt.title(u"按年龄看获救分布 (1为获救)",fontsize=15)
plt.subplot2grid((2,3),(1,0), colspan=2)
plt.tick_params(labelsize=20)
data_train.Age[data_train.Pclass == 1].plot(kind='kde') # plots a kernel desnsity estimate of the subset of the 1st class passanges's age
data_train.Age[data_train.Pclass == 2].plot(kind='kde')
data_train.Age[data_train.Pclass == 3].plot(kind='kde')
plt.xlabel(u"年龄",fontsize=15)# plots an axis lable
plt.ylabel(u"密度",fontsize=15)
plt.title(u"各等级的乘客年龄分布",fontsize=15)
plt.legend((u'头等舱', u'2等舱',u'3等舱'),loc='best',fontsize=15) # sets our legend for our graph.
plt.subplot2grid((2,3),(1,2))
plt.tick_params(labelsize=20)
data_train.Embarked.value_counts().plot(kind='bar')
plt.title(u"各登船口岸上船人数",fontsize=15)
plt.ylabel(u"人数",fontsize=15)
plt.show()

由以上几张图可以看出,获救的人数大约为三分之一。
一等舱和二等舱的乘客差不多,三等舱乘客最多。
各个年龄段基本上都有获救的人数。
2等和3等舱的乘客基本是年龄40以下的居多,而头等舱乘客分布比较均匀。
绝大多数乘客都在S港口上船
分析了一下各个变量的分布,我们之后看一下各个变量与获救几率的关系
fig = plt.figure()
fig.set(alpha=0.2)
fig = plt.figure(figsize=(16,8))
plt.subplot2grid((2,3),(0,0))
plt.tick_params(labelsize=20)
data_to_plot=data_train.Pclass[data_train.Survived == 1].value_counts()/data_train.Pclass.value_counts()
data_to_plot.plot(kind='bar')
plt.title(u"各乘客等级获救概率",fontsize=15)
plt.xlabel(u"乘客等级",fontsize=15)
plt.ylabel(u"获救概率",fontsize=15)
plt.subplot2grid((2,3),(0,1))
plt.tick_params(labelsize=20)
data_to_plot=data_train.Sex[data_train.Survived == 1].value_counts()/data_train.Sex.value_counts()
data_to_plot.plot(kind='bar')
plt.title(u"男女获救概率",fontsize=15)
plt.xlabel(u"性别",fontsize=15)
plt.ylabel(u"获救概率",fontsize=15)
plt.subplot2grid((2,3),(0,2))
plt.tick_params(labelsize=20)
data_to_plot=data_train.Embarked[data_train.Survived == 1].value_counts()/data_train.Embarked.value_counts()
data_to_plot.plot(kind='bar')
plt.title(u"男女获救概率",fontsize=15)
plt.xlabel(u"性别",fontsize=15)
plt.ylabel(u"获救概率",fontsize=15)
plt.subplot2grid((2,3),(1,0))
plt.tick_params(labelsize=20)
data_to_plot=data_train.SibSp[data_train.Survived == 1].value_counts()/data_train.SibSp.value_counts()
data_to_plot.plot(kind='bar')
plt.title(u"不同亲戚数获救概率",fontsize=15)
plt.xlabel(u"亲戚数",fontsize=15)
plt.ylabel(u"获救概率",fontsize=15)
plt.subplot2grid((2,3),(1,1))
plt.tick_params(labelsize=20)
data_to_plot=data_train.Parch[data_train.Survived == 1].value_counts()/data_train.Parch.value_counts()
data_to_plot.plot(kind='bar')
plt.title(u"不同父母孩子数",fontsize=15)
plt.xlabel(u"父母孩子数",fontsize=15)
plt.ylabel(u"获救概率",fontsize=15)
plt.show()
由几张图可以看出:
- 舱位等级越高,获救概率越高。
- 女性的获救概率比男性高。
- 从C港口登船的乘客获救概率会稍高。
- 亲戚父母孩子数较少时,乘客获救的几率会较大
之后我们看看存活的情况和年龄的关系。
import seaborn as sns
g = sns.FacetGrid(data_train, col='Survived')
g.map(plt.hist, 'Age', bins=20)
从图可以看出,儿童(年龄10岁以下)的存活率是比较高的,20-40岁的青壮年的存活率不高。50岁以上的存活率大概为一半左右。
此图纵坐标应该画成存活率比较好,可惜的是对matplotlib和pandas的熟练度不够,未能成功。
从对年龄的分析可以得出以下结论:
- 年龄的分布对于存活率的影响很大。
- 年龄的记录并不全,可以想办法补全其空白。
- 年龄的记录较离散,可以将其分成几大块,有利于模型拟合。
数据清洗
接下来我们开始要对数据进行操作了。
首先,Ticket字段看上去是由没什么规律的数字组成的,因此将其去掉应该不会有太大影响。Cabin字段的无效值太多,因此也将其去掉。PassengerId是每位乘客的编号,也对预测没有影响,可以将其去掉
data_train = data_train.drop(["Cabin","Ticket","PassengerId"],axis=1)
data_test = data_test.drop(["Cabin","Ticket","PassengerId"],axis=1)
接下来我们需要将数据中非数字字段转化为数字字段,这样才能够用模型拟合。
性别字段
需要转化的字段有性别,还有Embarked登船港口,但是Embarked有空白的行,后边还需要针对空白行进行处理,因此我们先转化性别
data_train.loc[data_train['Sex']=='male','Sex']=0
data_test.loc[data_test['Sex']=='male','Sex']=0
data_train.loc[data_train['Sex']=='female','Sex']=1
data_test.loc[data_test['Sex']=='female','Sex']=1
data_train['Sex']=data_train['Sex'].astype(int)
data_test['Sex']=data_test['Sex'].astype(int)
data_train.head()
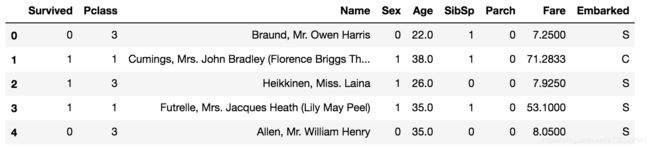
可以看到,性别Sex已经由male和female转化为0和1。
年龄字段
接下来针对年龄属性,对空白的行进行填充。一般来说,填充的方式有以下几种:
- 1.以总体数据的均值和方差作为样本,抽取正态分布的随机数。
- 2.结合其他列的特征来填取中位数(或正态分布随机数)
其中方法1可能会给样本带来噪声,因此选取方法2来填充年龄的空白。
grid = sns.FacetGrid(data_train, row='Pclass', col='Sex', size=3.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend(fontsize=5)
plt.show()
上图展示了Pclass和性别与年龄分布的关系,根据分析我们可以认为Pclass和性别与年龄的分布是有相关性的。因此我们将数据按Pclass和Sex分组,将年龄的空白分别填上对应类别的中位数。
combine=[data_train,data_test]
guess_ages = np.zeros((2,3))
for dataset in combine:
for i in range(0, 2):
for j in range(0, 3):
guess_df = dataset[(dataset['Sex'] == i) & \
(dataset['Pclass'] == j+1)]['Age'].dropna()
age_guess = guess_df.median()
guess_ages[i,j] = int( age_guess/0.5 + 0.5 ) * 0.5
for i in range(0, 2):
for j in range(0, 3):
dataset.loc[ (dataset.Age.isnull()) & (dataset.Sex == i) & (dataset.Pclass == j+1),\
'Age'] = guess_ages[i,j]
dataset['Age'] = dataset['Age'].astype(int)
年龄的空白填上之后,因为年龄的分布太分散,对模型的拟合不利,因此打算对不同年龄段进行分层处理。先看一下不同年龄段的生还概率
data_train['AgeBand'] = pd.cut(data_train['Age'],5)
data_train[['AgeBand','Survived']].groupby(['AgeBand'],as_index=False).mean()

可以看到不同年龄段对生还率还是有影响的。接下来根据不同年龄段,将离散的年龄值分段合并,并且移除data_train的"Age"字段
for dataset in combine:
dataset.loc[(dataset['Age']<16),'Age']=0
dataset.loc[(dataset['Age']>=16)&(dataset['Age']<32),'Age']=1
dataset.loc[(dataset['Age']>=32)&(dataset['Age']<48),'Age']=2
dataset.loc[(dataset['Age']>=48)&(dataset['Age']<64),'Age']=3
dataset.loc[(dataset['Age']>=64),'Age']=4
data_train=data_train.drop(['AgeBand'],axis=1)
combine=[data_train,data_test]
data_train.head()
家庭人数
Sibsp字段是亲戚朋友的人数,Parch的父母孩子的人数,因此其实可以创建一个家庭人数family size的字段,是这两者之和,然后可以扔掉Sibsp和Parch的字段。
for dataset in combine:
dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1
data_train=data_train.drop(['SibSp','Parch'],axis=1)
data_test=data_test.drop(['SibSp','Parch'],axis=1)
data_train[['FamilySize','Survived']].groupby(['FamilySize'],as_index=False).mean().sort_values(by='Survived',ascending=False)

可以看到,一家四口或一家三口获救的概率是比较高的,但是当家庭的人数过多时,生存概率就会下降。
Embark字段
freq_port = data_train.Embarked.dropna().mode()[0]
for dataset in combine:
dataset['Embarked']=dataset['Embarked'].fillna(freq_port)
data_train[['Embarked','Survived']].groupby('Embarked').mean().sort_values(by='Survived')

Embark字段有两个是空白的,简便起见,可以直接填写出现频率最高的那个港口名字。接下来将三个港口的名字以数字命名
for dataset in combine:
dataset['Embarked'] = dataset['Embarked'].map({'S':0,'Q':1,'C':2}).astype(int)
data_train.head()
Fare字段
data_test.info()
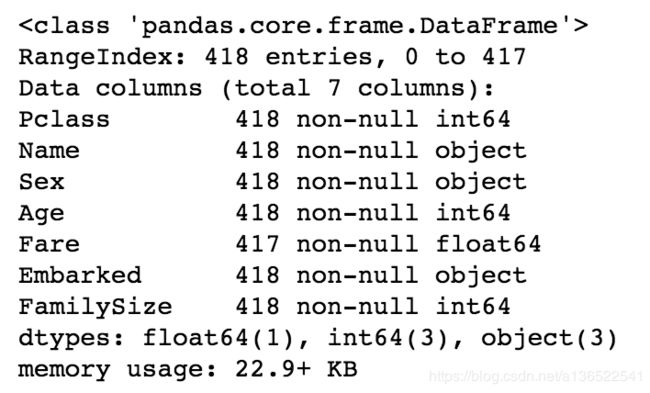
看到测试集中的Fare字段是有一个空白的,训练集没有空白,方便起见直接在Fare字段中填入中位数即可
data_test['Fare'].fillna(data_test['Fare'].dropna().median(),inplace=True)
data_train['FareBand'] = pd.qcut(data_train['Fare'], 4)
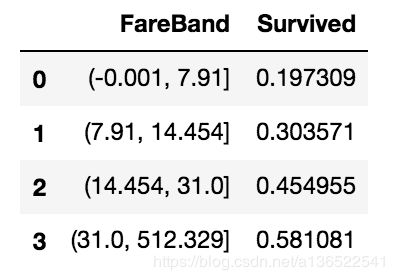
data_train[['FareBand','Survived']].groupby('FareBand',as_index=False).mean().sort_values(by='Survived')
将Fare分成数个区间后,可以看到票价越高,乘客的生还概率越高。类似对年龄段的处理,我们将Fare也进行分段。
combine=[data_train,data_test]
for dataset in combine:
dataset.loc[ dataset['Fare'] <= 7.91, 'Fare'] = 0
dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare'] = 2
dataset.loc[ dataset['Fare'] > 31, 'Fare'] = 3
dataset['Fare'] = dataset['Fare'].astype(int)
data_train.drop(['FareBand'],axis=1,inplace=True)
为了简洁起见Name字段我们也不要了,将其去掉之后剩下的列如下:
data_train.drop(['Name'],axis=1,inplace=True)
data_test.drop(['Name'],axis=1,inplace=True)
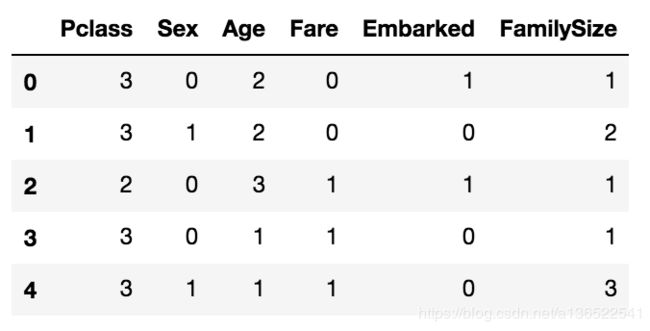
data_train.head()
经过以上处理,数据清洗完成,所有列的数据都变为整形且比较集中,下一步可以选择模型进行预测了。
我们的问题是分类问题,还是监督学习的问题。目标是获取乘客的信息并判断其能否生还,训练集有对应是否生还的标签,测试集没有。模型的种类有好多,包括:
- Logistic Regression
- KNN
- SVM
- Naive Bayes
- Decision Tree
- Random Forrest
由于测试数据集没有survived标签,需要在kaggle提交算法才能够获取准确的测试正确率,因此我们在训练集中划分一部分数据作为测试集使用
X_train = data_train[201:].drop("Survived",axis=1)
Y_train = data_train[201:]['Survived']
X_test = data_train[0:200].drop("Survived",axis=1)
Y_test = data_train[0:200]['Survived']
接下来我们测试一下几个算法的正确率
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
logreq = LogisticRegression()
logreq.fit(X_train,Y_train)
acc_log_train = round(logreq.score(X_train,Y_train)*100,2)
acc_log_test = round(logreq.score(X_test,Y_test)*100,2)
print(acc_log_train)#79.86
print(acc_log_test)#77.5
svc = SVC()
svc.fit(X_train, Y_train)
acc_svc_train = round(svc.score(X_train, Y_train) * 100, 2)
acc_svc_test = round(svc.score(X_test, Y_test) * 100, 2)
print(acc_svc_train)#82.61
print(acc_svc_test)#84
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, Y_train)
acc_knn_train = round(knn.score(X_train, Y_train) * 100, 2)
acc_knn_test = round(knn.score(X_test, Y_test) * 100, 2)
print(acc_knn_train)#85.51
print(acc_knn_test)#78.5
sgd = SGDClassifier()
sgd.fit(X_train, Y_train)
acc_sgd_train = round(sgd.score(X_train, Y_train) * 100, 2)
acc_sgd_test = round(sgd.score(X_test, Y_test) * 100, 2)
print(acc_sgd_train)#78.99
print(acc_sgd_test)#72
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
acc_decision_tree_train = round(decision_tree.score(X_train, Y_train) * 100, 2)
acc_decision_tree_test = round(decision_tree.score(X_test, Y_test) * 100, 2)
print(acc_decision_tree_train)#88.26
print(acc_decision_tree_test)#79
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
acc_random_forest_train = round(random_forest.score(X_train, Y_train) * 100, 2)
acc_random_forest_test = round(random_forest.score(X_test, Y_test) * 100, 2)
print(acc_random_forest_train)#88.26
print(acc_random_forest_test)#78
经过对比发现,各种算法的性能没有十分明显的差异,对于测试集,最终的正确率基本都能够保持在70-80%左右。
总结
本文结合了kaggle的入手项目,Titanic号上乘客的获救情况分析,讲述了一下数据处理的各种方式。包括了连续的数据离散化,缺失数据的处理,非数字数据转化为数字等。
接下来的文章将会讲述一下各种机器学习算法的原理,以及使用方法。
本文代码在这里