机器学习笔记（二十三）：算法精准率、召回率

凌云时刻 · 技术

导读：‍‍‍‍‍‍‍‍‍机器学习算法中有一个重要环节就是评判算法的好坏，我们在之间的笔记中讲过多种评价回归算法的评测标准，比如均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）、    （R Squared）。但是在分类问题中我们一直使用分类准确度这一个指标，也就是预测对分类的样本数量除以总预测样本数量。但是这个方法存在很大的一个缺陷，所以这篇笔记主要介绍评价分类问题的方式方法。‍‍‍‍‍‍‍‍

作者 | 计缘

来源 | 凌云时刻（微信号：linuxpk）

极度偏斜数据（Skewed Data）

为什么说分类准确度这个指标存在很大的一个缺陷呢。举个例子，假设有一个癌症预测系统，输入体检信息，判断是否患有癌症。我们知道世界上相对于其他病症，患癌症的比例还是很小，如果癌症产生的概率只有0.1%，那么有99.9%的人都不会患有癌症。这就意味着，就算癌症预测系统什么都不做，但凡有体检信息输入，就给出没有患癌症的结果，那准确率也是达到了99.9%。那此时这个分类准确度是真实的吗？所以当样本数据或领域的实际情况存在数据极度偏斜的时候，只使用分类准确度这个指标是远远不够的。

混淆矩阵（Confusion Matrix）

这一节介绍一个能进一步分析分类结果的工具，混淆矩阵。

上面这个表针对二分类问题，所有将类别就分为两类0和1，0表示Negative，类似医院上的阴性，1表示Positive，类似医学上的阳性。行代表真实值，列代表预测值。

如上图所示：

• (0, 0)格子真实值和预测值都为0，称为预测Negative正确，记作True Negative，简写为TN。

• (0, 1)格子真实值为0，但预测值为1，称为预测Positive错误，记作False Positive，简写为FP。

• (1, 0)格子真实值为1， 但预测值为0，称为预测Negative错误，记作False Negative，简写为FN。

• (1, 1)格子真实值和预测值都为1，称为预测Positive正确，记作True Positive，简写为TP。

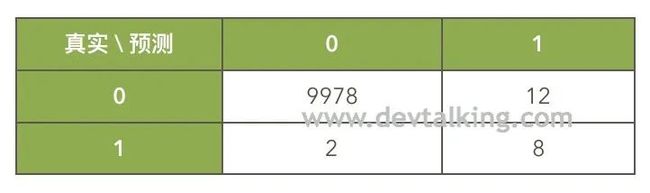
以上这个表格就叫做混淆矩阵。举个例子，如果对10000个人预测他们是否患癌症，通过混淆矩阵表示出的真实情况就是：

解读一下：

• 没有患癌症，系统也预测出没有患癌症的人为9978人（TN）。

• 没有患癌症，但系统预测出患癌症的人为12人（FP）。

• 患有癌症，但系统预测出没有患癌症的人为2人（FN）。

• 患有癌症，系统也预测出患有癌症的人为8人（TP）。

精准率（Presicion）

分类问题的精准率是建立在混淆矩阵的基础上的，那么精准率的公式为：

   

还是以预测10000人是否患癌症的例子来说明：

这个例子中，预测患癌的精准率是8 / (8+12) = 40%，既真实患癌并预测出患癌的人数在所有预测出患癌人数中的占比。

召回率（Recall）

分类问题的召回率同样也是建立在混淆矩阵的基础上的，召回率的公式为：

   

以预测10000人是否患癌症的例子来说明：

这个例子中，预测患癌的召回率是8 / (8+2) = 80%，既真实患癌并预测出患癌的人数在真实患癌总人数中的占比。

我们之前解释过分类准确度存在的缺陷，那么在这个例子中，我们通过混淆矩阵来直观的看一下这个缺陷。我们的前提是10000个人中患癌的人占比为0.1%，那么健康的人占比为99%，在这种情况下，有极大的可能出现分类准确度为99.9%，但是实际上一个患癌的人都没有预测出来。

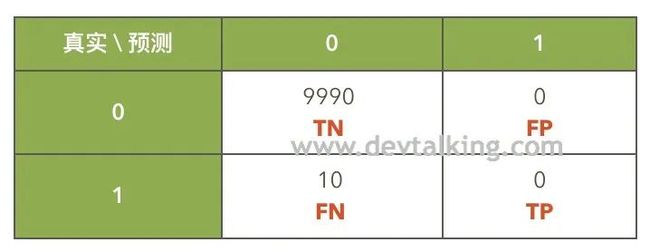
上面这个混淆矩阵就满足我们假定的这个情况，现在来看看分类准确度、精准率和召回率分别是多少：

• 分类准确度：9990 / 10000 = 99.9%

• 精准率：0 / (0+0)，无意义，既为0

• 召回率：0 / (10 +0) = 0

现在可以很清晰的看出分类准确度存在的缺陷和混淆矩阵对分类评价的重要性了。

实现精准率和召回率

有了上面的定义，下面我们来实现一下混淆矩阵、精准率和召回率。首先我们使用手写数据作为样本数据，因为手写数据是多分类问题，所以还要对其做一下处理，转换为二分类问题，同时让其数据产生极度偏差：

 

import numpy as np from sklearn import datasets # 使用手写数据作为样本数据 digits = datasets.load_digits() X = digits.data y = digits.target.copy() # 将多分类问题转换为二分类问题，同时让样本数据产生极度偏斜， # 也就是我们关注的数据占总数据的1/9 y[digits.target == 9] = 1 y[digits.target != 9] = 0

 

样本数据构建好后，我们先使用逻辑回归训练出模型，先看看分类准确度指标：

 

from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666) from sklearn.linear_model import LogisticRegression log_reg = LogisticRegression() log_reg.fit(X_train, y_train) log_reg.score(X_test, y_test) # 结果 0.97555555555555551

 

下面我们来逐个实现混淆矩阵中的TN、FP、FN、TP：

 

# 使用逻辑回归模型计算测试特征数据的预测目标值 y_predict = log_reg.predict(X_test) def TN(y_true, y_predict): assert len(y_true) == len(y_predict) return np.sum((y_true == 0) & (y_predict == 0)) TN(y_test, y_predict) # 结果 403 def FP(y_true, y_predict): assert len(y_true) == len(y_predict) return np.sum((y_true == 0) & (y_predict == 1)) FP(y_test, y_predict) # 结果 2 def FN(y_true, y_predict): assert len(y_true) == len(y_predict) return np.sum((y_true == 1) & (y_predict == 0)) FN(y_test, y_predict) # 结果 9 def TP(y_true, y_predict): assert len(y_true) == len(y_predict) return np.sum((y_true == 1) & (y_predict == 1)) TP(y_test, y_predict) # 结果 36 def confusion_matrix(y_true, y_predict): return np.array([ [TN(y_test, y_predict), FP(y_test, y_predict)], [FN(y_test, y_predict), TP(y_test, y_predict)] ]) confusion_matrix(y_test, y_predict) # 结果 array([[403, 2], [ 9, 36]])

我们通过上面的混淆矩阵来分析一下：

• y被拆分后的测试数据量y_test为450，混淆矩阵中的四个熟总和为450。

• 真值为0，但预测值为1有2个。

• 真值为1，但预测值为0有9个。

• 真值为1，预测值也为1有36个。

也就是全部预测对的有439个，分类准确度为439 / 450 = 97.56%。下面来看看如何实现精准率和召回率：

 

# 精准率 def precision_score(y_true, y_predict): tp = TP(y_test, y_predict) fp = FP(y_test, y_predict) try: return tp / (tp + fp) # 避免分母为0报错 except: return 0.0 precision_score(y_test, y_predict) # 结果 0.94736842105263153 # 召回率 def recall_score(y_true, y_predict): tp = TP(y_test, y_predict) fn = FN(y_test, y_predict) try: return tp / (tp + fn) # 避免分母为0报错 except: return 0.0 recall_score(y_test, y_predict) # 结果 0.80000000000000004

 

以上是我们根据定义自己实现的混淆矩阵和精准率、召回率。下面来看看Scikit Learn中封装的它们：

 

# Scikit Learn 中的混淆矩阵 from sklearn.metrics import confusion_matrix confusion_matrix(y_test, y_predict) # 结果 array([[403, 2], [ 9, 36]]) # Scikit Learn中的精准率 from sklearn.metrics import precision_score precision_score(y_test, y_predict) # 结果 0.94736842105263153 # Scikit Learn中的召回率 from sklearn.metrics import recall_score recall_score(y_test, y_predict) # 结果 0.80000000000000004

F1 Score

上一节介绍了精准率和召回率，那么如果在一个指标好，一个指标不好的情况下，如何确定一个模型的好坏呢？这就要分情况而视了。像预测股市的系统中，一般主要关注精准率，也就是关注在预测出要涨的股票中的准确程度。那么像医疗相关的系统中就会主要关注召回率，也就是关注在真正患病的人群中预测出的准确程度。如果两个指标都要关注的话，就要引入第三个指标了，那就是F1 Score。

 F1 Score定义

我们看多个数的综合情况时，一般情况都会求这些数的平均值，称为算数平均值。但是在机器学习中，算数平均值是有缺陷的，因为它们是求和然后取平均，如果大多数数很大，个别几个数很小的话，平均值并不会被拉下来，但作为机器学习模型的评测标准，可能只要有一个指标不好，那么整个模型就不是一个好的模型。所以我们得使用调和平均值：

   

最后换算下来的最终F1 Score公式为：

   

调和平均值的最大特点就是，精准率和召回率只要有一个比较小的话，整个F1 Score也会被拉下来，既避免了算数平均值在评估机器学习算法分类模型时的缺陷。

 实现F1 Score

我们知道了F1 Score的定义后，实现它就很容易了：

import numpy as np def f1_score(precision, recall): try: return 2 * precision * recall / (precision + recall) except: return 0.0 precision = 0.5 recall = 0.5 f1_score(precision, recall) # 结果 0.5 precision = 0.1 recall = 0.9 f1_score(precision, recall) # 结果 0.18000000000000002

从结果可以看到，当两个指标相等时，F1的值也和它们相等。当其中一个指标比较小时，F1的值也会被拉的比较小。

 Scikit Learn 中的 F1 Score

Scikit Learn中也封装了F1 Score，但是它封装时传的参数和我们实现的不太一样，它只需要传入真值和预测值既可，精准率和召回率是在函数中计算的：

 

from sklearn.metrics import f1_score f1_score(y_test, y_predict) # 结果 0.86746987951807231

从结果可以看到上一小节中的手写数据的例子，虽然分类准确度达到了97.56%，但是F1 Score只有86.75%，而这个86.75%才是更能真正反应模型好坏程度的指标。

  

 

END

往期精彩文章回顾

机器学习笔记（二十二）：逻辑回归中使用模型正则化

机器学习笔记（二十一）：决策边界

机器学习笔记（二十）：逻辑回归(2)

机器学习笔记（十九）：逻辑回归

机器学习笔记（十八）：模型正则化

机器学习笔记（十七）：交叉验证

机器学习笔记（十六）：多项式回归、拟合程度、模型泛化

机器学习笔记（十五）：人脸识别

机器学习笔记（十四）：主成分分析法（PCA）(2)

机器学习笔记（十三）：主成分分析法（PCA）

长按扫描二维码关注凌云时刻

每日收获前沿技术与科技洞见