机器学习笔记（二十五）：支撑向量机（SVM）

凌云时刻 · 技术

导读：这一篇笔记主要讲机器学习算法中一个重要的分类算法，支撑向量机（Support Vector Machine）。它背后有严格的数学理论和统计学理论支撑的，这里我们只对它的原理和应用做以介绍，更深层次的数学理论有兴趣可以查阅其他资料。

作者 | 计缘

来源 | 凌云时刻（微信号：linuxpk）

什么是SVM

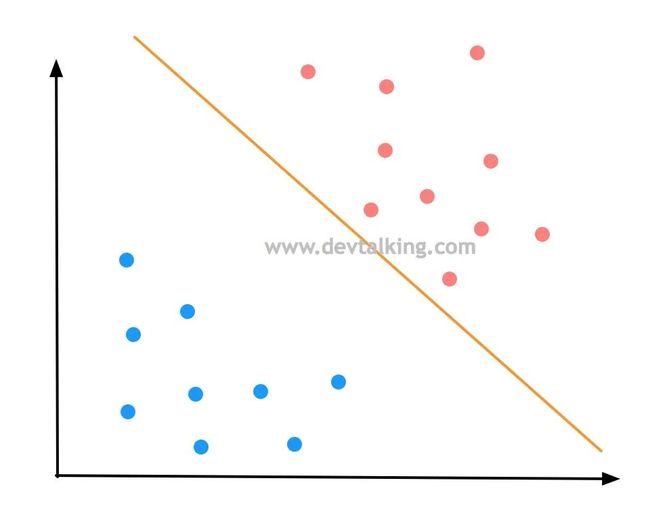
上面的图展示的是一个二分类问题，在逻辑回归的笔记中，我们知道了决策边界，图中橘黄色的直线就是决策边界，它看似很好的将样本数据的不同分类区分开了。我们在多项式回归的笔记中，讲过模型泛化的问题，一个模型的好坏程度很大程度上是体现了模型泛化能力的好坏，也就是对未知样本的预测能力。

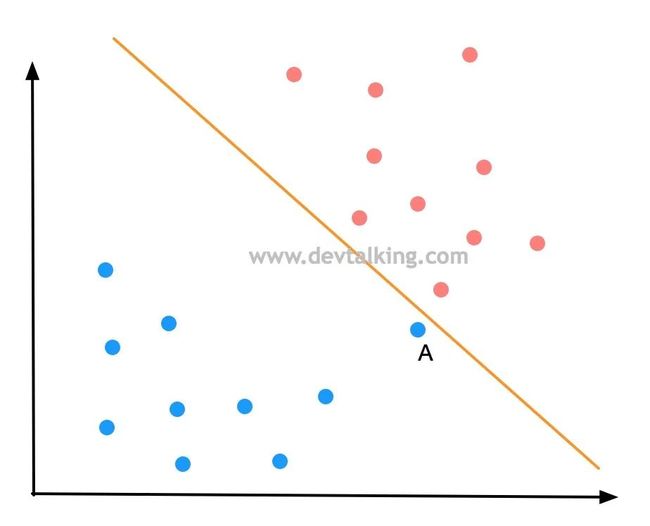
如果新来一个样本数据A，按照决策边界划分它是被分为了蓝色分类，可事实真的是如此吗，因为点A和红色分类的点非常近，很有可能点A是属于红色分类的。所以上图中的决策边界可能并不是最优的，那最优的决策边界应该是什么样的呢？

上面的决策边界之所以有缺陷，是因为它和红色类别的点太近了，当然肯定也不能和蓝色的点太近了，所以我们希望这条决策边界离红色分类和蓝色分类都尽可能的远，才能很好的避免上面出现的问题。

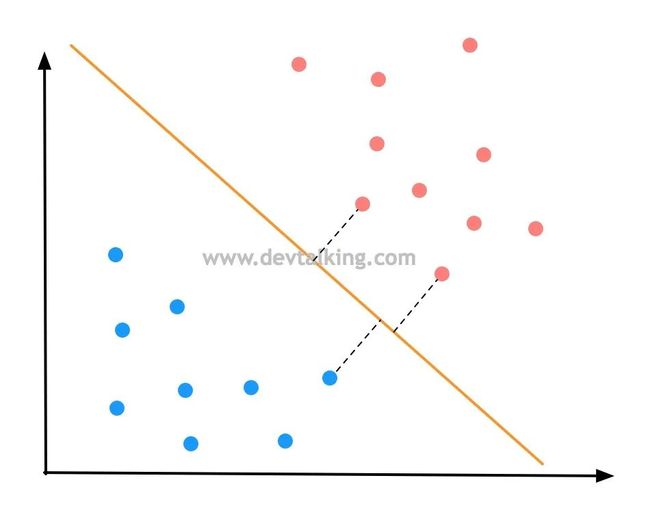
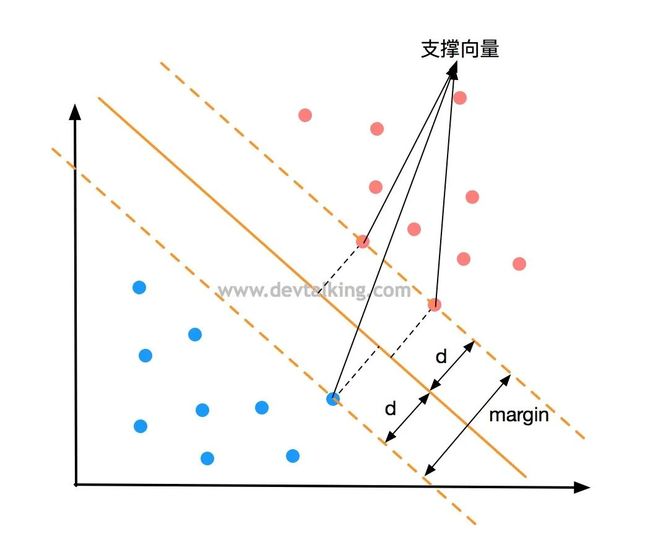
想要决策边界离红蓝两个分类都尽可能的远，也就是红蓝分类两边离决策边界最近的点的距离要远，并且两边的点到决策边界的距离要相等，这才说明决策边界是不偏不倚的，如上图所示。

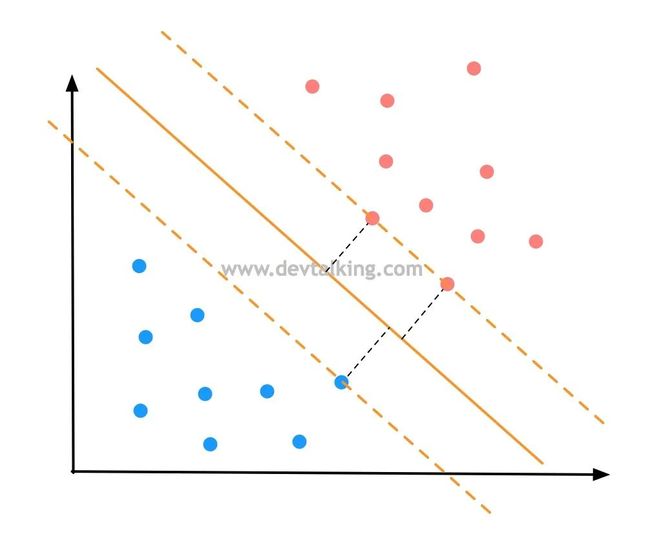
过红蓝两边离决策边界最近的点画两条直线，并且平行于决策边界，那么就确定了一个区域，在这个区域内不应该再有任何数据点出现。那么SVM就是尝试寻找这个区域中间那条最优的决策边界。这个区域边界上的点称为支撑向量，换句话说，是支撑向量定义出了这个区域，那么最优的决策边界也是由支撑向量决定的，这也是支撑向量机这个名称的由来。

如上图所示，由支撑向量确定的区域之间的距离称为Margin。那么SVM要做的事情就是最大化Margin，既将问题转化为了求最优解的问题。

以上对SVM的解释是基于线性可分问题的基础上，也就是能确确实实找到一条直线作为决策边界，这种问题称为Hard Margin SVM，但是很多真实的情况是线性不可分的，这类问题称为Soft Margin SVM，这两类问题都是支撑向量机可以处理的，但基础还是Hard Margin SVM。

SVM背后的最优化问题

从上面的示例图上可以看出，Margin其实就是二倍的‍‍   ，‍‍   ‍‍是‍‍支撑向量到决策边界的距离，那么求Margin的最大值就是求   ‍‍的最大值。

 点到直线的距离

在解析几何中我们学过，假设有条直线定义为‍‍   ‍‍，有一点的‍‍坐标为   ，那‍‍么该点到该条直线的距离为：

   

那么果扩展到高维空间中，点到直线的距离为：

   

   、   、   可以看作样本数据的特征，而   、   、   可以看作是特征系数。那么上面的公式可以写为：

   

将   向量化后，公式可写为：

   

再根据向量的模的公式   ，上面的公式可继续转换为：

   

   为特征系数向量，   为特征向量。

 限定条件的最优化问题

有了上面的公式后，我们就可以假定决策边界直线的公式为   ，支撑向量到它的距离为   。那么除了支撑向量以外的点到决策边界的距离都应该大于   。

我们将上图中红色点定义为1类别，蓝色点定义为-1类别，那么就有：

   

既任意类别为1的红色点距离决策边界的距离要大于等于   。任意类别为-1的蓝色点距离决策边界的距离要小于等于   。将上面的两个公式左右分别除以   得：

    

下面来分析上面的公式，   是一个标量，   也是一个标量，所以分母   也是一个标量。那么对于分子中的向量   除以一个标量仍然是一个向量，可以记为   。分子中的标量   除以一个标量自然也是一个标量，记为   。所以上面的公式又可以转换为：

   

这样也就得出了由红色点支撑向量构成的直线公式为：

   

由蓝色点支撑向量构成的直线公式为：

   

在逻辑回归的笔记中我们知道通过一个技巧可以将上面两个公式通过一个公式表示出来，既公式左右两边都乘以   ，得：

   

为了书写方便，我们就将   和   命名为   和   。所以最终我们希望的是对于所有的样本数据点都满足下面的公式：

   

那么上面这个公式就是SVM中最优化目标函数的限定条件，标识为   （Such That）。

 目标函数

在这一节开始时我们就很明确我们的目标是求   的最大值，即：

   

根据之前的推导我们知道，无论是红色点的支撑向量，还是蓝色点的支撑向量构成的直线公式取绝对值后都为1，所以我们的目标函数又可以写为：

 

即：

 

为了方便求导，我们再将其转换一下，最终SVM的目标函数为：

   

那么最后SVM的最优化问题的两个函数为：

   

也就是在   这个限定条件下 ，求目标函数   的最优解。

这就和我们之前学习过的算法不一样了，之前不论是线性回归还是逻辑回归，在求最优化问题时都是求全局最优化问题，也就是没有限定条件的目标函数最优解问题，这类问题对目标函数求导让他等于0，然后相应的极值点就是最大值或最小值的位置。而SVM是有条件的最优化问题，此时求目标函数的极值就复杂了很多，这里就不对求解过程做详细阐述了。

  

 

END

往期精彩文章回顾

机器学习笔记（二十四）：召回率、混淆矩阵

机器学习笔记（二十三）：算法精准率、召回率

机器学习笔记（二十二）：逻辑回归中使用模型正则化

机器学习笔记（二十一）：决策边界

机器学习笔记（二十）：逻辑回归(2)

机器学习笔记（十九）：逻辑回归

机器学习笔记（十八）：模型正则化

机器学习笔记（十七）：交叉验证

机器学习笔记（十六）：多项式回归、拟合程度、模型泛化

机器学习笔记（十五）：人脸识别

长按扫描二维码关注凌云时刻

每日收获前沿技术与科技洞见