群体智能优化算法之细菌觅食优化算法(Bacterial Foraging Optimization Algorithm，BFOA)

获取更多资讯，赶快关注上面的公众号吧！

第十四章 细菌觅食优化算法

14.1 介绍

Passino等人[1]于2002年通过模拟人体内大肠杆菌的觅食行为，提出了一种新型智能优化算法：细菌觅食优化算法(Bacterial Foraging Optimization Algorithm，BFOA)。细菌觅食优化算法通过细菌群体之间的竞争与协作实现优化，是一种基于细菌群体的搜索技术。在群智能算法中，GA、ACO、PSO、AFSA都是基于高等生物作为启发对象，而BFOA算法则是模拟微生物的行为而形成的一种较新的优化方法。

14.2 BFOA的基本原理与流程

BFOA算法是一种全局随机搜索的算法，其具有简单、收敛速度快，并且在优化过程中无需优化对象的梯度信息的特点。BFOA模拟细菌群体的过程包括趋向性（Chemotaxis）、复制（Reproduction）、迁徙（Elimination dispersal）.三个步骤。

14.2.1 趋向性操作

细菌向有利于自身环境的区域移动称为趋向运动，其中，一次趋向性操作包括翻转运动和游动运动。细菌向任意方向移动单位步长称为旋转运动；细菌沿着上一步的运动放向移动单位步长称为游动运动。通常，细菌在环境差的区域（如：有毒区域）会较频繁地旋转，在环境好的区域（如：食物丰富的区域）会较多地游动。大肠杆菌的整个生命周期就是在游动和旋转这两种基本运动之间进行变换，游动和旋转的目的是寻找食物并避开有毒物质。

设细菌种群大小为S，细菌所在的位置标示问题的一个候选解，细菌i的信息用D维向量标示为$${\theta }^i=\left[{\theta }_1^i,{\theta }_2^i,\cdots ,{\theta }_D^i\right]$$，i=1,2,…,S，θⁱ(j,k,l)表示细菌i在第j次趋向性操作、第k次复制操作和第l次迁徙操作后的位置。细菌i通过式（1）更新其每一步趋向性操作后的位置。
$${\theta }^i(j+1,k,l)={\theta }^i(j,k,l)+C(i)\Phi (j)\text{\hspace{1em}(1)}$$

其中C(i)>0表示向前游动的步长，Φ(j)表示旋转后随机选择的单位方向向量。如果在θⁱ(j+1,k,l)处的适应度优于θⁱ(j+1,k,l)处，则保持Φ不变继续在该方向游动，直至找到适应度最佳的位置或达到设定的趋向性次数；否则产生新的Φ，进行下一次旋转运动。
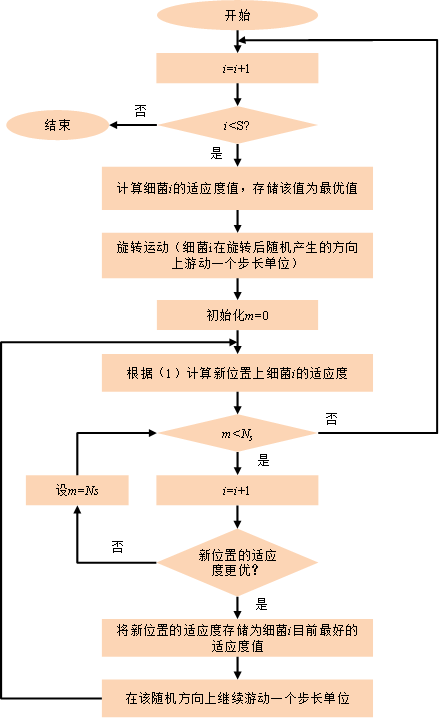
设N_s是趋向性操作中在一个方向上前进的最大步数（用m进行索引），初始时该值为0，BFOA趋向性操作的流程图如图1所示。

图1 趋向性操作流程图

目前的讨论主要是针对不考虑细菌间相互吸引的情况，实际上每个细菌个体除按照自己的方式搜索食物外，还收到种群中其他个体发出的吸引力信号，即个体会游向种群中心。

第i_th个细菌的细菌间吸引力用$$J_{cc}^i\left(\theta ,{\theta }^i(j,k,l)\right),i=1,2,\dots ,S$$表示，d_attract=0.1表示细菌释放的吸引量多少（深度），w_attract=0.2用于度量吸引信号的宽度（量化化学物质的扩散率）。

同时也会收到附近个体发出的排斥力信号，以保持个体与个体之间的安全距离，因为细菌消耗附近的营养物质，在物理上不可能在同一位置有两个细菌，对此，令h_repellant=d_attract表示排斥力的高度（排斥影响程度），w_repellant=10度量了排斥力的宽度。
令J_cc(θ,P(j,k,l))表示同时考虑了细菌间吸引力和排斥力的综合影响，其计算公式如（2）。

$$\begin{array}{rl}{J}_{cc}(\theta ,P(j,k,l))=& \sum _{i=1}^S{J}_{c\epsilon }^i\left(\theta ,{\theta }^i(j,k,l)\right)\\ =& \sum _{i=1}^s\left[-d_{\text{atact }}\exp \left(-w_{\text{attact }}\sum _{m=1}^p{\left({\theta }_m-{\theta }_m^i\right)}^2\right)\right]\\ & +\sum _{i=1}^s\left[h_{\text{repenatint }}\exp \left(-w_{\text{repelinat }}\sum _{m=1}^p{\left({\theta }_m-{\theta }_m^i\right)}^2\right)\right]\end{array}\text{\hspace{1em}(2)}$$

其中P(j,k,l)表示在第j次趋向性操作、第k次复制操作和第l次迁徙操作后，种群S中每个细菌的位置，θ=[θ₁,…,θ_D]^T是优化域上的一个点，θⁱ_m是第i个细菌位置θⁱ的第m个元素。
$$P(j,k,l)=\left\{{\theta }^i(j,k,l)|i=1,2,\dots ,S\right\}\text{\hspace{1em}(3)}$$

因此考虑上述两个因素对细菌行为的影响，执行一次趋向性操作后细菌i的新适应度函数值为：

$$J(i,j+1,k,l)=J(i,j,k,l)+J_{cc}\left({\theta }^i(j+1,k,l),P(j+1,k,l)\right)\text{\hspace{1em}(4)}$$

这样这些细胞会试图寻找营养物质，避免有毒物质，同时试图向其他细胞移动，但又不会靠得太近。

14.2.2 复制操作

生物进化过程的规律是优胜劣汰。经过一段时间的食物搜索过程后，部分寻找食物能力弱的细菌会被自然淘汰掉，为了维持种群规模，剩余的细菌会进行繁殖。在细菌觅食优化算法中将这种现象称为复制行为（Reproduction）。

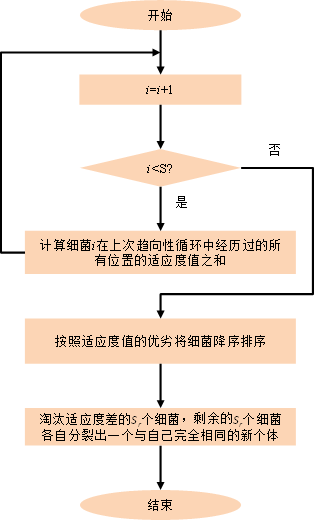
在BFOA中，经过复制操作后算法的种群大小不变。设淘汰掉的细菌个数为S_r＝S/2，首先按照细菌位置的优劣排序，然后把排在后面的S_r个细菌淘汰掉，剩余的Sr个细菌进行自我复制，各自生成一个与自己完全相同的新个体，即生成的新个体与原个体有相同的位置，或者说具有相同的觅食能力。初始时设i=0，复制操作流程图如图2所示。

图2 复制操作流程图

14.2.3 迁徙操作

细菌个体生活的局部区域可能会突然发生变化（如：温度的突然升高）或者逐渐变化（如：食物的消耗），这样可能会导致生活在这个局部区域的细菌种群集体死亡，或者集体迁徙到一个新的局部区域。在细菌觅食优化算法中将这种现象称为迁徙行为（Elimination-dispersal）。

迁徙操作以一定概率发生，给定概率p_ed，如果种群中的某个细菌个体满足迁徙发生的概率，则这个细菌个体灭亡，并随机地在解空间的任意位置生成一个新个体，这个新个体与灭亡的个体可能具有不同的位置，即不同的觅食能力。迁徙操作随机生成的这个新个体可能更靠近全局最优解，这样更有利于趋向性操作跳出局部最优解和寻找全局最优解。
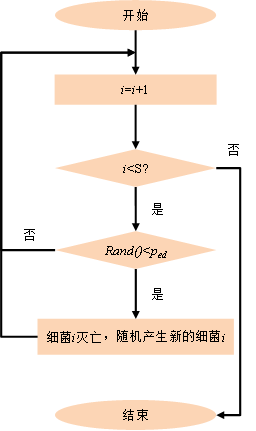
初始时设i=0，rand()是[0,1]区间上均匀分布的随机数，迁徙操作流程如图3所示。

图3 迁徙操作流程图

14.3 BOFA算法

参考文献

1. Passino, K.M., Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Systems Magazine, 2002. 22(3): p. 52-67.